服装矩形样片组合优化模型及其求解算法

王 姝，金福江

(华侨大学信息科学与工程学院，福建 厦门 361021)

面料利用率直接影响服装企业的生产成本和生产效率，因此服装排料技术是服装生产的关键。从数学计算复杂性理论来看，优化排料问题属于具有最高计算复杂性的NPC类问题［1］，这类问题的求解时间与问题的规模呈指数级关系增长［2－3］，至今还没有找到解决该问题的有效方法。目前，服装企业中应用较多的排料方法还是传统的人工排料。即在反复多次摆放后，一般能达到较高的排料率，但通常排料周期较长，效率低，修改难度大。随着计算机的广泛应用，服装CAD排料系统被运用于服装排料中，虽然能使排料完全实现自动化，但缺乏相应的数学模型和优化算法，达不到最优排料的要求。

针对服装排料问题，国内外学者提出了很多算法。ALBANO在树搜索的基础上加入启发式的搜索技术，把样片的二维最优布局问题转化为在一个状态空间寻找一条最优路径的问题，得到了一个近似优化的排料方案［4］，启发式算法提高了搜索效率，放宽了对计算结果与最优解偏离程度的限制，求出的不一定是最优解。ADAMOWICZ的算法是在矩形布局阶段采用了矩形包络法［5］，将不规则图形简化为矩形，简化算法的复杂度。HAIMS的规划方法适用于矩形排料，待排部件数量不受限制，在每一步都将矩形部件放在料板的一个角上［6］。GILMORE和GOMORY用线性规划方法和背包算法研究了矩形图形的二维排料问题［7］，但是不适用于不规则多边形的直接排料。国内的学者也做了大量的研究［8－12］，但在以往的研究中，把服装排料问题的重点放在算法上，对实际排料的模型研究成果较少。笔者运用矩形包络法，先将服装裁片通过组合优化，得到相应的矩形件，再研究服装最优排料的数学模型，弥补了服装排料理论研究的不足。

1 矩形样片服装排料问题

笔者对服装排料建模做如下假设:

(1)在定宽定长的面料上，每批服装的所有样片均参与自动排料。

(2)矩形样片长宽一定，且数量不限。

(3)暂且不考虑实际排料中面料的色差、纹理等条件。

矩形样片服装排料问题的描述如下:

(1)一系列数量不限的矩形样片为Pn，这里n为不同尺寸矩形的种类数，矩形样片的长度为ai(i=1，2，…，n)，矩形样片的宽度为 bi，矩形样片沿宽度方向的矢量为di，矩形样片的面积为si。

(2)设逻辑变量为γi，面料沿长度方向的矢量为d。γi=did，γi=0表示矩形Pn为横排，即Pn的长度方向沿面料长度方向排列，γi=1表示Pn为竖排，即Pn的长度方向沿面料宽度方向排列。

(3)设面料利用率为η，在幅宽为W，长度为L的面料P上排放矩形样片Pn，η=∑si/(WL)，因面料面积为WL不变，当所有所排矩形面积∑si最大时，服装面料利用率η最大。

对于排放任意矩形样片Pn，为不超出面料范围，则每一列排放的矩形样片的长度或宽度的总和不能超过面料的幅宽，每一行排放的矩形样片的长度或宽度的总和不能超过面料的长度。

2 矩形样片混合排料的建模

当所排的矩形样片满足γi=0或1，即所排矩形样片中包含有既可横排(γi=0)也可竖排(γi=1)的矩形样片时，混合排料建模分析如下:

设Sj为第j列所有矩形件的面积和，Wj为第j列所有矩形件的宽度或长度和，Lj为第j列所有矩形件中长度或宽度的最大值，kij为逻辑变量，kij=1为第i种矩形件排列于第j列中，kij=0为第i种矩形件未排列于第j列中。

对于第j列，每类矩形件的个数分别为xij(0≤xij≤X且xij∈Z)，则矩形样片面积和为:

矩形样片宽度和为:

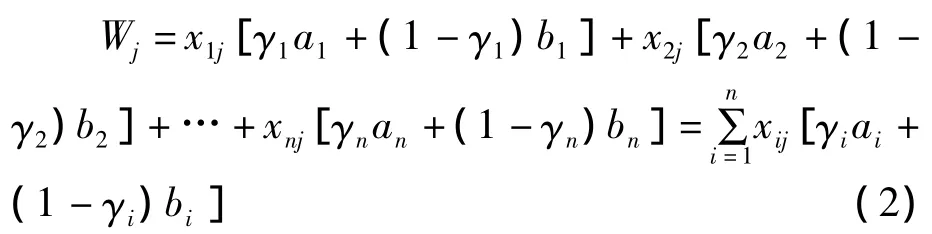
矩形样片长度和为:

其中，kij为逻辑变量，kij=1为第i种矩形件排列于第j列，kij=0为第i种矩形件未排列于第j列，即则对于整块面料，其总面积和为:

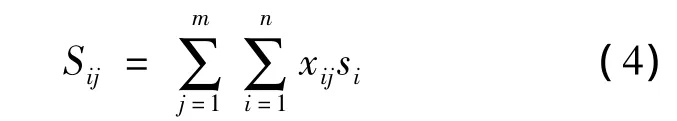
1≤m≤M，M=int(L/f)，且 m∈Z

f=min{［(1 －γ1)a1+γ1b1］，…，［(1 －γn)an+ γnbn］}

总宽度为:

总长度为:

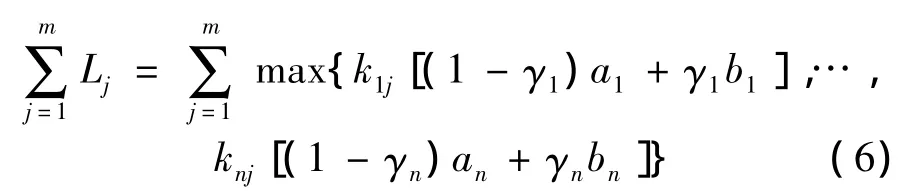
其中

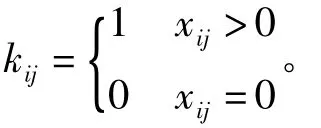
综上所述，得混合排料方式(γi=0或1)下，服装排料的组合优化模型为:

其中，式(8)为面积约束;式(9)为面料宽度约束;式(10)为面料长度约束;矩形样片排列的总列数m满足1≤m≤M，M=int(L/f)，f=min{［(1 － γ1)a1+ γ1b1］，［(1 － γ2)a2+ γ2b2］，…，［(1 －γn)an+γnbn］}且 m∈Z，xij为第 j列第 i种矩形样片的个数，0≤xij≤X，X=int(W/c)，c=min{［γ1a1+(1 － γ1)b1］，［γ2a2+(1 － γ2)b2］，…，［γnan+(1 － γn)bn］}且 xij∈Z，kij为逻辑变量，kij=1为第i种矩形件排列于第j列，kij=0为第i种矩形件未排列于第j列。

3 混合排料的组合优化算法

n种矩形样片的排料方式共有2n种。通过对2n种情况进行分类建模讨论，得出最佳排料方案。(γ1，γ2，…，γn)为矩形样片的排列方式，γ =0为矩形样片横排，γ=1为矩形样片竖排。计算步骤如下:

(1)将(γ1，γ2，…，γn)的某种情况代入 M=int(L/f)，f=min{［(1 －γ1)a1+γ1b1］，…，［(1 －γn)an+γnbn］}和 X=int(W/c)，c=min{［γ1a1+(1 － γ1)b1］，［γ2a2+(1 － γ2)b2］，…，［γnan+(1 －γn)bn］}中，求解出 M、f、X、c。

(2)将求解出的M、f、X、c代入服装排料的组合优化模型中，得到具体的模型。

(3)通过式(9)求解出满足条件的xij和mi(xij为第j列第i种矩形样片的个数，mi为矩形样片排料的总个数)。

(4)通过式(8)算出面料的使用面积，比较可得最大的面料利用率，以及面料利用率最大时的xij和mi。返回步骤(1)，直到讨论完所有情况。

(5)通过比较各种情况的面料利用率，确定最佳排料方案，最后得到排料图。

4 混合排料模型的验证

以4种类型的矩形样片为例，来说明混合排列方式下的排料模型。设定面料的幅宽、长度以及矩形样片的相关尺寸参数如表1所示。

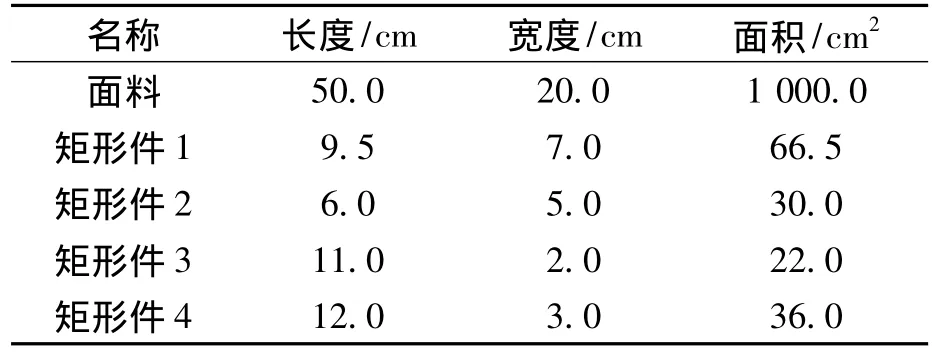
表1 面料和4种矩形样片的尺寸表

由于每种矩形样片都有两种排列方式，因此n种矩形样片的排料方式共有2n种。当n=4时矩形样片的排料方式共有24=16种，即(γ1，γ2，γ3，γ4)为(1，1，1，1)、(1，1，1，0)、(1，1，0，1)、(1，1，0，0)、(1，0，1，1)、(1，0，1，0)、(1，0，0，1)、(1，0，0，0)、(0，1，1，1)、(0，1，1，0)、(0，1，0，1)、(0，1，0，0)、(0，0，1，1)、(0，0，1，0)、(0，0，0，1)、(0，0，0，0)。下面分别对这16种情况进行分类建模讨论。

对于第 1 种方式(γ1，γ2，γ3，γ4)=(1，1，1，1)，即4种矩形都竖排，则有:

c=min{［γ1a1+(1 － γ1)b1］，［γ2a2+(1 －γ2)b2］，［γ3a3+(1 － γ3)b3］，［γ4a4+(1 － γ4)·b4］}=min(a1，a2，a3，a4)=6

f=min{［(1 － γ1)a1+ γ1b1］，［(1 － γ2)a2+γ2b2］，［(1 － γ3)a3+ γ3b3］，［(1 －γ4)a4+γ4b4］}=min(b1，b2，b3，b4)=2

M=int(50/f)=15，X=int(20/c)=3，代入组合优化模型得:

该模型分解为以下几种情况:

(1)(x1j≠0)＆＆(x2j=0)＆＆(x3j=0)＆＆(x4j=0)，即全部是第1类矩形样片时优化模型为:

解得:x1j=2，m=7，面料利用率 η11=7×66．5 ×2/1 000=93．1%;

(2)(x1j=0)＆＆(x2j≠0)＆＆(x3j=0)＆＆(x4j=0)，即全部是第2类矩形样片时，同理可得:x2j=3，m=10，面料利用率 η12=3×30×10/1 000=90．0%;

(3)(x1j=0)＆＆(x2j=0)＆＆(x3j≠0)＆＆(x4j=0)，即全部是第3类矩形样片时，同理可得:x3j=1，m=25，面料利用率 η13=1×22×25/1 000=55．0%;

(4)(x1j=0)＆＆(x2j=0)＆＆(x3j=0)＆＆(x4j≠0)，即全部是第4类矩形样片时，同理可得:x4j=1，m=16，面料利用率 η14=1×36×16/1 000=57．6%;

(5)(x1j≠0)‖(x2j≠0)‖(x3j≠0)‖(x4j≠0)，即4种矩形样片不全部为0时，由于0≤xij≤3∩xij∈Z，而3种矩形样片单独排放时，在使面料利用率最高的情况下 x1j=2，x2j=3，x3j=1，x4j=1，故优化模型转化为:

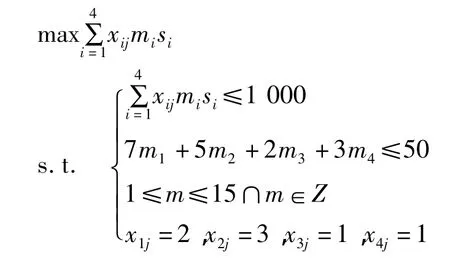
当上式取等号时，求解出(m1，m2，m3，m4)可能的取值。当 m1=5，m2=2，m3=1，m4=1 时，总面积=2×5×s1+3×2×s2+1×1×s3+1×1×s4=903。综上可知第 1 种方式(γ1，γ2，γ3，γ4)=(1，1，1，1)时，当 x1j=2，x2j=3，x3j=1，x4j=1，m1=5，m2=2，m3=1，m4=1 时，面料利用率最高为 η1=90．3%。

同理对于其他12种排料方式，可以分别得到面料利用率最高时，各参数的值，如表2所示。

对于(γ1，γ2，γ3，γ4)为(0，1，0，0)，(0，0，1，0)，(0，0，0，0)的这 3 种情况，没有满足条件的解。综上所述，可知当(γ1，γ2，γ3，γ4)=(1，0，0，1)，x1j=2，x2j=4，x3j=10，x4j=1，(m1，m2，m3，m4)=(1，3，2，1)时，能使面料的利用率最大为 η =96．9%。由此可以得到4种矩形的排料图如图1所示。

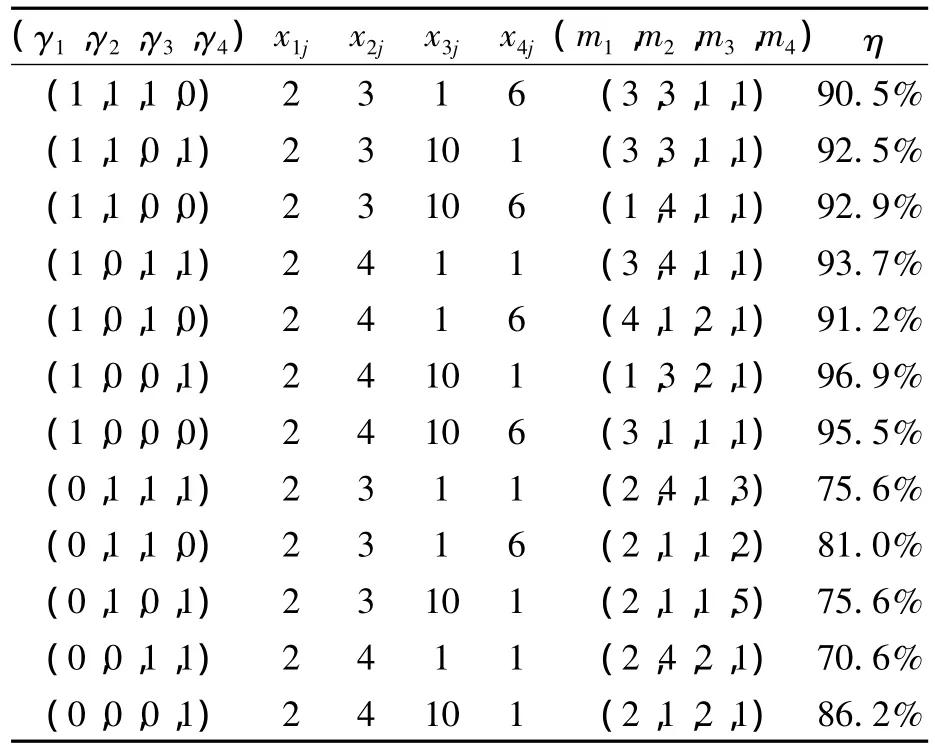
表2 剩余12种排料方式，面料利用率最高时各参数的数值表

图1 4种矩形的排料图

5 结论

笔者建立了混合组合方式下的服装排料数学模型并设计了组合优化算法，通过优化算法得到了矩形样片的最佳排料方案。最后，利用4种类型的矩形样片的排料问题验证了该模型的有效性。该服装排料的数学模型和组合优化算法能缩短排料时间，有效地提高面料的利用率，降低生产成本，为提高服装企业信息化水平发挥一定的作用。

［1］ 康立山，谢云，尤矢勇．非数值并行算法:模拟退火算法［M］．北京:科学出版社，2005:20－39．

［2］ 卢开澄．组合数学算法与分析［M］．北京:清华大学出版社，1983:41 －98．

［3］ PAPADIMITRIOU C H，STEGLITZ K．组合优化算法和复杂性［M］．刘振宏，蔡茂诚，译．北京:清华大学出版社，1988:50 －121．

［4］ ALBANO O．A heuristic solution of the rectangular cutting stock problem［J］．Operation Research，1977，25(l):70－81．

［5］ ADAMOWICZ A．A two stage solution of the cuttingstock problem［J］．Information Processing，1972(17):1086－1091．

［6］ HAIMS F．A multistage solution of the template layout problem［J］．IEEE Trans on Sys Sc．＆ Xyber，1970(2):302－310．

［7］ GILMORE P C，GOMORY R E．Multistage cutting stock problem of two and more dimensions［J］．Operation Research，1965，25(1):96 －120．

［8］ 周泓一，金廷赞．二维不规则形状的最优布局问题:计算机辅助服装裁片自动排料系统［J］．浙江大学学报:工学版，1988(3):92－99．

［9］ 徐彦欣，彭文．二维矩形板材排料的产生式规则方法［J］．机械设计，1997(6):35－37．

［10］ 刘德全，滕弘飞．矩形件排样问题的遗传算法求解［J］．小型微型计算机系统，1998(12):20 －25．

［11］ 赵宗金，陈秋娜．计算机优化排料［J］．电子工业技术，1996(4):166－172．

［12］ 李旭，严寒冰．服装CAD中衣片和排料模块技术的研究［J］．浙江工程学院学报，2000，17(3):166 －172．