光场-原子BEC相互作用系统的压缩特性

李 明，陈鼎汉

(桂林理工大学理学院 广西 桂林 541004)

玻色-爱因斯坦凝聚体(BEC)作为一种新的物质形态，从1995年在3种碱金属原子稀薄气体中实现以来，引起了研究热潮[1-3]。此后，人们对原子BEC的产生及其独特性质以及原子BEC与光场的相互作用进行了大量的实验和理论研究，取得了一系列成果[4-10]。通过光场和原子的相互作用可以实现光场的压缩，对于研究原子BEC与光场相互作用系统中光场的压缩性质具有重要意义。

本文在文献[11]的基础上，利用格子液体方法[12]对光场-原子BEC系统的总哈密顿量进行改进，并研究了二能级原子的玻色-爱因斯坦凝聚体与双模压缩光场相互作用系统中的压缩性质。

1 系统哈密顿量的改进和运动方程的求解

考虑原子间的相互作用，光场-原子BEC系统的总哈密顿量[11]为：

式中，0ω为原子基态和激发态之间的本征跃迁频率；b+和b分别为原子的产生算符和湮没算符；ω为光场的圆频率；ai+和ai(i=1,2)分别为第i模光场的产生算符和湮没算符；ε表征光场与原子相互作用的强度；Ω表征原子间相互作用的强度；Nc为玻色-爱因斯坦凝聚体的原子数。

2 双模光场的压缩效应

设初始时刻激发态为真空态，所有原子均处于基态并发生玻色-爱因斯坦凝聚。系统的初始态矢可表示为：

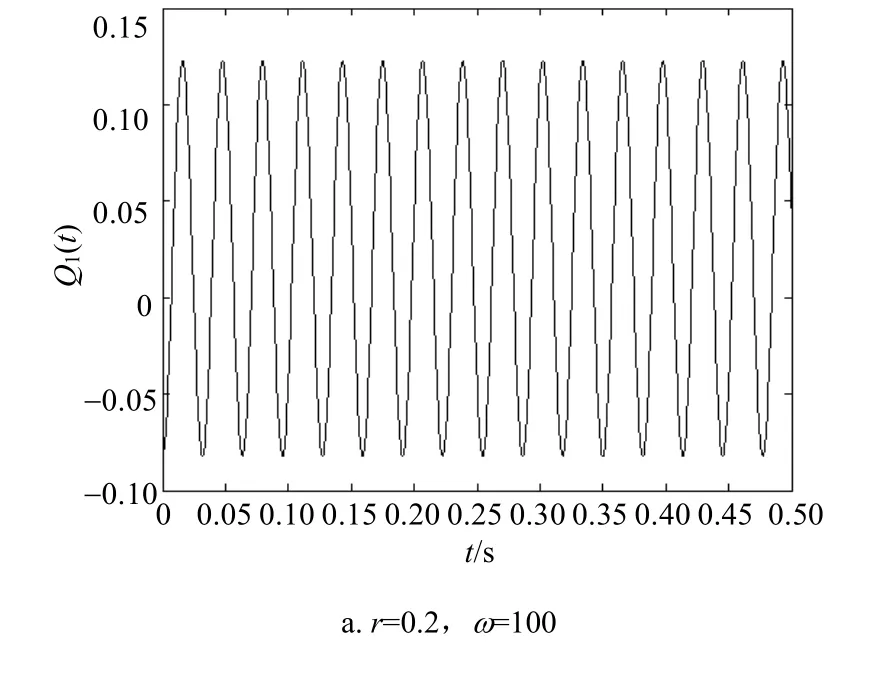
图1 在不同参数下Q1( t)随时间演化

在不同参数下Q1(t)随时间演化如图1所示。光场的两正交分量的涨落均随时间周期性地变化。对比图1a和图1b可知，当保持光场圆频率ω不变，而光场初始压缩因子r变化时，光场的最大压缩深度随r的增大而增大，而压缩时间不变。对比图1a和图1c可知，当保持光场初始压缩因子r不变，而光场圆频率ω变化时，光场的最大压缩深度不变，约为−0.08，而压缩时间随ω的增大而减少。

3 结 论

本文利用格子液体方法，对二能级原子的玻色-爱因斯坦凝聚体(BEC)与双模光场相互作用系统的哈密顿量进行了改进，并研究了二能级原子的玻色-爱因斯坦凝聚体与双模压缩光场相互作用系统中的压缩性质。结果表明，光场两正交分量的涨落均随时间周期性地变化，其压缩深度与光场初始压缩因子成正比，而压缩时间与光场的频率成反比。文献[11]只得出了影响压缩深度和压缩时间的主要因素，而本文则得出了它们之间的具体关系，与改进前的结果相比，改进后的结果与实际报道的结果更加符合(与文献[10]的结果一致)，对深入研究原子与光场相互作用过程中的压缩特性具有理论意义和实用价值。

[1] ANDERSON M H, ENSCHER J R, METHEWS M R, et al.Observation of Bose-Einstein condensation in a dilute atomic vapor[J]. Science, 1995, 269(5221): 198-201.

[2] DAVIS K B, MEWES M O, ANDREWS M R, et al.Bose-Einstein condensation in a gas of sodium atoms[J].Physical Review Letter, 1995, 75(22): 3969-3973.

[3] MEMES M O, ANDREWS M R, KURN D M, et al. Output coupler for Bose-Einstein condensed atoms[J]. Physical Review Letter, 1997, 78(4): 582-584.

[4] YOU L, LEWENSTEIN M, COOPER J. Quantum field theory of atoms interacting with photons[J]. Physical Review A, 1995, 51(6): 4712-4727.

[5] JING Hui, CHEN Jing-ling, GE Mo-lin. Quantumdynamical theory for squeezing the output of a Bose-Einstein condensate[J]. Physical Review A, 2001,63(1): 015601-015604.

[6] KUANG Le-man, ZHOU Lan. Generation of atom-photon entangled states in atomic Bose-Einstein condensate via electromagnetically induced transparency[J]. Physical Review A, 2003, 68(4): 043606-043614.

[7] ZHENG Gong-ping, LIANG Jiu-qing, LIU Wu-ming. Phase diagram of two-species Bose-Einstein condensates in an optical lattice[J]. Physical Review A, 2005, 71(5):053608-053612.

[8] XIE Zheng-wei, CAO Ze-xian, KATS E I, et al. Nonlinear dynamics of a dipolar Bose-Einstein condensates in an optical lattice[J]. Physical Review A, 2005, 71(2): 025601-025604.

[9] JI An-chun, LIU Wu-ming, SONG Jun-liang, et al.Dynamical creation of fractionalized vortices and vortex lattices[J]. Physical Review Letter, 2008, 101(1): 010402-010405.

[10] 周明, 黄春佳. 原子玻色-爱因斯坦凝聚体对光场压缩特性的影响[J]. 光学学报, 2009, 29(4): 1096-1100.ZHOU Ming, HUAUG Chun-jia. Influence of an atomic Bose-Einstein condensate on squeezing properties of light[J]. Acta Optica Sinica, 2009, 29(4): 1096-1100.

[11]] 赵丽云. 二能级原子双模光场系统中光场压缩性质[J].太原师范学院学报, 2009, 8(4): 74-77.ZHAO Li-yun. Squeezing properties of two-mode squeezed light field interacting with two-level atoms[J].Journal of Taiyuan Normal University, 2009, 8(4): 74-77.

[12] 胡英. 流体的分子动力学[M]. 北京:高等教育出版社,1982: 380-381.HU Ying. Molecular thermodynamics on fluids[M]. Beijing:High Education Press, 1982: 380-381.

[13] 李明, 孙久勋. 原子间相互作用对光场和原子激光压缩性质的影响[J]. 物理学报, 2006, 55(6): 2702-2707.LI Ming, SUN Jiu-xun. Influence of the interaction between atoms on the squeezing of light field and atomic lasers[J]. Acta Pysica Snica, 2006, 55(6): 2702-2707.

[14] 彭金生, 李高翔. 近代量子光学导论[M]. 北京: 科学出版社, 1996.PENG Jin-sheng, LI Gao-xiang. Introduction of modern quantum optics[M]. Beijing: Science Press, 1996.