Density Set Algorithm Search for Communities in Complex Networks

XIE Fu-ding, ZHANG Da-wei, HUANG Dan, ZHANG Yong, and SUN Yan

(1. College of Urban and Environmental Sciences, Liaoning Normal University Dalian Liaoning 116029;2. Department of Computer Science, Liaoning Normal University Dalian Liaoning 116081)

Density Set Algorithm Search for Communities in Complex Networks

XIE Fu-ding1, ZHANG Da-wei2, HUANG Dan2, ZHANG Yong2, and SUN Yan2

(1. College of Urban and Environmental Sciences, Liaoning Normal University Dalian Liaoning 116029;2. Department of Computer Science, Liaoning Normal University Dalian Liaoning 116081)

To detect communities in complex networks, a density set algorithm (DSA)is proposed by introducing the concept of density set. The key idea of the algorithm is to constantly construct density sets in a network and decide whether the density set founded later can lead to generate a new community or amalgamate it with an old one. Step by step, the networks with apparent community structure can be partitioned well by the proposed method. The running time of DSA is approximately O(n+m)for a general network and O(n)for a sparse network, where n is the number of nodes and m the number of edges in a network. Tests on three typical real world networks and a benchmark reveal that DSA produces desired results. So the proposal is reasonable, and has the potential for wide applications in physics and computer science.

complex network; community; density set

Networks are used as a foundation for the mathematical representation of a variety of complex systems in many fields. Among many others,prominent ones include biological and social networks,Internet, information networks[1-5], and metabolic networks. For a complex network, its community structure is an important topological characteristic. In real-world networks, it is common to have small sets of nodes highly connected with each other but with only a few connections with the rest of the nodes. It is crucial to find the clusters of a network in order to understand its internal structure.

The community structure of complex networks is a heavily studied problem in science community. A large number of methods have been developed to detect community structure in networks in the past years. There are mainly two kinds of clustering algorithms, one is partitioning algorithm, and the other is the hierarchical clustering method. Kernighan-Lin algorithm[6]and spectral bisection algorithm[7]are the classical representatives, respectively. They can find the community structure efficiently in the networks in the case that the number of communities in the networks is given before. Depending on whether they focus on the addition or removal of edges from the network, the hierarchical clustering algorithms can be classified in two groups: the agglomerative methods and divisive methods. They usually compute the intensity of link between each pair nodes based on different methods, such as edge betweenness[8-9], edge clustering coefficient[10], information centrality[11],clustering centrality[12], node similarity[13], and so on.Then, by repeatedly incorporating the two nodes with the highest intensity of link (agglomerative method), or repeatedly removing the edge with the lowest intensity(divisive methods), the partition results of the networks are obtained. To measure a specific division of a network into communities, Ref. [14]introduced the modularity Q. Bigger modularity corresponds to a better detection of community structures. Ref. [15]proposed a quantitative function (modularity density)for community partition, and declared that this quantitative function is superior to the widely used modularity Q. Ref. [16]proposed the concepts of accuracy and precision to evaluate the partition result of the network. A fast and efficient algorithm that searches for the communities in a network was depicted by Ref. [17]in 2009. The key strategy is mining a node with the closest relations with the community and assigning it to this community. The local modularity method was proposed by Ref. [18].The utilization of local modularity will generally give rise to the increase of the computation speed because local information in the network is only related. The more methods, techniques and development to extract the communities in networks were introduced by Ref. [19].

It is a common case that some nodes in a network can belong to more than one community, which means an overlapping community structure in complex networks. In this framework, each node has a certain probability of belonging to a certain cluster, instead of assigning nodes to specific clusters, which is called fuzzy clustering or fuzzy partition in some papers[20-23].For the nodes lying in the transition domain between different clusters, the fuzzy partition will be more acceptable, which is given more reasonable explanations in some cases.

To describe the definition of community quantitatively, Ref. [10]proposed the strong and weak definitions. In a strong community, each node has more connections within the community than with the rest of the network, and in a weak community the sum of all degrees within the community is larger than the sum of all degrees toward the rest of the network. By comparing the above definitions, Ref. [24]proposed a comparative definition for community in networks. A community is defined as a set of nodes, which satisfies the requirement that each node degree inside the community should not be smaller than the node degree toward any other communities. This definition is in the middle of the strong and weak definitions. Hu’s definition quantitatively tells us how to tie a node to a known set.

In this paper, an algorithm is proposed to partition a network into clusters. The node with a maximal degree in a network is found and a density set is constructed and labeled. For the rest of the nodes(except nodes in the known density set), we search for a new density set and determine whether this set leads to generate a new community or not. Step by step, all nodes in a network will be labeled. This algorithm only relates to local information, so its running time is significantly reduced. The computational complexity of the proposed method is approximately O(m+n)for a general network, and O(n)for a sparse network, where n is the number of vertices and m is the number of edges in the network. The algorithm is tested on a benchmark and three real-world networks which are widely used in complex networks, and desired results are obtained. This implies that the proposed algorithm can provide a proper partition.

1 Density set algorithm (DSA)

Let G=(V,E)be an undirected and unweighted network or graph consisting of the set of nodes V(|V|=n), the set of edges E(|E|=m), and a symmetric adjacency matrix A, whose elements Aijare equal to 1 if i points to j and 0 otherwise. In what follows, we would like to use simply i instead of vifor indicating nodes. The degree of node i is denoted as di, and Ai=(Ask)is its neighbor matrix, where node s and node k are the neighbors of node i.

Up to now, no definition of community has universally been accepted. Generally, a community is defined as a set of nodes, which satisfies the requirement that each node degree inside the community should not be smaller than the node degree toward any other communities. It is known that different networks carry different connection densities.Even within the same network, different clusters also show different connection densities. To describe the compactness of community quantitatively, Ref. [10]introduced the following strong community definition.

Definition of community in a strong sense: the subnetwork C is a community in a strong sense if for any node i belongs to C, we have

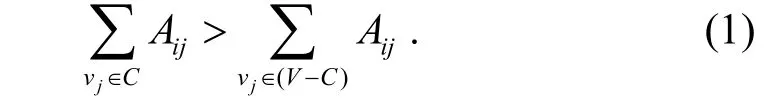
Obviously, not all communities in networks are strong. However, it is interesting to investigate the subset S of V which satisfies Eq. (1)but consists of a part of a community we want to extract from a network.This is because that the nodes in S are always in the same community no matter which algorithm is applied.That is to say, the structure of set S is stable in the procedure of partitioning networks into groups. We call such set S ‘density set’ or ‘strong structure’.

Now, the question is how to search for density sets in a given network and detect communities by using these sets. From the sociology point of view and enlightening from the example of Karate club, we know that the node with a high degree has more powerful agglomeration than the one with a low degree in a network. This implies that it is possible to construct a density set by considering the former and its neighbors.

In what follows, we present the description of DSA in detail.

Let V1=V−D1. Repeating the above process, one can get the density set D2in V1. It is necessary to decide whether set D2leads to a new community or it is amalgamated with D1.

To be conveniently, the following notations are introduced in order to depict the conditions clearly.

If Disatisfies one of the following three rules, we can conclud that it will give rise to a new community,and label all the nodes in this set.

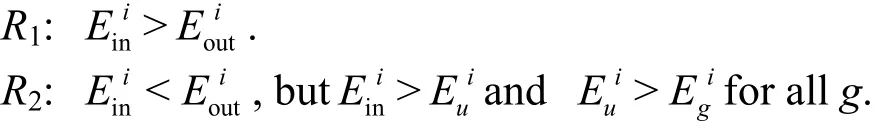
R3: Diconsists of at least three vertices and its neighbors are all in an unknown community.

It is obvious that a new density set will not always satisfy above conditions. In this case, it needs to be amalgamated with one of the known communities under the conditions, i.e.,

In this case, we do not know how to further operate this density set. Therefore, the best idea is to label it as an undetermined set.

All communities will be founded after all the nodes in a network have been labeled and there is no undetermined density set. If existed, we execute the following procedure A:

Step 1: Search for the node j with a maximal degree in all undetermined sets.

Step 4: Repeat steps 1～3, until there is no undetermined set or node.

When this procedure is over, it is obvious that all communities in the network have been obtained. The whole algorithm is described as follows.

Input: A complex network G = (V, E).

Output: Community structure of network.

Step Ⅰ: Search for the node i with a maximal degree and its neighbors in set V. Compute bsand αs,and construct density set Di. Label the nodes in Diaccording to rules R1, R2,, R5.

Step Ⅱ: Let V=V−Di, while V≠ null, go to step 1.

Step Ⅲ: If there exists an undetermined set call Procedure A

else output communities.

The main time consumption of the proposed algorithm is in the process of constructing the density set, which involves the following two steps. The first is to find the neighbors of node i. It is easy to obtain them in O(di), where diis the degree of node i. The second is to construct the density set Diand decide whether or not this density set leads to a new community. The required time for this step is at most O(di+3mi), where miis the number of edges in Di. The running time of extracting the density set Diis about O(2di+3mi), or simply O(di+mi). Therefore, the running time of stepⅠ in the algorithm is approximately O(n + m). In general, the running time of procedure A does not overrun O(n+m). The complexity of the proposed method is linear because the algorithm always employs the local information about a given vertex and its neighbors, but not the global information about the whole network.

2 Application of DSA

In this section, to confirm the performance of the proposed algorithm, three classical real-world networks with a known community structure and a benchmark are chosen. Java language and Eclipse RCP IDE are used to implement the algorithm on PC with 2.66 GHz duo processor and 2 GB memory.

2.1 College football network

The first example is the network of the schedule of Division I games for the world of US college football 2000 season[22]. In this network, vertices represent teams and edges represent regular season games between the two teams they connect. One has already known in advance that there are 12 communities in this network and each community contains around 8 to 12 teams. The characteristic this network carries is that the degrees of its nodes vary from 7 to 12 and the average degree is about 10.6. That is, there is no apparent center node like nodes 1, 33 or 34 in Zachary’s karate club network[25].

For this network, steps Ⅰ and Ⅱ in the proposed algorithm are executed 44 times and initially 25 density sets are obtained. Then the Procedure A is called 20 times and as a result, 11 communities are detected with 5 communities coinciding with the real groups. Total of 91.3% of teams are put in correct communities. The whole correct result is not obtained because some teams play with the teams in their own community nearly as much as with the teams in other communities. The algorithm can not find the teams like node 110 which has more connections with other communities than with the vertices in its own community. The partition result can be seen in Fig.1 and comparison results are listed in Tab.1.

Table 1 Comparison of the result of our algorithm OM with other well-known algorithms which are, in order, GN[9],FCM[22] and LP[26].

2.2 Les Misérables network

Les Misérables network complied by Ref.[27]reflects the interactions between major characters in the novel Les Misérables written by Victor Hugo. For this network, the vertices represent characters and an edge between two vertices represents simultaneous appearance of both characters in one or more scenes.Fig.2 shows the community structures detected by the proposed method. Four communities reflect clearly the subplot structure of the book: Jean Valjean (node 11)and the police officer Javert (node 27)are center of the largest communities representing the protagonists in the novel. Marius (node 55)and Gavroche (node 48)are the key characters in another community. Fantine(node 23)and bishop Myriel (node 0)lead the rest two communities respectively.

Fig. 1 The community structure of USA College Football network detected by the proposed algorithm

Fig.2 Community structure for the Les Misérables network

2.3 Books on American politics network

The final example is V.Krebs’ network of books on American politics introduced by Ref. [28]. In this network the vertices represented 105 recent books on American politics bought from the on-line bookseller Amazon.com, and edges join pairs of books that are frequently purchased by the same buyer. Ref. [28]divided the books into 3 types: liberal, conservative or centrist with no clear affiliation. Fig. 3 shows the result achieved by the proposed algorithm. The community in the left represents the liberal books, the right one represents almost entirely the conservative books, and the middle group denotes the centrist. In the result, left group includes 3 centrist books and 2 right wing books besides liberal books. The right one has more centrist books than the left but no liberal books. The middle one consists of 4 centrist books, 5 liberal books and 2 conservative books. These books in different communities are almost identical with the actual division according to political orientations. Rectangles represent books and edges join books frequently purchased by the same readers.

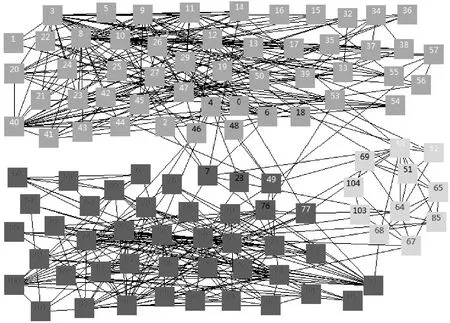
Fig.3 The partitioning of the American Political Books network found by the proposed algorithm.

3 The comparison of the results

In this section, we have used a benchmark to test the performance of our algorithm and the other three famous algorithms to detect communities in networks,i.e., extremal optimization algorithm[29], GN fast algorithm[14], spectral optimization algorithm[29]. The benchmark introduced by Ref. [30]is an artificial network of which both the degree and the community size distributions are power laws, with exponents α(α=2,3)and β(β=1,2), respectively. The parameters we take in this benchmark are α=2, β=2, number of nodes=500, average degree=15, max degree=50,minimum for the community sizes=20 and maximum for the community sizes=50, respectively.

From Fig. 4, it is easy to see that our algorithm runs fastest in the four algorithms. This result confirms our analysis of time complexity. When pout≤0.4, it shows that the accuracy of division of this benchmark obtained by our algorithm is higher than those achieved by the other three algorithms in Fig. 5a This implies that the network with an apparent community structure can gain a good partition by the proposed algorithm. The curves in Fig.5b show that the number of communities found by the proposal is always close to the original one. Maybe, the result can be thought as an indicator when we deal with the clustering problems(for example C-means algorithm).

The curves correspond to time complexity of our algorithm and spectral optimization algorithm respectively in right side since they are too close to be distinguished in left side.

Fig. 4 The comparison of the time complexity of four algorithms and the scaling of the computer time (in ms)with Pout

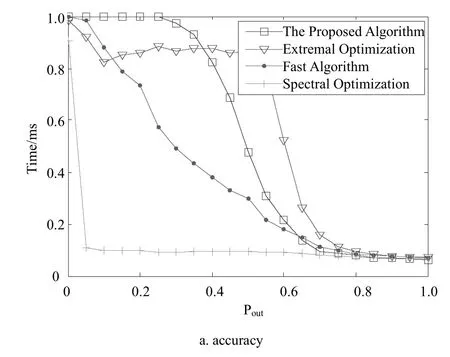
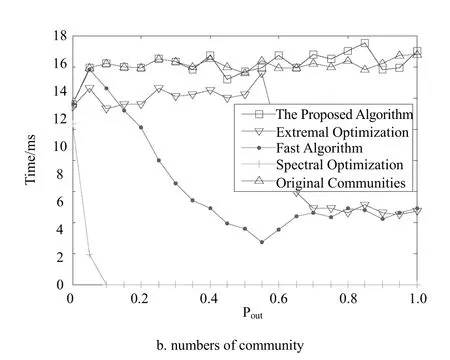
Fig. 5 The scaling of the accuracy of division of the benchmark computed by four algorithms with Pout, and the variety of the numbers of community detected by different algorithms in the benchmark with Pout.

4 Discussion and conclusion

Since the structure of the density set is stable in the procedure of partitioning a network into groups, it is possible to obtain the community structure of a network by searching for density sets in this network.Obviously, not all the density sets can lead to a new community. Thus, it is necessary to introduce some conditions to decide whether the density set constructed later can generate a new community. The process of constructing density sets only relates to local information, i.e., a node and its neighbors. Unlike the existed agglomeration algorithms, we tie all the batch nodes to a known set simultaneously. These imply that our algorithm can fast detect communities in a network.

In summary, we develop an algorithm to extract community structures from the networks. It runs in time O(m+n)for a general network, and O(n)for a sparse network, where n is the number of vertices and m the number of edges in the network. This is considerably faster than most previously reported algorithms, and allows the extend community structure analysis for the networks that were considered too large to be tractable in the past. The proposed algorithm is tested on a benchmark and three networks with known community structures, and the results indicate competitive performance. The method is expected not only to allow the extension of community structure analysis to some of the very large networks,but also prove useful in the analysis of many other types of networks.

[1]STROGATZ S H. Exploring complex networks[J]. Nature(London), 2001, 410: 268-276.

[2]ALBERT R, BARABASI A L. Statistical mechanics of complex networks[J]. Rev Modern Phys, 2002, 74: 47-97.

[3]STEINHAEUSER K, CHAWLA N V. Identifying and evaluating community structure in complex networks[J].Patt Recog Lett, 2010, 31: 413-421.

[4]MA X K, GAO L, YONG X R, et al. Semi-supervised clustering algorithm for community structure detection in complex networks[J]. Physica A, 2010, 389: 187-197.

[5]PUJOL J M, BEJAR J, DELGADO J. Clustering algorithms for determining community in large networks[J]. Phys Rev E, 2006, 74: 016107.

[6]KERNIGHAN B W, LIN S. An efficient heuristic procedure for partitioning graphs[J]. Bell Syst Tech J, 1970, 49:291-308.

[7]FIEDLER M. Algebraic connectivity of graphs[J]. Czech Math J, 1973, 23: 298-305.

[8]NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Phys Rev E, 2004, 69:026113.

[9]GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proc Natl Acad Sci, 2002,99: 7821-7826.

[10]RADICCHI F, CASTELLANO C, CECCONI F, et al.Defining and identifying communities in networks[J]. Proc Natl Acad Sci, 2004, 101: 2658-2663.

[11]FORTUNATO S, LATORA V, MARCHIORI M. A method to find community structures based on information centrality[J]. Phys Rev E, 2004, 70: 056104.

[12]YANG B, LIU J. Discovering global network communities based on local centralities[J]. ACM Trans on the Web, 2008,2(1): 1-32.

[13]PAN Y, LI D H, LIU J G, et al. Detecting community structure in complex networks via node similarity[J].Physica A, 2010, 389: 2849-2857.

[14]NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Phys Rev E, 2004, 69: 066133.

[15]LI Z P, ZHANG S H, WANG R S, et al. Quantitative function for community detection[J]. Phys Rev E, 2008, 77:036109.

[16]FAN Y, LI M H, ZHANG P, et al. Accuracy and precision of methods for community identification in weighted networks[J]. Physica A, 2007, 377: 363-372.

[17]CHEN D B, FU Y, SHANG M S. A fast and efficient heuristic algorithm for detecting community structures in complex networks[J]. Physica A, 2009, 388:2741-2749.

[18]CLAUSET A, NEWMAN M E J, MOORE C. Finding community structure in very large networks[J]. Phys Rev E,2004, 70: 066111.

[19]FORTUNATO S. Community detection in graphs[J]. Phys Rept, 2010, 486: 75-174.

[20]PALLA G, DERENYI I, FARKAS I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435: 814-818.

[21]REICHARDT J, BORNHOLDT S. Detecting fuzzy community structures in complex networks with a Potts model[J]. Phys Rev Lett, 2004, 93: 218701.

[22]ZHANG S H, WANG R S, ZHANG X S. Identification of overlapping community structure in complex networks using fuzzy c-means clustering[J]. Physica A, 2007, 374:483-490.

[23]LIU J. Detecting the fuzzy clusters of complex networks[J].Pattern Recognition, 2010, 43: 1334-1345.

[24]HU Y Q, CHEN H B, ZHANG P, et al. Comparative definition of community and corresponding identifying algorithm[J]. Phys Rev E, 2008, 78: 026121.

[25]ZACHARY W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research, 1977, 33: 452-473.

[26]AGARWAL G, KEMPE D. Modularity-maximizing graph communities via mathematical programming[J]. Eur Phys J B, 2008, 66: 409-418.

[27]KNUTH D E. The stanford graphBase: a platform for combinatorial computing[M]. Addison-Wesley, Reading,MA, 1993.

[28]NEWMAN M E J. Modularity and community structure in networks[J]. Proc Nat Acad Sci, 2006, 103: 8577-8582.

[29]DUCH J, ARENAS A. Community detection in complex networks using extremal optimization[J]. Phys Rev E, 2005,72: 027104.

[30]LANCICHINETTI A, FORTUNATO S, RADICCHI F.Benchmark graphs for testing community detection algorithms[J]. Phys Rev E, 2008, 78: 046110.

编 辑 蒋 晓

2011- 06- 15

国家自然科学基金(10771092)

谢福鼎(1965- )，男，博士，教授，主要从事人工智能、数据挖掘及计算机代数方面的研究.

寻找复杂网络社团的稠密集算法

谢福鼎1，张大为2，黄 丹2，张 永2，孙 岩2

(1. 辽宁师范大学城市与环境科学学院 辽宁 大连 116029; 2. 辽宁师范大学计算机与信息技术学院 辽宁 大连 116081)

通过引入稠密集的概念，该文提出了一种基于稠密集的寻找复杂网络中社团结构的算法。算法的主要思想是在网络中不断构造稠密集，并判断后生成的稠密集能否导致产生一个新社团，还是将其与一个已有的社团合并。利用该算法可以将具有明显社团结构的网络进行比较合理的划分。在一般情况下，该算法的时间复杂度约为O(n+m)，对于稀疏网络的时间复杂度约为O(n)，其中n为网络的节点数，m为边数。对3个典型实际网络和一个标准测试网络的试验结果表明，该方法获得了理想的社团结构划分。该方法在计算机、物理及其他学科领域具有广泛的应用前景。

复杂网络; 社团结构; 稠密集

TP301.6

A

10.3969/j.issn.1001-0548.2011.04.001

date：2011- 06- 15

Supported by the National Natural Science Foundation of China under Grant(10771092)

Biography：XIE Fu-ding was born in 1965, and his research interests include artificial intelligence, data mining, computer algebra.

·物理电子学·