路况与地铁车辆振动关系的测试分析研究

张华超，张小栋，曹广忠

（1.西北工业大学动力与能源学院，陕西 西安 710072；2.深圳大学机电与控制工程学院，广东 深圳 518060）

0 引 言

车辆振动是评价车辆性能的一个重要指标，地铁车辆振动不但影响旅客乘车的舒适度，使驾驶员迅速疲劳，对车辆行驶安全性构成极大的威胁，而且能够引起轨道车辆某些部件的早期疲劳损坏，从而降低轨道车辆的使用寿命，在一定程度上制约了轨道交通的发展。影响车辆振动的因素很多，如车辆自身的减振性能、行车速度、行车线路状况等[1]。该文根据实际测量到的振动数据，对车辆振动与行车线路状况之间的关系做出分析。

1 理论分析

地铁车辆是一个多自由度的振动系统，作用于该系统的各种激扰力使其产生复杂的振动过程。引起车辆振动主要原因可以概括为：

（1）与轨道有关的激振因素，如轨道接头处的轮轨冲击、轨道的不平顺性等。

（2）与车辆结构有关的激振因素，如车轮偏心、车轮不均质等[2]。

另外，车辆动力设备和其他悬挂在车体上的辅助电气设备，如牵引电机、空调等产生的振动也会对车辆振动产生很大的影响。车辆振动模型如图1所示。

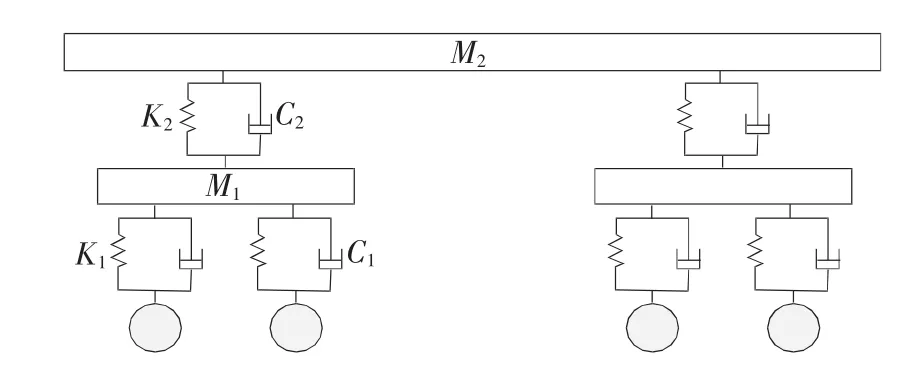
图1 地铁车辆振动模型

其中：K1、K2——一系和二系弹簧的刚度；

C1、C2——轮对与转向架和转向架与车体之间的阻尼系数；

M1、M2——转向架和车体的质量。

振动加速度有效值作为振动强度指标，表征了各个测点上振动的大小。其定义为

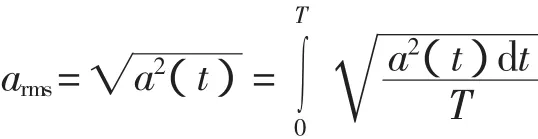
式中：arms——加速度有效值，m·s-2；

a（t）——加速度时程，m·s-2；

T——加速度持续时间，s。

可以通过检测车辆在运行过程中的振动加速度来评估车辆振动情况[3]。

2 测点选择

轨道不平顺是车辆振动的主要来源之一。轨道不平顺引起的随机激励导致转向架的振动，并通过转向架传递到车体，引起车体振动是地铁车辆振动产生的主要原因。

根据机车车辆随机振动分析的有限单元法研究[4]，车体振动加速度分布在两转向架和车体中心处幅值最大，所以选取1位端转向架部位地板a1点和车厢中央地板a2点2个垂向振动最明显的部位（如图2所示），采集这2个部位在不同路况下运行时的垂向振动信号，通过分析其垂向振动加速度有效值的变化，准确的判断不同路况条件下车辆振动加速度的变化情况，得出正确结论。

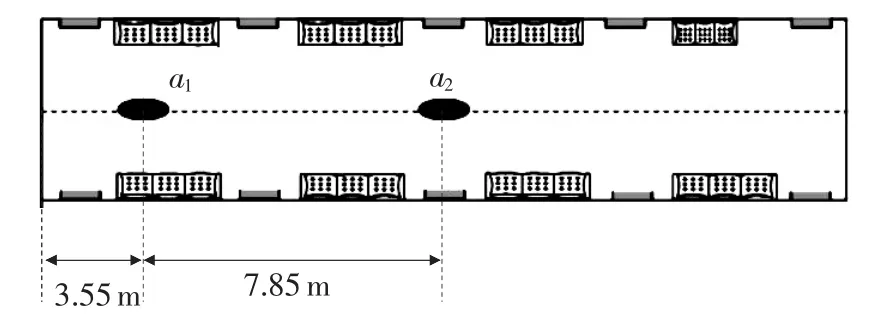
图2 测点分布

3 测试系统搭建

为完成该次测试，选用INV3018A型24位4通道智能信号采集分析仪和LC0156A型ICP振动加速度传感器以及1台PC机组建了振动测试系统，软件测试平台采用与信号采集仪配套的DASP-V10智能数据采集和信号处理软件。

4 测试方案

（1）测点分布，如图2所示。

（2）测试工况。以深圳地铁某线作为实验运行线路，以轨道的不平顺性作为激励输入，采集地铁车辆在60km/h匀速状态下全程运行的振动信号。

测试过程中，保证除路况以外其他引起振动的干扰因素保持最低水平，车辆在整个运行过程中空载，不必要的辅助设备（如广播等）关闭。

5 测试结果分析

作为参照，需要采集车辆在平直路段上以60 km/h匀速运行的振动信号。测试采集了地铁车辆在试车线上平直路段运行的振动数据作为参照。地铁车辆在试车线上的振动信号如图3所示。

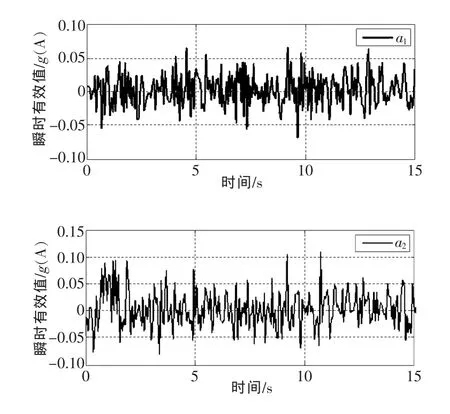
图3 试车线平直线路运行的时域图

数据采集过程中取3种不同路况：（1）坡度为3‰的下坡处，转弯半径为400m、长度为350m的弯道；（2）无弯道，坡度为10‰的下坡路段；（3）无弯道，坡度为10‰的上坡路段。采集这3种路况下60 km/h匀速运行的振动信号，并将这3种情况下采集的振动信与在试车线上采集的信号进行分析比较。

5.1 幅值域分析

3种路况下采集到的60 km/h匀速运行的时域信号图如图4所示。

试车线和3种其他路况下运行的总有效值统计比较如表1所示。

由有效值统计列表和振动信号时域图可以看出，在上、下坡路况条件下运行的地铁车辆的振动量级相对于平直的试车线有明显的增加，同时有坡度和弯道情况下的振动量级更大。这说明车辆运行线路状况对车辆振动量级影响显著。

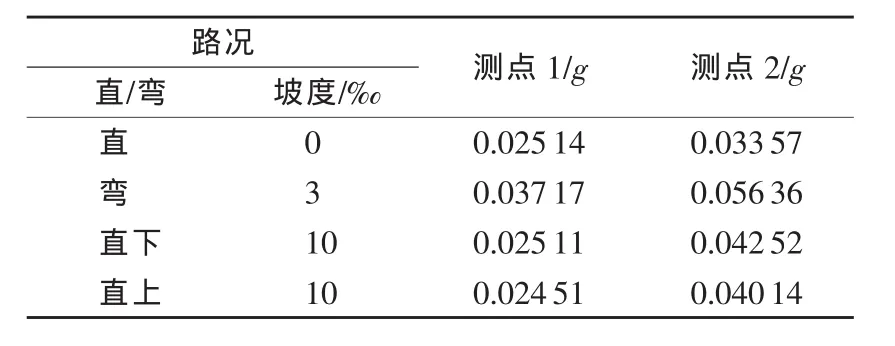
表1 不同路况下有效值统计

5.2 频域分析

将试车线及3种其他路况条件下采集的振动信号做FFT自谱分析，得到各种状态运行下车辆振动频率的能量分布。

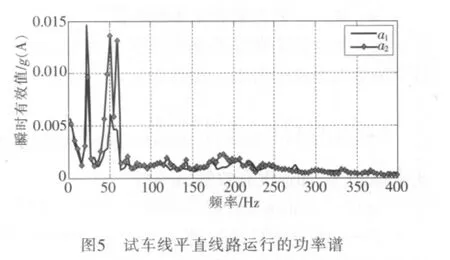
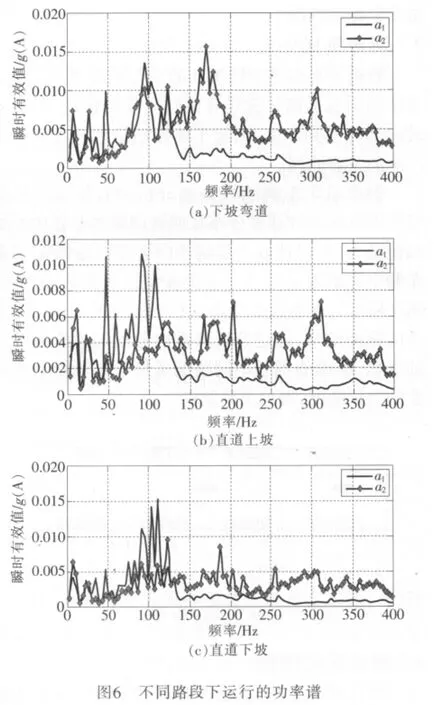
试车线上运行时振动的自功率谱如图5所示。其他3种路况下车辆振动信号的自功率谱如图6所示。

取测点1上的数据，做4种线路状态下振动信号的倍频程分析比较如图7所示。

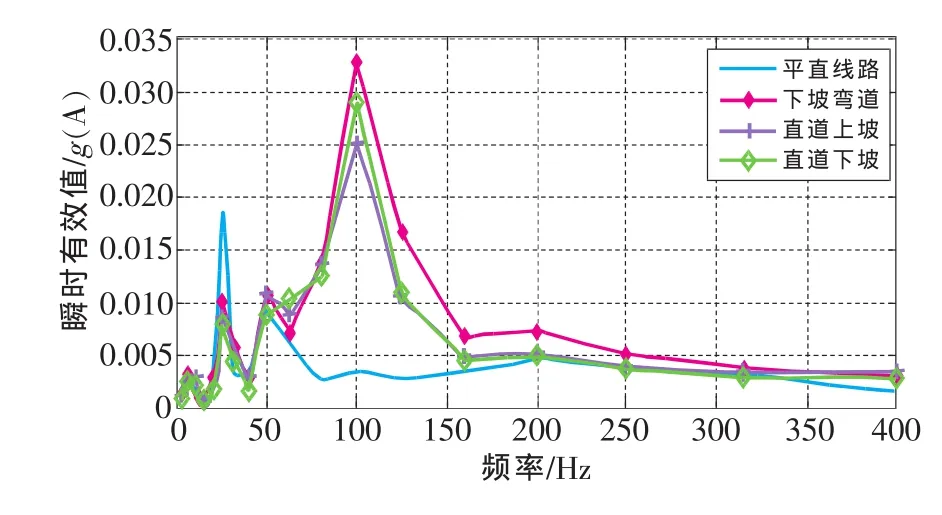
图7 1号测点4种路况的倍频程分析对比

由功率谱可以看出，在平直路段上，车辆振动能量主要分布在0～50Hz内。在非平直路段上行驶过程中，能量分布向较高频转移，主要集中在50～200Hz。由于车厢中部悬挂有空压机、制动电阻等电气设备，使得车厢中央部分在弯道运行过程时产生大量包含复杂频率的振动信号，且包含能量较大[5]。

由图7可以看出，非平直路段运行的地铁车辆，其在100Hz频率上振动量级最大。不同路况下100 Hz频率上的振动量级大小顺序如图7所示为：

下坡弯道>直道下坡>直道上坡>平直路段

6 结束语

该次测试中，共对4列不同的地铁车辆各3个车厢进行了相同条件下的实验，车辆振动信号表现出以下规律：

（1）车辆在非平直线路上行驶时，振动增大明显，其中弯道行驶过程中振动增大最明显。这是因为轮对与钢轨的接触面之间存在切向力，在一定条件下，这种切向力的激励作用越明显，使得车辆的振动加速度越大，这种振动属于车辆的自激振动[6-7]。

（2）车辆在上下坡运行过程中，振动量级也有较大幅度增加，坡度越大振动加速度越大；下坡产生时振动大于上坡产生的振动，这是因为在下坡过程中，要保持匀速必须对车辆由一个制动力以抵消重力分量。深圳市地铁车辆采用动力制动方式，制动时将牵引电机变为发电机，发电机产生电能由制动电阻以热的形式散发掉，这一过程中需要使用电扇对其进行强制散热，从而引起车体特别是车厢中央部位的振动增大[8]。

（3）地铁车辆在非平直线路运行时，振动能量主要集中在50～200 Hz，其中转向架上100 Hz左右包含能量最大，车厢中部由于结构和辅助设备影响频率成分复杂，能量分布较为分散[9]。

[1] 王伯铭.城市轨道交通车辆工程[M].成都：西南交通大学出版社，2007（9）：170-195.

[2] 陈泽深，王成国.铁道车辆动力学与控制[M].北京：中国铁道出版社，2004.

[3] 曾青中，韩增盛.城市轨道交通车辆[M].成都：西南交通大学出版社，2006.

[4] 向俊.机车车辆随机振动分析的有限单元法研究[J].长沙铁道学院学报，1995，13（4）：38-45.

[5] 贺启庸，倪纯双，王卫东.多体系统动力学与车辆动力学[J].铁道车辆，1995（1）：38-42.

[6]潘昌实，谢正光.地铁区间隧道列车振动测试与分析[J].土木程学报，1990，23（2）：21-28

[7] 王保坚.地铁车辆振动分析及解决方法[J].电力机车与城轨车辆，2009，32（3）：50-51.

[8] Stribersky A，Moster F，Rulka W.Structural dynamics and ridecomfort of a rail vehicle system[J].Advances in Engineering Software，2002（33）：541-552.

[9] Merovitch L.Elements of vibration analtisi[M].New York：Mcgraw-hall Book Company，1975.