OFDM移动通信系统中的最大多普勒估计
孟建刚,陈建春
(西安电子科技大学电子工程学院,陕西西安 710071)
多普勒频移是影响OFDM系统性能的重要参数之一,OFDM系统的多个环节如编码、调制、信道估计等都需要多普勒频移信息,因此多普勒频移估计将对整个OFDM系统的性能产生较大影响。目前大量的多普勒频移估计算法被提出[1-3]。文献[1]提出了一种基于循环前缀的自相关算法,该算法结构简单,但是在低速和低信噪比情况下,估计精度差。文献[2]提出了一种基于信道估计的自相关算法,在低速情况下有较好的估计精度,但是其估计精度主要取决于信道估计的精度。文献[3]中提出了一种基于最大似然函数的估计方法,其估计的精度很高,但实现的复杂度也大,难以应用于实际的系统当中。本文结合文献[1]与文献[2]中算法的特点提出了一种改良算法。通过在OFDM符号中插入已知的OVSF序列,利用OVSF序列的特点简便地求得信道的冲激响应,然后通过信道冲激响应的自相关,获得多普勒频移信息。仿真结果表明,本文提出的多普勒频移估计算法可以有效地估计出多普勒频移。
1 算法原理描述
Clarke[4]信道模型是用于描述小尺度衰落的一种平坦衰落信道模型,即瑞利衰落信道。其移动台接收信号强度的统计特性是基于散射的,这正好与市区环境中无直视通路的特点相吻合,因而广泛应用于市区环境的仿真中。因此,信道具有Jakes[5]功率谱模型
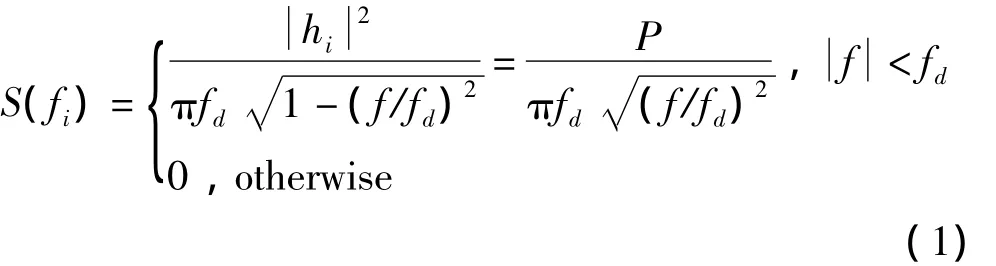
式中,hi是第i路的信道冲激响应;是信号的平均功率;fd是多普勒频移,它与速度v的公式为fd=fcv/c,这里fc为载波频率;c是光速,则信道冲激响应的归一化自相关函数由式(1)可得
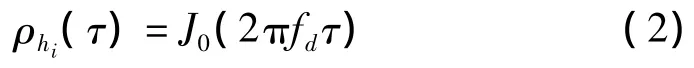
这里J0是第一类零阶Bessel函数,则
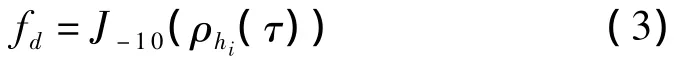
由此可知,通过信道冲激响应的自相关函数,运用式(3)就可得到最大多普勒频移。
2 系统模型
2.1 多普勒频移估计算法
假定接收信号r(t)为复基带信号,经过瑞利衰落信道,在加性高斯白噪声干扰下,其离散形式可以表示为
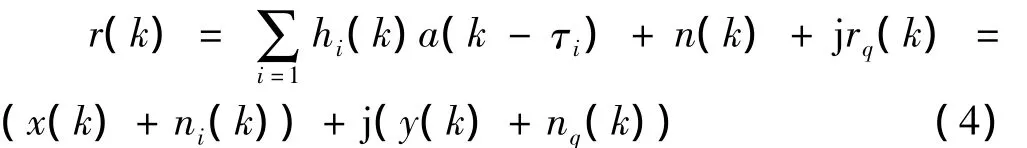
式中,a(k)为发送信号;x(k)和y(k)分别为a(k)经过信道以后期望信号的实部和虚部,且E[x2(k)]=E[y2(k)]=η2/2。n(k)=ni(k)+jnq(k)为复高斯加性白噪声且与信号不相关,其实部和虚部的功率为
接收信号的自相关函数为
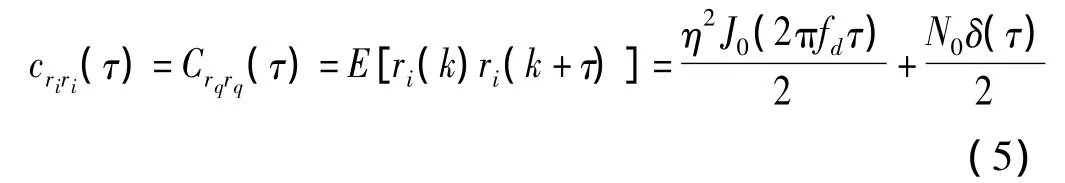
J0为第一类零阶Bessel函数。
如图1所示,在OFDM符号前面插入循环前缀,L为循环前缀长度,K为一个OFDM符号的子载波个数,T为采样时间,则一个包含循环前缀的OFDM符号的持续时间为Ts=(K+L)T。
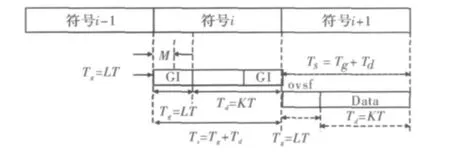
图1 OFDM符号结构
图2是该算法的结构图,ri(k)和rq(k)分别为接收信号的实部和虚部,ρi(KT,fd)和ρq(KT,fd)分别为实部和虚部所对应的自相关函数。
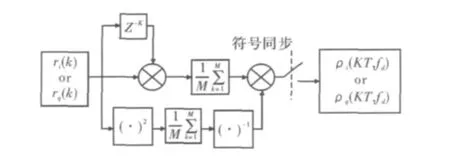
图2 算法结构图
本算法中不需要整个循环前缀GI都参加自相关运算,M的取值根据信道环境的不同而不同,在文献[1]中有关M取值的讨论,在此不作详细说明。利用式(5)可以求出最大多普勒频移fd。
2.2 改良的多普勒频移估计算法
如图1所示,在原有的循环前缀位置插入OVSF序列,OVSF序列的持续时间为Tg=LT,有效数据持续时间为Td=KT,T为采样时间,K为一个OFDM符号的子载波数目,L为插入的OVSF序列的长度,完整OFDM符号的持续时间为Ts=(K+L)T。
假设信号经过瑞利衰落信道,在理想的定时同步情况下,第i路径的接收信号可以表示为[6]
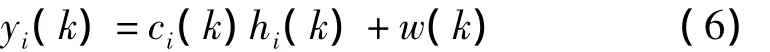
式中,ci(k)是 OVSF序列的元素;k∈[1,L],hi(k)是信道的冲激响应;w(k)是0均值,方差为σ2的复高斯白噪声,σ2取值在不同的路径下可能不同。
由于信号经过瑞利衰落信道多径传输,各个路径的能量可能不同,那么也就不同。为方便起见,这里假定hi就是由信号能量最强路径得到的信道冲激响应,根据文献[2],由式(6)可以得到hi为
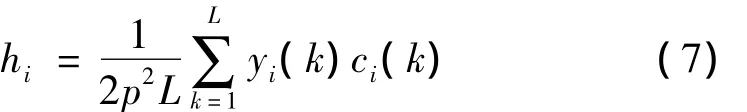
在文献[1]的算法原理基础上,进行信道冲激响应的自相关,该算法结构如图3所示。
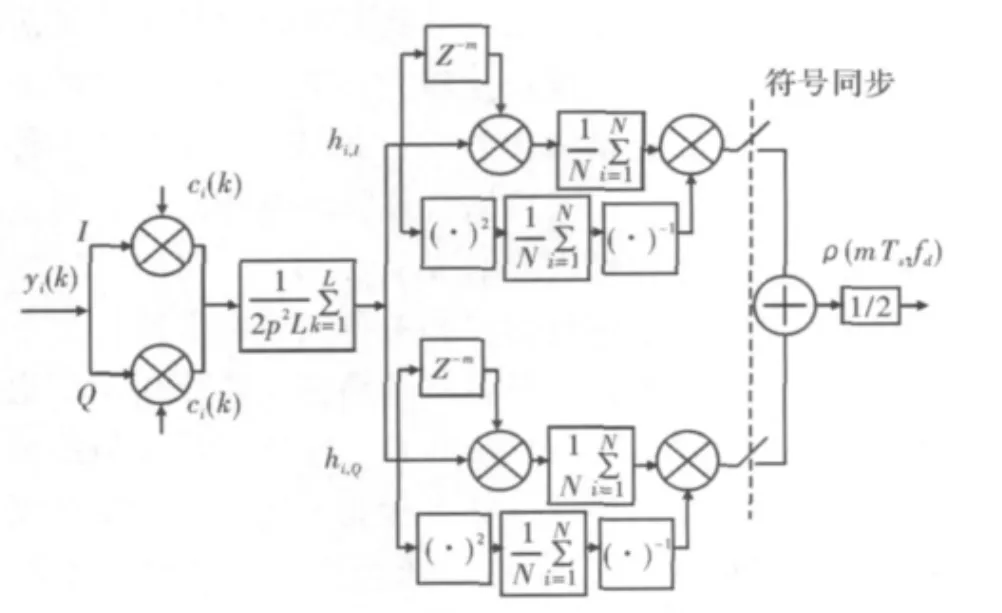
图3 多普勒频移估计算法结构图
hi,I,hi,Q是 hi的实部和虚部,N 是参加多普勒频移估计的符号数量,mTs是相关时间间隔,m是一个常数,它的取值将在下面讨论,则归一化的自相关函数可以表示为
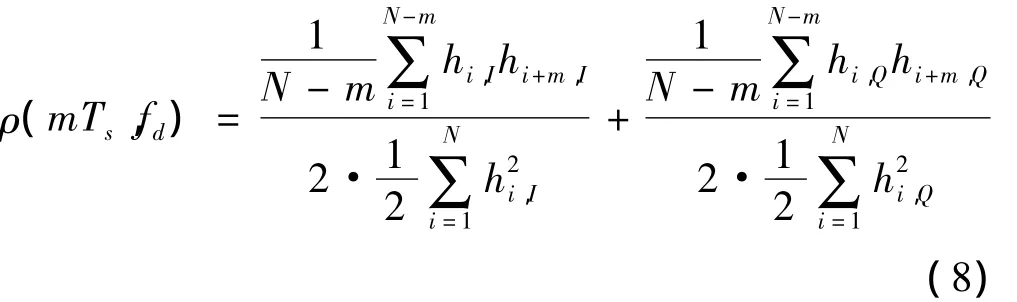
由此,通过式(3)和式(8)就可以求出最大多普勒频移fd。
3 仿真结果分析
在瑞利衰落信道下进行Matlab仿真,选取6路多径衰落,延迟的系数分别为 -0.2 μs,0 μs,0.6 μs,1.2 μs,和 5.5 μs,相 对 应 的 衰 落 系 数 分 别 为-3 dB,0 dB,-2 dB,-5 dB,-8 dB和-10 dB,选取数据长度K=3780,OVSF序列长度L=420,进行仿真的OFDM符号数量N=2000,常数P=6.5。符号率为 7.56 Mbit·s-1,那么 T=1/7.56 μs。调制方式为16QAM,载波频率fc=600 MHz。
算法中用到的第一类零阶Bessel函数是一个非线性函数,J0(x)的一个值可能对应着 x的多个值,因此必须把限定在第一个单调区间内,如图4所示,则
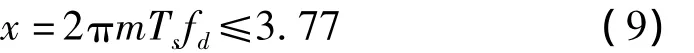
假定高速移动的火车速度达到350 km·h-1,那么多普勒频移fd=fcv/c将接近200 Hz,Ts=(L+K)T=555.6 μs,因此根据式(9),m取4最合适。J0(x)的取值可以由查表法求得。
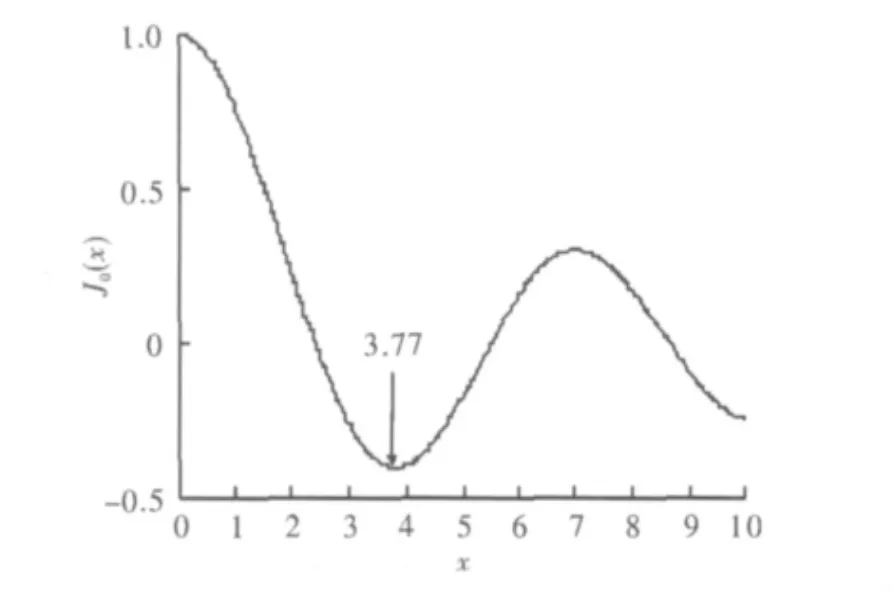
图4 第一类零阶Bessel函数
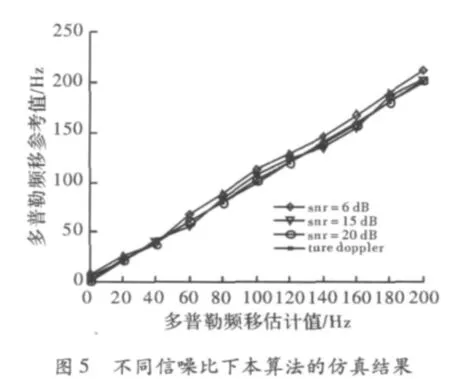
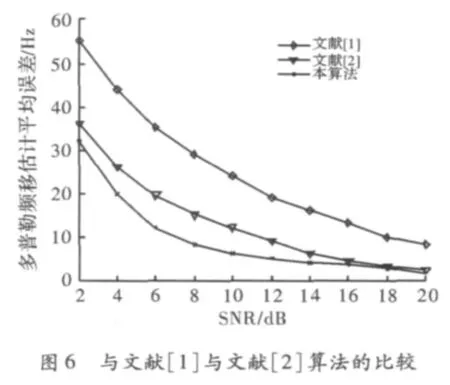
图5是不同信噪比下本算法的仿真结果,选取的多普勒频移范围在0~200 Hz之间,仿真结果表明,本算法在低速情况下有较高的精度,对信噪比的变化不是特别敏感,特别在40 Hz附近的精确度高于其他部分,在高速情况下也有良好的估计精度。图6是频率范围在0~200 Hz内,不同信噪比情况下多普勒频移的估计值与实际值平均误差对比,由图6可以看出,在不同信噪比下,本算法估计性能比文献[1]和文献[2]中算法的估计性能都好,特别在低信噪比情况下,与文献[1]算法相比,最高时平均误差将减少约20 Hz,与文献[2]相比,也有较大优势。
4 结束语
本文运用文献[1]中算法的原理,结合文献[2]中信道估计方法,提出了一种新的改良算法,本算法继承了两种方法的优点,发挥了OVSF序列的优势。仿真结果表明,在瑞利衰落信道下,本算法有着较高的估计精度,能够适应于较大范围内多普勒频移的估计,较文献[1]与文献[2]中的算法有着较大的优势,而且本算法复杂度较低,可以方便地运用到实际的OFDM系统中。
[1] CAI J P,SONG W T,LI Z.Doppler spread estimation for mobile OFDM systems in rayleigh fading channels[J].IEEE Trans on Consum Electron,2003,49(4):973 -977.
[2] LU Qiaoli,CHEN Wei,XIE Tao,et al.A doppler spread estimator design for mobile OFDM syestems[C].Singapore:2008 11th IEEE Singapore International Conference on Communication Systems,2008.
[3] CHOI Y S,OZDURAL O C,LIU H P,et al.A maximum likelihood doppler frequency estimator for OFDM systems[J].IEEE Trans on Consum Electron,2006(10):4572-4576.
[4] CLARKE R H.Principle of mobile communications[M].Boston:Luwer Academic Publishers,1996.
[5] JAKES W C.Microwave mobile communications[M].1sted.Piscataway:IEEE Press,1993.
[6] 韦岗,季飞,傅娟.通信系统建模与仿真[M].北京:电子工业出版社,2007.

