LTE上行信道估计技术研究
盛洪宁
(西安电子科技大学电子工程学院,陕西西安 710071)
LTE(Long Term Evolution)系统最大的改进在于采用了全新的空中接口技术,上行采用SC-FDMA多址接入技术,下行采用 OFDMA(Orthogonal Frequency Division Multiple Access)技术。SC-FDMA是结合OFDM可动态分配带宽的单载波多址接入方案,相对于OFDM技术,SC-FDMA系统的功率峰均比更低,有利于节省终端的成本和功率以及提高上行链路的覆盖范围[1-3]。
LTE上行的用户数据和控制信息主要是通过PUSCH(Physical Uplink Shared Channel)承载。PUSCH采用了块状参考信号结构,在一个子帧中插入2个导频符号。受到无线信道的时变特征、多径衰落和多普勒频移的影响,eNodeB接收到的往往是严重失真信号。因此,准确的信道估计是保证PUSCH传输质量、发挥其优越性的关键[4-6]。
本文将重点研究基于辅助导频的PUSCH信道估计技术,信道估计分为两个基本步骤:首先,估计出导频位置的信道响应;然后,根据导频位置的信道响应,运用插值算法恢复出全部数据位置的信道响应。衡量信道估计算法的优劣,主要考虑算法的复杂度和估计精度,目标是实现低复杂度的同时获得较好的估计性能。
1 LTE PUSCH传输方案
PUSCH采用了DFT-S-FDMA(Discrete Fourier Transform-Spread-FrequencyDivisionMultiple Access)技术。DFT-S-FDMA主要思想是数据在OFDM调制前,先进行DFT变换的预编码,实现了单载波的传输方案[7-8]。
如图1所示,在PUSCH基带调制过程中,输入的比特是经过信道编码的码字。首先,码字进行调制映射,生成复数符号 d=[d0,d1,…,dM]T,PUSCH支持多种调制方式,有 QPSK、16QAM和64QAM。然后,调制后复数符号进行M点DFT变换,得到 X(k),k=1,2,…,M。将 M点频域数据X(k)映射到相应的在载波资源上,并在一个子帧的第4和第11个符号插入导频序列。再进行N点IFFT变换,生成N点采样点x(k)。N与系统带宽有关,如系统为10 Mbit·s-1带宽时,N=1024。最后经过添加循环前缀、串并转换和数模转换,天线发射。
接收到的频域数据Y=[Y1,Y2,…,YNP],可以表示为
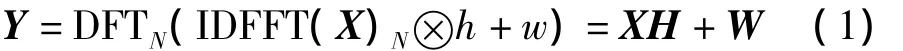
其中,h(k)是信道的离散响应,其频域响应为H;w(k)是加性噪声干扰,其频域响应为W;Np是导频长度,也是UE的子载波的个数;X=[X1,X2,…,XNP]是发射端频域数据和导频信号。信道估计的目的就是要获取信道的频域响应H。
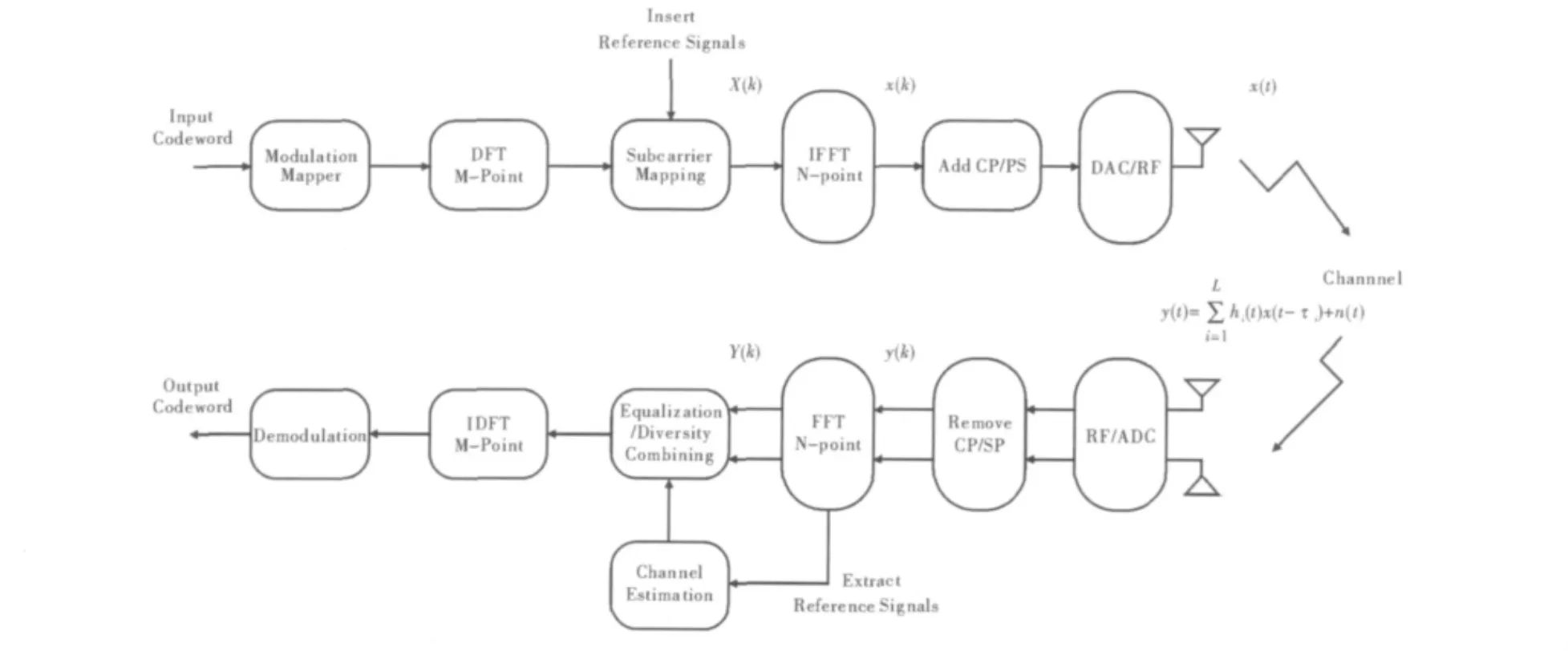
图1 PUSCH传输方案框图
PUSCH的导频结构如图2所示。黑色部分表示的是PUSCH导频信号的分布,频域上占据整个带宽,时域占用一个 Slot中 l=3的 SC-FDMA符号。PUSCH的参考信号分布是典型的块状导频结构,相对于其他的导频结构,块状导频结构特别适用于慢衰落信道的无线信道。在频域上导频覆盖了所有的子载波,因此频域上无需插值。
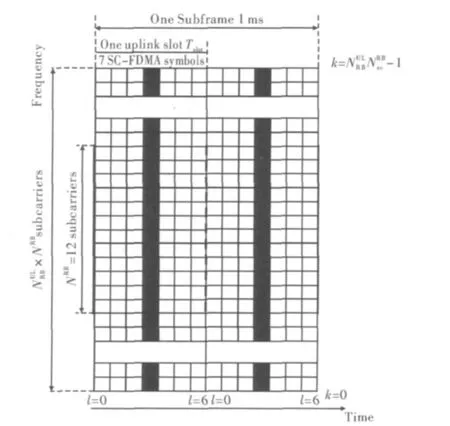
图2 LTE上行Subfarme的时频结构和参考信号(黑色部分)
实际上,接收端的过程要比发射端复杂得多,涉及到时间和频率同步、信道估计、均衡、分集合并和数据解映射等诸多关键技术。这里,假设在时频同步是理想情况下,进行信道估计研究。
2 信道估计
根据估计准则的不同,基于导频的信道估计方法常见有两种,最小二方差LS和最小均方误差MMSE算法。下面分别对这两种算法进行分析。
2.1 基于LS估计准则算法
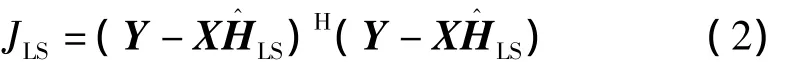
式中,Np表示参考信号的长度。根据代价函数最小准则,使JLS=0,得到
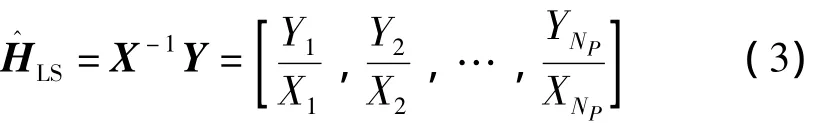
可见,频域LS信道估计方法算法简单,易于实现,因此得到广泛应用。但是,由于LS准则并没有考虑到噪声的影响,信道估计的结果将受到噪声的严重影响。如式(4)所示
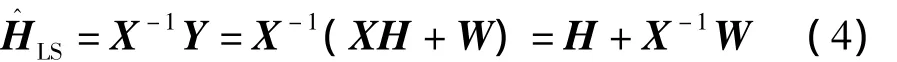
LS信道估计没有考虑噪声W的影响。因此,LS虽然算法复杂度低,实现简单,但是估计的误差较大,信道估计精度较低。
2.2 基于MMSE估计准则算法
为提高信道估计的精度,根据维纳滤波器理论[1],希望通过滤波器得到信道响应
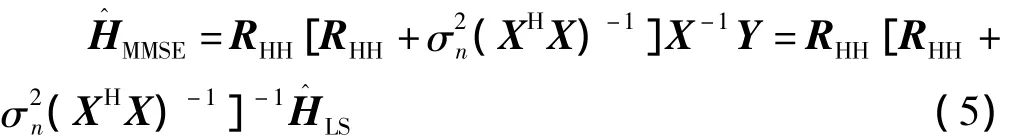

从式(5)可知,MMSE(Minimum Mean Square Error)估计方法实际上是对LS初估计结果进行一次滤波得到的信道估计。MMSE估计准则算法,是在最小均方误差意义上的最佳估计方法,精度较高。但是,这样的MMSE算法计算复杂度高,涉及到多次NP×NP复数矩阵的乘法和求逆,因此难以在实际系统中应用。
这里,对MMSES算法进行简化。首先,式(9)中的(XHX)-1,实际上导频信号可以确定,不需要实时计算导频信号的变化。根据3GPP TS36.211协议的定义,导频序列实际上是BPSK调制的信号,因此幅值这样,就有恒定(XHX)-1=1。由于功率控制的需要,(XHX)-1=,等于信号的发射功率,则有
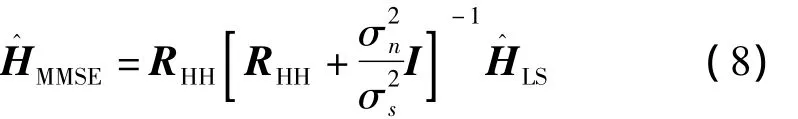
由信道的相关性特征可知,信道的自相关矩阵RHH=[rf(k1,k2)]由多径衰落的功率和时延决定,其时延功率谱服从负指数分布,一般相隔较远的子信道的相关小,与当前子信道邻近的自信道相关性较大。即频域上频率间隔较远的子载波相关性很小,频域上邻近的子载波相关性稍大。因此,可以对信道的自相关矩阵进行简化。
式(8)中,RHH=E[HHH]是一个NP×NP的矩阵
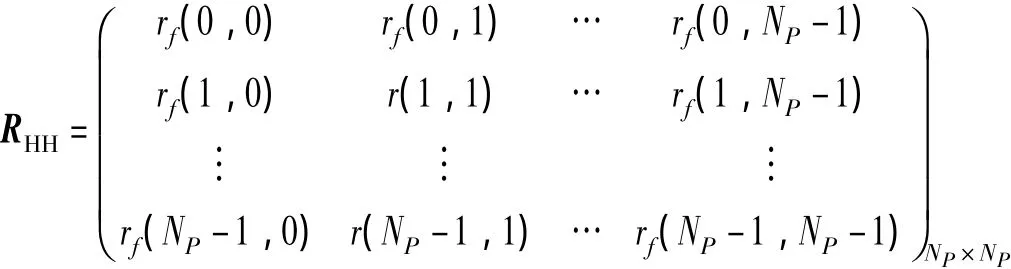

从R'HH矩阵可以看到,简化后的算法复杂度将大大降低。尤其当NP较大时,简化的运算量将是很大,原来一次矩阵乘法运算需要NP×NP次复数乘法运算,简化后只需要NP×L次,这样一次复数矩阵乘法运算就减少了NP×(NP-L)次乘法运算。
在实际应用中,经过简化的信道自相关矩阵RHH和噪声功率,可以通过实时测量获取,或者是根据真实信道的统计特性通过假设的方式预先确定,这样只需要一次乘法运算即可完成MMSE的计算。
在取得导频位置的信道估计值后,进而通过插值方法恢复出全部的数据位置的信道响应。常见的插值算法一阶线性内插性、二阶抛物线内插和基于DFT的插值方法等,不再赘述。
3 仿真结果及性能分析
本文仿真的LTE PUSCH参数配置如表1所示。这里对系统中的某个用户进行估计,该用户的上行资源为12个PRB。信道采用WSSUS信道模型,为广义平稳的多径时变瑞利衰落信道,6条多径的功率延迟谱服从负指数分布。

表1 系统仿真参数
信道估计算法性能的衡量指标是估计的均方误差MSE(Mean Square Error)和误符号率 SER(Symbol Error Rate),采用蒙特卡洛仿真方法,得到的仿真结果如图3和图4所示。
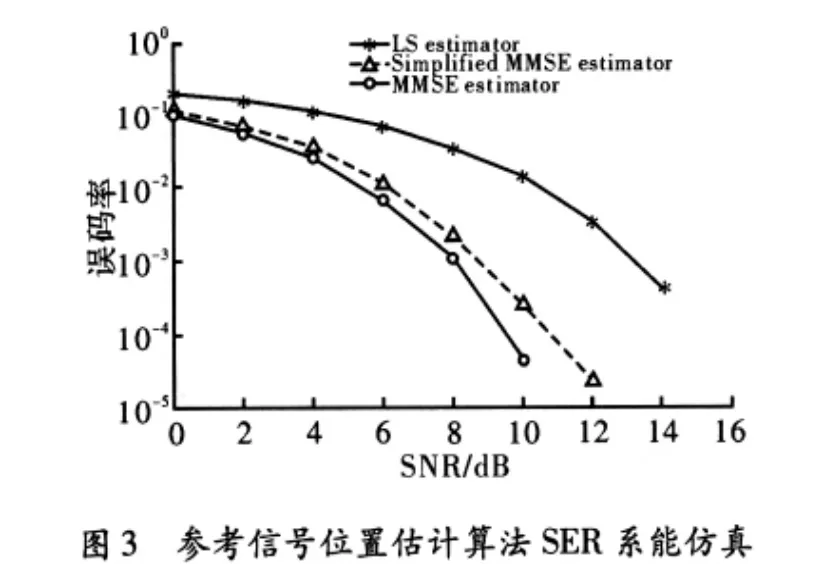
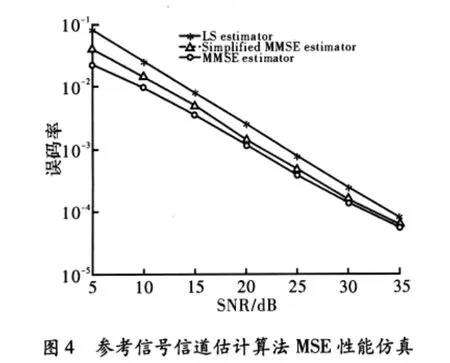
如图4所示,简化后的MMSE算法的误码率SER性能非常接近理想的MMSE算法性能,明显优于基于LS算法。例如在SNR=8 dB时,简化MMSE算法的误符号率比LS算法的SER约低10 dB,与MMSE算法相差约1 dB。同样,如图5所示,LS估计算法和MMSE估计算法在MSE性能上有较大的差距。显然,简化MMSE算法的估计精度接近MMSE算法,并明显优于基于LS准则的信道估计。
4 结束语
基于上述分析和仿真结果,简化算法用的整体性能优异,达到系统性能与复杂度的折衷。对于LTE PUSCH接收机信道估计,适于采用简化MMSE算法。该在实际应用中,信道的相关矩阵RHH和噪声功率可以通过实时地跟踪信道获取,也可以通过大量的真实信道的测量和仿真后设定为一个或一组固定值,这样较大程度地简化了运算过程,易于实现。
[1] SIMON HAYKIN.Adaptive filter theory[M].3rd Ed.New Jersey:Prentice Hall,Englewood Cliffs,1996.
[2] JAN -JAAP VAN DE BEEK,OVE EDFORS,MAGNUS SANDELL,et al.On channel estimation in OFDM system[C].Chicago:45th IEEE Vehicular Technology Conference,1995,2:815-819.
[3] 中兴通讯股份有限公司.3GPP TS 36.211 V870(2008-6),3GPP TSG RAN E-UTRA Physical Channels and Modulation(Release 8)[S].深圳:中兴通讯股份有限公司,2008.
[4] 中兴通讯股份有限公司.3GPP TS 36.212 V870(2008-6),3GPP TSG RAN E-UTRA Multiplex and Channel Coding(Release 8)[S].深圳:中兴通讯股份有限公司,2008.
[5] 曾召华.LTE基础原理与关键技术[M].西安:西安电子科技大学出版社,2010.
[6] 沈嘉,索士强,全海洋,等.3GPP长期演进(LTE)技术原理与系统设计[M].北京:人民邮电出版社,2009.
[7] 王军选.多径相关衰落下影响LTE系统容量因素分析[J].现代电子技术,2011(3):36-38.
[8] 许宁,蒋峰,徐凯.3GPP LTE小区间干扰协调方案研究[J].现代电子技术,2007(21):57-60,77.

