物元分析法在负荷密度指标求取中的应用

汤波，胡荣，符杨，宓佳璟，袁绍山

（1.上海电力学院电力与自动化工程学院，上海200090;2.上海市电力公司浦东供电公司，上海 201203）

负荷密度指标法是配电网规划中的重要方法，该方法通过对规划区内各地块的用地性质进行分析，确定相对应的负荷密度指标，进而对规划区负荷进行比较详尽的时空分布预测［1-3］.只有确定了供电区域内未来电力负荷增长的时空分布，才能对未来配电网新增电力设备的容量、投入时间、地点进行规划，特别是可以确定远期电力设备的建设规模，以便预留电力设施占地及保护线路走廊.

目前应用于负荷密度指标求取的方法主要有类比法、模糊理论等.类比法操作简单，但受预测者信息量及主观因素影响大;文献［3］运用模糊推理的方法对待预测区域土地开发和土地改造进行分析和研究，为其负荷密度指标的选取提供依据.文献［4］和文献［5］基于大量的调研数据，引入模糊贴近度理论和模糊综合评判方法求取负荷密度指标，量化了影响负荷密度指标的因素，使预测结果更加客观，但在样本分布属性密集时其预测精度有所降低，需采用聚类方法对样本进行处理，计算过程较为复杂.

本文提出了一种负荷预测的新方法，即采用物元分析法求取负荷密度指标.物元分析是我国著名学者蔡文于1984年创立的，是利用形式化工具从定量和定性角度来研究解决问题的规律和方法，已被广泛应用于模式识别、科学决策、方法拓展等领域［6-8］.笔者依据大量统计调研数据，将样本负荷密度指标、影响因素及其量值组成物元，建立负荷密度指标求取的物元模型，进而求取待预测结果.

1 物元分析的基本原理和方法

1.1 物元分析的基本原理

对于某一确定事物，可以用有序3元组R= （M，C，X）作为描述该事物的基本单元，称R为物元.其中，M表示事物，C表示特征，X表示M关于C的量值，并将3者称为物元R的3个要素.

如果事物M可以用n个特征C1，C2，…，Cn，以及相应的量值X1，X2，…，Xn来描述，则称为n维物元，记为：

也可以简写为：

式中：C=［C1，C2，…，Cn］T;

X=［X1，X2，…，Xn］T.

1.2 物元分析的方法

物元分析解决问题的基本步骤如下.

（1）确定经典域经典域为：

（2）确定节域节域为：

（3）确定待评估物元待评估物元为：

（4）确定关联函数值关联函数值为：

（5）计算权系数和关联度对于每一个特征参数ci，根据其重要性确定相应的权重系数ωij，并应满足如下条件：

在权重系数和关联函数已知的情况下，可计算待评估对象对第j等级的关联度为：

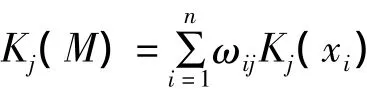
（6）对关联度的分析和评价若Kj=max Kj（M），则说明待评估对象属于第j等级.

2 负荷密度指标物理模型的求取

应用负荷密度指标法进行电力负荷预测时，依据规划区中已知地块性质来分别确定其负荷（密度）指标.本文采用文献［4］中的物理模型，以商业负荷密度指标的求取为例，分析负荷密度指标影响因素，引入物元分析基本理论.通过对大量的样本负荷密度指标的分析可知，影响某类地块负荷密度指标大小的因素是多方面的，通过科学分析认为，作为商业负荷密度指标的主要影响因素有商场定位C1，地理位置C2，结构因素C3.上述3个因素一般是用定性指标（如高、较高等）描述的，不便于各指标之间的比较和运算，为解决上述问题，可采用两级比例方法将定性指标转化为定量指标［4，9］.将具体地块负荷密度指标、3个影响因素及其量值组成物元.调研整理出的部分参考样本（大厦）负荷密度指标见表1.

表1 部分参考样本负荷密度指标

根据样本数据的取值范围，并结合工程经验，将样本划分为5个等级，取每类样本的评价因素取值范围构造5级标准样本指标集，见表2.

表2 5级标准样本指标集

3 物元模型构建及求取

假设待测对象为未知商业建筑M，其定位高但位置一般，建筑面积为21 540 m2，营业面积为11 500 m2，建筑综合能耗较高.下面以M为例，详细介绍应用物元分析求取商业负荷指标的步骤.

3.1 数据的规范化处理

在求取负荷密度指标的过程中，各个指标量化值所在的区间也不完全相同，有些指标越高，负荷密度指标越高;有些指标越低，负荷密度指标却越高.为了便于指标之间的相互比较，需要将各指标量化值进行规范化处理.本文采用文献［10］中提到的方法进行规范化，即：

规范化后的负荷密度指标标准等级界限如表3所示.

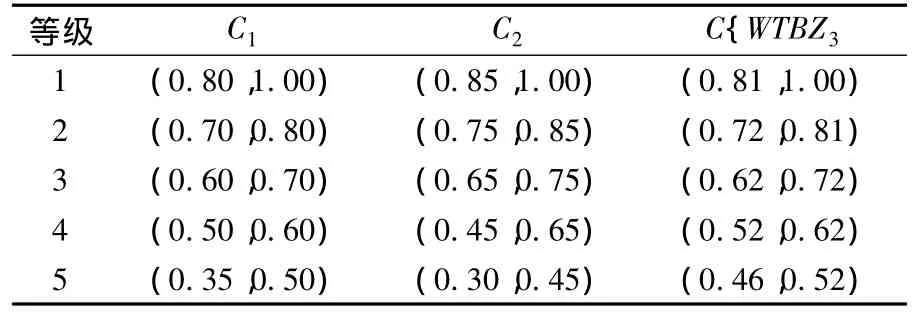
表3 规范化的负荷密度指标等级界限

3.2 确定经典域和节域

根据规范化的负荷密度指标等级界限，可以分别确定经典域Ri（i=1，2，…，5）和节域Rp，即：

3.3 待评估对象的物元

依据待评估对象M的实际情况，可以确定其参数，即：

对R0进行规范化处理，可以得到规范化的物元：

3.4 计算关联函数值

根据关联函数的计算公式可以计算得到相应的关联函数值，其结果如下：

3.5 计算权重系数和关联度

对于负荷密度指标评估等级j的特征Ci对应的权重系数，可以由对应的等级界限阈值求得，权重系数的计算公式［11-13］为：

利用式（1）得到的对应权重系数见表4.

表4 负荷密度指标各等级影响因素权重系数

应用以上运算得到的关联函数值和权重系数，可以得到评估对象M对第j等级的关联度Kj（M）（j=1，2，…，5）.

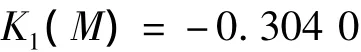
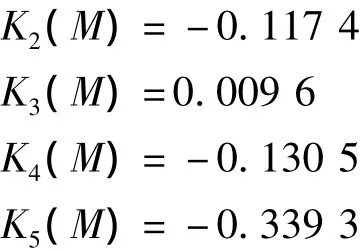
3.6 结果分析

由K3=0.009 6可知，显然待评估对象M属于负荷密度指标第3等级，即负荷密度指标范围为60～80 W·m-2.通过与标准样本的平均密度指标进行抛物线插值［4］，可以得到M的参考负荷密度指标值为79.76W·m-2，与调研得知的该商场实际负荷密度指标77 W·m-2相比较，计算误差约为3.58%，在允许范围内.

为进一步验证算法的适用性和可靠性，本文另选取3个典型商业建筑，应用物元分析求取其负荷密度指标.3个商业建筑的特征原始数据为：建筑3定位高，位置好，建筑面积30 000 m2，营业面积20 000 m2，建筑综合能耗较高，编号为M1;建筑7定位中，位置一般，建筑面积18 000 m2，营业面积11 000 m2，综合能耗一般，编号为M2;建筑9定位较低，位置较差，建筑面积15 068 m2，营业面积12 000 m2，综合能耗较低，编号为M3.

分别对上述3个对象的特征原始数据进行处理，量化后的特征数据见表5.然后对量化数据进行规范化处理，得到的特征量化值如表6所示.

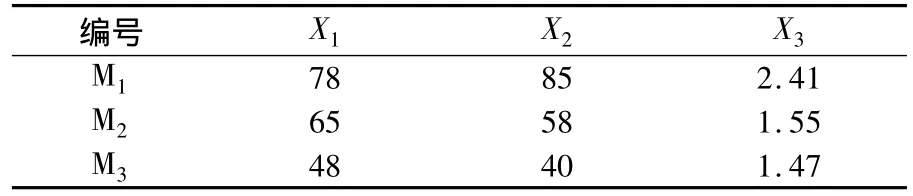
表5 3个对象的特征量化值

表6 3个对象规范化的特征量化值

按照负荷密度指标的求取步骤，可以分别求得3个对象对应的关联度，如表7所示.

表7 3个对象的关联度

由表7可知，M1属于商业负荷指标第2等级，M2属于商业负荷指标第4等级，M3属于商业负荷指标第5等级，与实测数据所在等级相同.

采用抛物线插值函数分别求取3个对象对应的预测负荷指标，依次为99.28 W·m-2，59.24 W·m-2，34.36W·m-2.应用本文提出的负荷密度求取方法分别得到以上4个商业建筑的负荷密度指标，与实测数值之间的误差分析见表8.

表8 4个对象的误差分析

由表8可知，预测结果与实际相比，误差都在5%以内，能够满足工程实际需要，表明物元分析理论应用于求取负荷密度指标是科学可行的.

通过对负荷密度指标预测误差的分析，可以发现误差主要来源于两个方面：一是各影响因素原始数据获取不够准确，对原始数据的预处理有待加强;二是模型本身严密性一般，有待改善.对以上两个方面进一步完善以后，能够提高该方法的预测精度和实用性.

4 结语

本文采用物元分析理论建立了负荷密度指标求取模型.由于数据的处理、关联函数计算及结果的计算通用性较好，样本的经典域和节域物元适用各类规划区，具有较好的适应性和灵活性.计算结果表明，物元分析理论应用于求取负荷密度指标是科学可行的，在实际操作过程中可继续加强影响因素量化方法的研究，进一步提高预测的精度和实用性.

［1］W ILLISH L.Spatial electric load forecasting［M］.New York： Marcel Dekker，1996：13-14.

［2］CHOW M Y，ZHU Jin-xiang，TRAM H.Application of fuzzy multi-objective decision making in spatial load forecasting［J］.IEEE Trans.on Power Systems，1998，12（3）：1 185-1 190.

［3］余贻鑫，张弘鹏，张崇见，等.空间电力负荷预测小区用地分析的模糊推理新方法［J］.天津大学学报，2002，35（2）： 135-139.

［4］符杨，朱兰，曹家麟.基于模糊贴近度理论的负荷密度指标求取新方法［J］.电力系统自动化，2007，31（19）：46-49.

［5］符杨，曹家麟，谢楠，等.基于模糊综合评判的负荷密度指标选取新方法［J］.电网技术，2007，31（18）：19-22.

［6］蔡文.可拓论及其应用［J］，科学通报，1999，44（7）：35-38.

［7］蔡文.物元分析［M］.广州：广东高等教育出版社，1987： 45-50.

［8］蔡文.可拓集与可拓数据挖掘［M］.北京：科学出版社，2008：16-21.

［9］符杨.基于优化决策理论的节约型配电网规划若干关键技术的研究［D］.上海：上海大学机电工程与自动化学院，2007.

［10］丁立，贾秀芳，赵成勇，等.基于可拓学的电能质量综合评价［J］.电力自动化设备，2007，27（12）：44-47.

［11］黄剑，周林，栗秋华，等.基于物元分析理论的电能质量综合评估［J］.重庆大学学报：自然科学版，2007，30（6）：25-29.

［12］迟远英，牛东晓，李向阳，等.基于物元分析理论的供电服务质量评价方法［J］.电力系统自动化，2010，34（13）：33-37.

［13］周凯，栗秋华，周林，等.基于物元分析理论的大电力客户信用评价［J］.电网技术，2009，33（16）：75-80.

（编辑胡小萍）