基于小波包变换的电力系统谐波检测

刘蓉晖

（上海电力学院电力与自动化工程学院，上海 200090）

谐波不仅使电力设备损耗增加，导致继电保护和自动化装置误动作，引起电气谐振和电机的机械振动，而且还会干扰通信线路，影响测量仪表的精度，甚至造成电网的大事故.因此，对电力系统的谐波进行有效治理，具有明显的社会经济效益［1］.谐波检测是实现谐波治理的前提条件，谐波检测已成为当前国内外电能质量检测研究的热点之一.

目前，电力系统中的谐波检测方法大多是基于快速傅里叶变换（FFT）及其改进算法.傅里叶变换具有良好的频域分析和时域无局部化特性，因此只适合稳态谐波的检测.而小波变换方法具有良好的时频局部化特性，很适合检测突变信号和非平稳信号［2］.但小波变换具有对信号频带划分不均匀、对高频信号检测精度不高，以及高频频带宽、低频频带窄的特点.小波包分析可以实现频带的均匀划分，具有比小波变换更好的时频特性和较高的信号检测精度［3］.

1 小波变换

对于任意的函数x（t）∈L2（R）的连续小波变化（CWT）为：

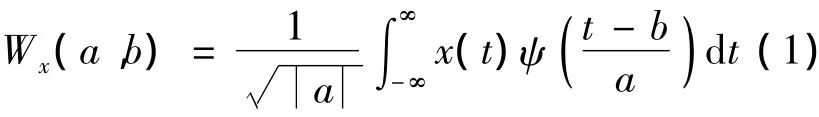
式中：ψ（t ）——基本小波（母小波）;

a，b——小波函数的尺度因子和位移参数，分别决定小波的时频窗在频域和时域的位置.这里的a和b是连续变化的，称为连续小波变换.

小波变换具有对信号的自适应性.在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，所以也被称为数学显微镜［4］.

实际的观测信号都是离散的，而且由于计算机处理的是离散量，所以信号处理中都采用离散小波变换（DWT）.多数情况下是将尺度因子a和位移参数b按2的幂次进行离散.最有效的计算方法是由MALLAT S于1988年提出的基于多分辨率分析的快速小波算法，又称Mallat算法.

Mallat快速小波变换是利用正交小波基将信号分解为不同尺度下的各个分量，其实现过程相当于重复使用一组高通和低通滤波器将信号逐步分解.第一步是将信号分解为通过高通滤波器产生的高频细节分量和通过低通滤波器产生的低频近似分量.低频分量和高频分量所占频带宽度相等，各占信号的一半频谱带.第二步是对低频分量重复上述过程进行进一步分解，从而得到下一层次上的两个分解分量，而高频分量不再进行分解.以下再依此类推分解.由于小波变换对信号频带的划分不是均匀划分，因此信号的低频部分能够得到精确分解，但在高频段的频率分辨率较差.

2 小波包变换

小波包变换是建立在小波变换的基础上的，它可以实现频带的均匀划分，对小波变换中没有细分的高频分量作进一步分解，并能够根据被分析信号的特征，自适应地选择相应频带，使之与信号频谱相匹配，以提高时频分辨率.

2.1 小波包基本原理

设x（t）为待分析时间信号，P（i，j）表示第i层（即尺度因子为2i）上的第j个小波包，称为小波包系数.H和G为小波包分解低通和高通滤波器.小波包分解的快速算法为［5］：

2.2 小波包的频带划分

现有的小波包分解结构，各个频带标记的大小与相应的频带频率大小不完全对应.这样就对谐波的频率分析带来困难，不能根据小波包分解的结果直接判断谐波频率范围，不利于谐波检测分析.文献［6］提出了一种新的小波包分解结构，即将低通和高通滤波器的排列重新调整，就可以得到按频率大小顺序连续分布的均匀频带.若将信号中的最高频率看作是1，进行5层小波包分解，则可将整个信号频带分成连续顺序的32个子频带，每个子频带带宽为1/32=0.031 25.新的小波包滤波器组结构及其频段划分见图1.

待分析信号X经过第1层小波包分解，通过低通滤波器H的信号频带范围为0～0.5，通过高通滤波器G的信号频带范围为0.5～1;将这两组信号进行第2层小波包分解，滤波器组排列顺序依次为低通滤波器H，高通滤波器G，高通滤波器G和低通滤波器H;以此类推.按照图1所示的滤波器排列顺序，经过第5层小波包分解后的32个子频带的频率范围依次为0～0.031 25，0.031 25～0.062 5，…，0.968 75～1，因此不同频带的小波包系数就相当于从某个时-频窗内提取到的原始信号信息.

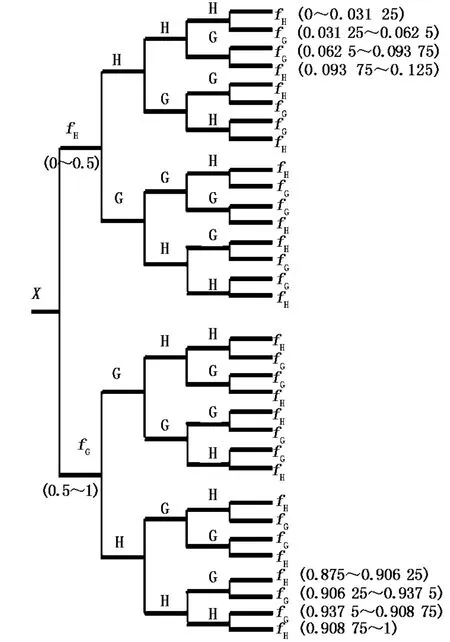
图1 新的小波包滤波器组结构及其频段划分

3 仿真实例验证

3.1 电力系统稳态谐波的检测

以三相桥式整流电路在电感性负载时交流侧的电流作为谐波信号进行检测.该信号为正负半周各120°的近似方波，其数学表达式为：

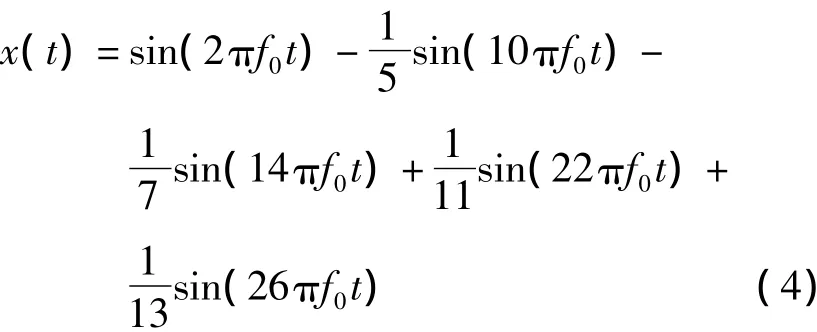
式中：f0=50 Hz，谐波的幅值采用标幺值.此谐波信号中，除了频率为50 Hz的基波之外，还包括5次、7次、11次和13次谐波.下面用Matlab7.4软件提供的小波分析工具箱进行仿真.

本文采用正交小波db40，因为db40小波的分解与重构信号失真度小，具有良好的计算性和时域光滑性.对原始信号x（t）进行5层小波包分解，采样频率为6 400 Hz;每个基波周期采样128点，采样时间为6个基波周期.整个频带分解成25=32个子频带，每个子频带宽1/32×3 200= 100 Hz.原始信号x（t）通过5层小波包分解，被分离到各个子频带中，计算第5层小波包分解系数的重构信号，得到第5层第j个小波包系数的重构信号，小波包分解结点为（5，0），（5，1），（5，2），（5，3），（5，4）（5，5），（5，6），（5，7）的小波包重构信号频率范围及谐波次数见表1.原始信号和重构信号的波形见图2.

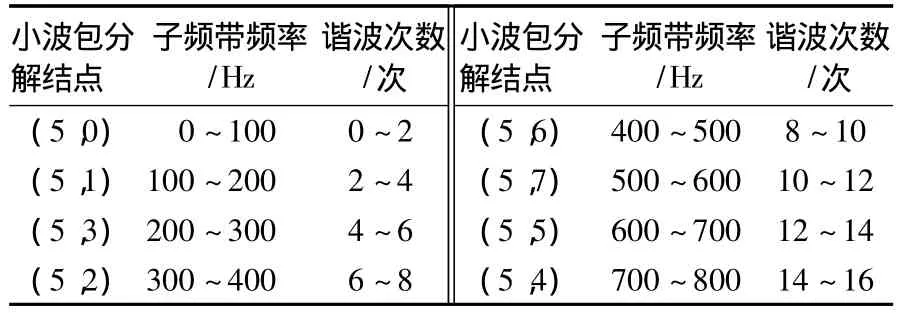
表1 小波包重构信号的频谱范围

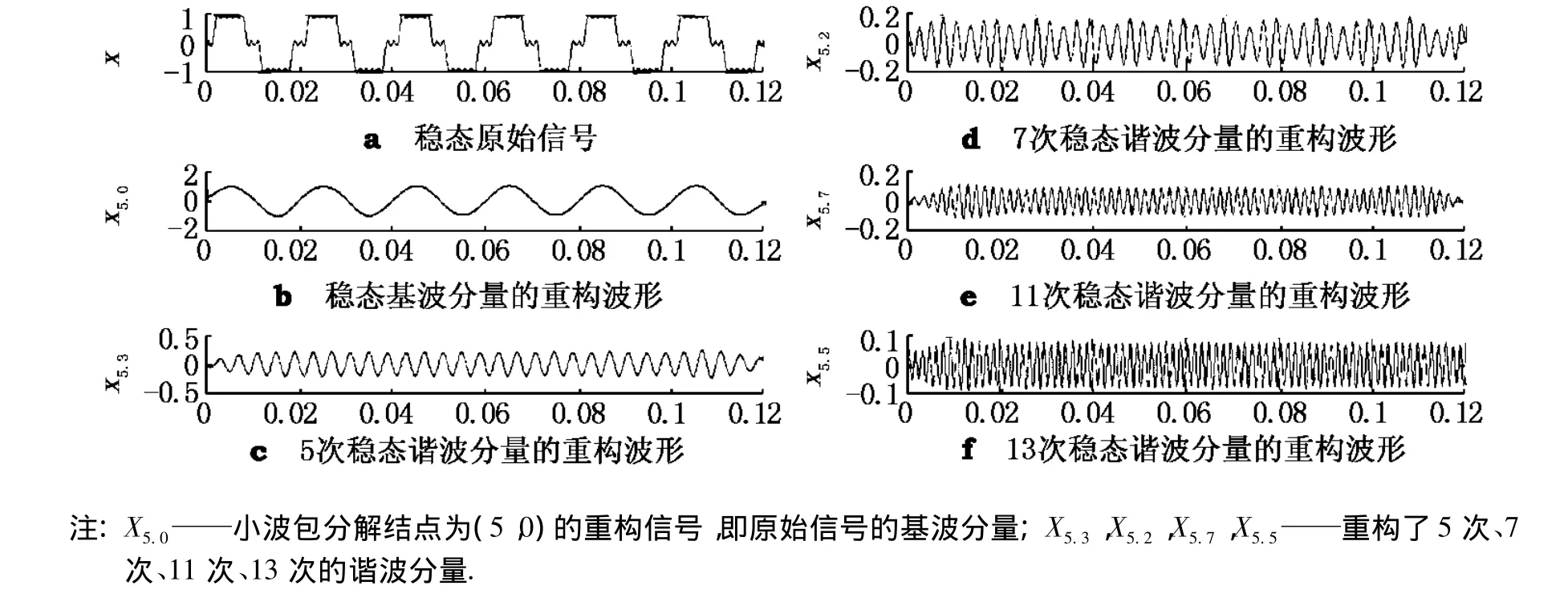
图2 小波包变换对稳态谐波信号的重构波形

由图2可知，所得波形与理论波形相同.由此可见，小波包重构信号可以将原始信号在各个子频带有效分离出来.

3.2 电力系统暂态谐波的检测

某电力系统暂态谐波信号的数学表达式为：

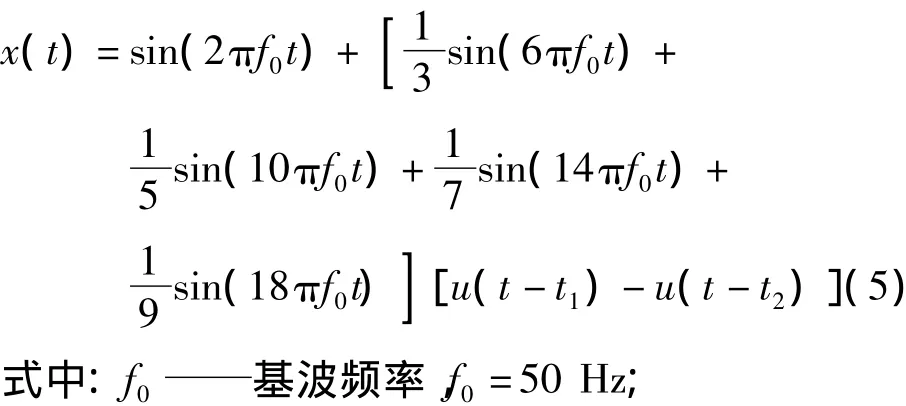
t1起始时间，t1=0.1 s;

t2结束时间，t2=0.2 s.

选用db40小波对原始信号进行5层小波包分解，采样频率为6 400 Hz，采样周期12个.该信号的基波频率为50 Hz，在采样的第6至第10个周期出现了3次、5次、7次和9次谐波.其仿真试验结果见图3.

由图3可知，X5.0完美地重构了原始信号的基波，X5.1，X5.3，X5.2，X5.6重构了原始信号的3次、5次、7次和9次暂态谐波，根据波形可以得到暂态谐波的起止时间分别为t1=0.1 s，t2=0.2 s，与理论值一致.

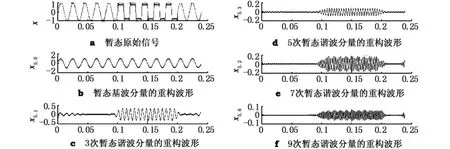
图3 小波包变换对暂态谐波信号的重构波形

4 结论

（1）小波包变换具有良好的时频局部化特性，对信号频带可以实现均匀划分，适用于电力系统谐波的检测.

（2）仿真试验表明，通过小波包变换可对电网中的稳态谐波和暂态谐波进行准确分析，能为电网中谐波的研究和治理提供依据.

［1］任震.小波分析及其在电力系统中的应用［M］.北京：中国电力出版社，2003：12-36.

［2］任震，黄群古.基于多频带小波变换的电力系统谐波分析新方法［J］.中国电机工程学报，2000，11（2）：38-41.

［3］薛惠，杨仁刚，罗红.利用小波包变换实现电力系统谐波分析［J］.电网技术，2004，28（5）：41-45.

［4］胡昌华，李国华，周涛.基于MATLAB 7.x的系统分析与设计小波分析［M］.西安：西安电子科技大学出版社，2008：20-69.

［5］徐剑，金之俭，傅坚，等.基于改进小波包算法的变压器绕组变形的检测［J］.华东电力，2010，38（3）：376-380.

［6］PHAM V L，WONG K P.Antidistortion method for wavelet transform filter banks and nonstationary power system waveform harmonic analysis［J］.IEE Proceedings Generation，Transmission and Distribution，2001，148（2）：117-122.

（编辑胡小萍）