基于ANSYS结构优化模块的加载反力架设计

田文姜，邹 力

(中铁大桥局集团武汉桥梁科学研究院有限公司，湖北 武汉 410034)

对梁、柱等简单构件组成的结构或构件，一般有现成的规范作为设计依据，或结合以往的设计经验来辅助设计，而对于三向尺寸相差不大的板、实体及其组合结构和构件，或其他一些样式独特、没有设计依据的新颖结构，往往缺乏成熟可靠的设计方法。通常需要借助有限元软件来分析和设计，并需多次调整参数以获得理想的设计结果。

1 ANSYS及其结构优化模块简介

ANSYS拥有功能强大的APDL设计语言，它是一种参数化设计语言，使用它可以将大多数设计变量参数化，这为它的优化模块提供接极大便利，也是其优化模块的功能基础。

该模块有三大参数类，即设计变量、状态变量和优化函数。设计变量一般是结构的尺寸、荷载、材料属性等，它们是给定的状态变量，是设计变量的函数，如应力、变形、振动频率等，目标函数则是需要最小化的变量，它也是设计变量的函数，但受状态变量约束(如应力和变形控制)。

ANSYS软件提供了零阶方法和一阶方法是常用的两种。零阶方法属于直接法，通过调整设计变量的值，采用曲线拟合的方法去逼近状态变量和目标函数，该方法适合于大多数工程问题。一阶方法是间接方法，使用了状态变量对设计变量的导数，在每次迭代中梯度计算确定搜索方向。由于该方法在每次迭代中要产生一系列的子迭代，它所占用的时间较多，但其计算精度要高。ANSYS可以将多种优化方法混合使用，为了提高收敛速度，用户可以先采用某种优化方法迭代几次，然后再利用其它方法进行迭代。

2 优化的要点

设计者需要合理地选择设计变量，要根据具体情况综合考虑，尽量挑选对设计结果影响较大的参数，也可试运行优化来研究目标函数对某个设计变量的敏感性。设计变量要尽可能少，各设计变量要相互独立。设计变量总数不能超过60个，一般不超过10个，否则将大大降低优化效率。

状态变量要对设计变量形成足够和有效的约束，一般选为应力、变形、频率等。随着设计变量的改变，状态变量的最大值或最小值发生的位置也可能在变化，因此往往需要定义几个关键部位或关键构件的应力、变形或频率等。

设计变量和状态都需要指定合适的容差，以控制迭代在什么情况下终止。实践表明，容差对优化结果有明显影响，所以设计者需要对容差做试探性调整，对不同容差产生的优化结果进行比较，这是一个实践性较强的操作。

优化开始之前，需要给各设计变量赋一个初始值，这个初始值对优化结果有明显影响，它可能使优化结果收敛于一个局部极小值，也可能会导致优化过程耗费大量时间而得不到可行的设计序列。因此，为了提高优化效率，一般需要先采用适当的优化工具来搜寻和研究设计域。ANSYS优化模块提供的优化工具有随机搜索法、等步长搜索法、乘子计算法、最优梯度法等。例如，用搜索工具初步得到一些较好的设计序列，缩小设计空间，排除一些局部最小值;采用扫描工具可以确定哪些设计变量对目标函数的影响较为明显，据此可以对这些变量指定更严格的收敛容差。

以上准备工作做好后，即可采用零阶方法作优化，一般均可得到较好的优化结果。如果对优化结果不满意，可再采用一阶方法，但一阶方法未必可以得到更好的结果，或其优化过程耗时太长而失去优势。

3 试验反力架的优化步骤和结果

某模型试验对一座斜拉桥索塔的一个节段进行顶推加载试验，需设计一套反力架。荷载作用在反力架两端斜面上，各斜面上均作用法向力3500 kN。为得到一个合理设计，节约钢材，现用ANSYS的结构优化设计模块对该反力架进行优化设计(图1)。

反力架各板件均为Q345钢材。因模型高度、加载所用的千斤顶高度和加载坡面的角度均已确定，故反力架外形尺寸也确定，各部位尺寸见图1。立柱为纯受拉构件，不参与优化。需要调整优化的参数为各板件厚度ti(i=1，2，…，9)和横梁高度 h，即设计空间为(t1，t2，…，t9，h)T，其中各板初始厚度均取10mm，横梁高度取100mm。各板厚度下限值需根据整体稳定及局部稳定要求逐一确定。

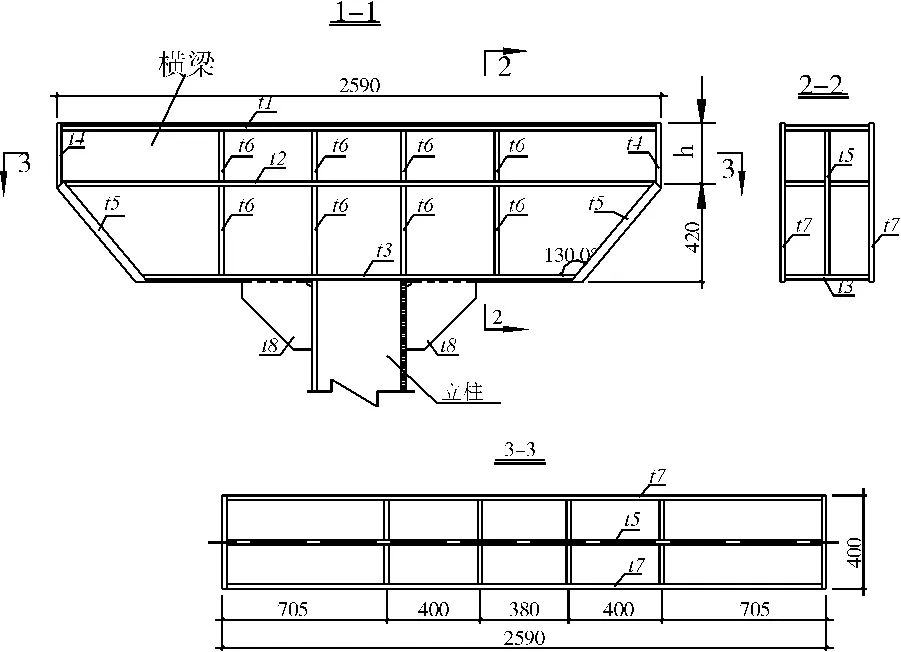
图1 反力架形状和尺寸(单位:mm)

取板件的Von Mises应力值作为状态变量。根据多次试算发现，应力最大区域为横梁顶板中间处、中腹板两端及底板靠近三角形加劲板处。取这三处Von Mises应力值作为状态变量，分别记为 σ1、σ2、σ3，并统一限定其应力上限均为280MPa。取所有板件总体积作为目标函数，该目标函数最小值对应的设计序列即为本反力架的最优设计。

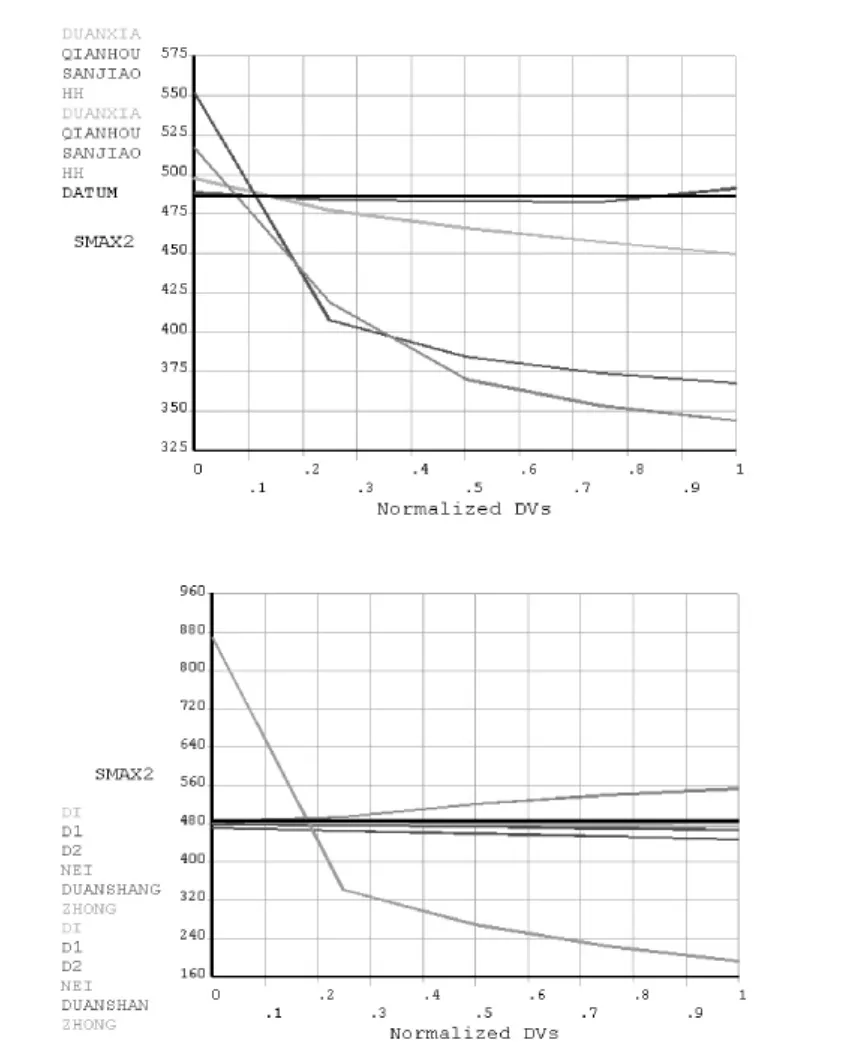
图2 状态变量σ2对各设计变量的敏感度

(1)运行扫描工具，以考察各设计变量对所关心区域应力值的影响。通过简单设置并运行，即可得到图2所示的DV－SV曲线，知腹板Von Mises应力σ2对各设计变量的敏感性。由计算结果知，中腹板厚度、梁高对顶板应力影响最为明显，梁内横隔板厚度对底板应力最为明显，梁高和横隔板对腹板应力影响最为明显。同样，可以得到各设计变量对顶板应力、底板应力和目标函数的影响程度。根据以上分析，可以有针对性地设置设计变量的取值范围，对状态变量和目标函数影响大的设计变量要指定较大的设计范围，影响小的设计变量的设计范围可适当缩小，以提高优化效率。

(2)运行随机搜索工具，设定的目标是随机得到200个设计序列或100个可行设计序列。运行结束后，实际得到124个设计序列，其中100个为可行设计，可行设计中最优设计对目标函数为0.385 m3，该值给随后的进一步优化的目标函数的提供了一个上限值，即以后凡目标函数大于该值者皆非最优设计。随机搜索得到的一系列结果还可以作为分析设计变量与目标函数关系的依据。

(3)执行零阶优化。执行之前需设定最大迭代次数和允许的不可行设计序列数量，程序默认值分别为30和7。在本次优化中，分别使用100、30和200、30，两次优化结果相差微小，故可认为优化结果比较理想。优化得到的部分设计序列见表1，其中带“*”者即90号序列对应最佳设计，其对应的设计参数t1，t2，…，t9(限于篇幅表中未列)并非整数，可根据材料选取的可行性，将其数值适当向上取整。

?

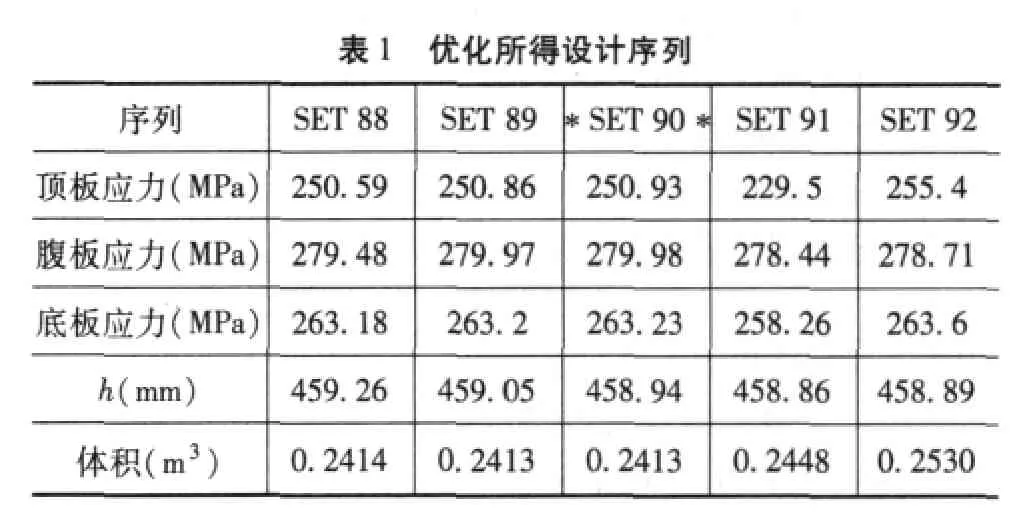
通过优化工作，不仅保证了该反力架的强度，还得到了合理的设计参数，实现结构的轻型化，节约了材料。

4 结束语

在一些特殊结构(如本文的反力架)或重要结构的设计中，在构件截面尺寸、结构的形状和选材等问题上，尤其是涉及细部构造时，设计者往往缺乏经验，很难同时保证安全和经济。在这种情况下，通常需要采用结构优化设计方法。

在结构优化设计的诸多方法中，选出实用且简便的一种或几种，是广大结构设计者的共同愿望，本文采用的方法即为这样一种方法。该方法使用现成的通用有限元软件，不涉及过于复杂的数学运算，且可以通过APDL语言完成整个设计过程，操作简便，设计者乐于接受。

［1］汪树玉，刘国华，包志仁.结构优化设计的现状与进展［J］.基建优化，1999，20(4)

［2］Design Optimization，Release 10.0 Documentation for ANSYS

［3］钱倩.基于有限元分析的轻钢结构优化设计研究［J］.山西建筑，2008，34(7)

［4］戴国欣.钢结构［M］.武汉:武汉理工大学出版社，2007