Local Wave Applied to Detect and Characterize Acoustic Emission Signals
LIN Li,
(School of Naval Architecture,Dalian University of Technology,Dalian 116023,China)
1 Introduction
Acoustic emission(AE)[1]is defined as the class of phenomena whereby transient elastic waves are generated by the rapid(and spontaneous)release of energy from a localized source or sources within a material,or the transient elastic wave(s)so generated.This energy travels through the material as a stress or strain wave and is typically detected using a piezoelectric transducer,which converts the surface displacement(vibrations)to an electrical signal.The signal is usually amplified and transmitted,and then sent to the computer via the analogueto-digital(A/D)converter.The characterization of defects in materials can be found by processing the acoustic emission(AE)signals.The key to the problem is how to analyse AE signals using an effective tool.
Various approaches have been used to analyse AE signals,such as the Fast Fourier transform(FFT)method and the wavelet transform method.The Fast Fourier transform(FFT)is designed to work with linear and stationary signals.A disadvantage of the FFT method is that it provides a solution only in the frequency domain;it cannot be used in the time domain.The wavelet transform,on the other hand,is non-adaptive nature.Once the basic wavelet is selected,one will have to use it to analyze all the data.Since the most commonly used wavelet is Fourier based,it also suffers the many shortcomings of Fourier spectral analysis.Versatile as the wavelet analysis is,the problem with the most commonly used Morlet wavelet is its leakage generated by the limited length of the basic wavelet function,which makes the quan-titative definition of the energy-frequency-time distribution difficult.Sometimes,the interpretation of the wavelet can also be counterintuitive.
This paper investigates the effectiveness of a new time-frequency analysis method designated as Local Wave Analysis(LWA)for analyzing the nonstationary acoustic emission signals.This method based on local wave decomposition(LWD)and Hilbert transform is suited for analyzing nonlinear and non-stationary data and this decomposition method is adaptive,and,therefore,highly efficient.The advantage of LWD is its ability to adaptively decompose an arbitrary complicated time series into a set of components,called intrinsic mode functions(IMFs),which has particular physical meaning.By decomposing the time series into IMFs,it is flexible to perform the Hilbert transform to calculate the instantaneous frequencies and to generate effective time-frequency distributions called Hilbert spectra.The effectiveness of the proposed methods has been demonstrated by the acoustic emission signals from the steel tube cracking during a quasi-static loadings test.The cracking could be identified by applying local wave analysis to AE signals.The evolution of specific AE local wave parameters like the Hilbert spectrum is suited to identify the cracking.Firstly,LWD method is used to decompose the acoustic emission signal into a number of intrinsic mode functions(IMFs).The IMFs are able to adaptively separate the characteristic frequencies.The characteristic frequency components,which were extracted from these IMFs,provide the acoustic emission information.Then,we identify the acoustic emission characteristic in the Hilbert spectrum,which is an energy/frequency/time distribution.When acoustic emission occurs the Hilbert spectrum energies of the associated characteristic IMFs change,which is different from the effect of changes of the other conditions e.g.background noises.In particular,signals due to cracking and non-cracking could be neatly separated.Consequently,the experimental results show that the proposed approach is not only able to effectively capture the significant information reflecting the acoustic emission,but also reduces the sensitivity to the effect of various uncertainties,and thus has good potential in the field of acoustic emission signal feature extraction.
2 Local Wave Decomposition method[2-3]
Local Wave Decomposition(LWD)method is a new method,developed by Huang et al in late 1990’s,for analyzing nonlinear and non-stationary signals,which is developed from the simple assumption that any signal consists of different simple intrinsic modes of oscillations.They suggest a practical way to decompose the data so that the components all satisfy the conditions imposed on them.Physically,the necessary conditions for us to define a meaningful instantaneous frequency are that the functions are symmetric with respect to the local zero mean,and have the same numbers of zero crossings and extrema.Based on these observations,we propose a class of functions designated as intrinsic mode functions here with the following formal definition.
An intrinsic mode function(IMF)is a function that satisfies two conditions:
(a)In the whole data set,the number of extrema and the number of zero crossings must either equal or differ at most by one.
(b)At any point,the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero.
An IMF represents a simple oscillatory mode compared with the simple harmonic function.With the definition,any signal x(t)can be decomposed as follows:
(1)Identify all the local extrema,and then connect all the local maxima by a cubic spline line as the upper envelope.
(2)Repeat the procedure for the local minima to produce the lower envelope.The upper and lower envelopes should cover all the data between them.
(3)The mean of upper and low envelope value is designated as m1,and the difference between the signal x(t)and m1is the first component,h1,i.e.

Ideally,if h1is an IMF,then h1is the first component of x(t).
(4)If h1is not an IMF,h1is treated as the original signal and repeat(1),(2)and(3);then

After repeated sifting,i.e.up to k times,h1kbecomes an IMF,which is

Then it is designated as

The first IMF component is obtained from the original data.c1should contain the finest scale or the shortest period component of the signal.
(5)Separate c1from x(t):We get

where r1is treated as the original data and repeat the above processes.The second IMF component c2of x(t) could be got.Let us repeat the process as described above n times.Then n-IMFs of signal x(t) can be got.Then,

The decomposition process can be stopped when rnbecomes a monotonic function from which no more IMFs can be extracted.By summing up Eqs.(5)and(6),we finally obtain

Thus,one can achieve a decomposition of the signal into n-empirical modes and a residue rn;which is the mean trend of x(t).The IMFs c1,c2,…,cninclude different frequency bands ranging from high to low.The frequency components contained in each frequency band are different and they change with the variation of signal x(t),while rnrepresents the central tendency of signal x(t).
Having obtained the intrinsic mode function components,we will have no difficulties in applying the Hilbert transform to each component,and computing the instantaneous frequency.After performing the Hilbert transform on each IMF component,we can express the data in the following form:

Equation(8)enables us to represent the amplitude and the instantaneous frequency as functions of time in a three-dimensional plot,in which the amplitude can be contoured on the frequency-time plane.This frequency-time distribution of the amplitude is designated as the Hilbert amplitude spectrum,H(ω,)t,or simply Hilbert spectrum.If amplitude squared is more desirable commonly to represent energy density,then the squared values of amplitude can be substituted to produce the Hilbert energy spectrum just as well.
3 Local wave analysis of simulated AE signals
We can describe[4]an AE signal by a series of wavetrains of the same form,but of different amplitudes and varying time of occurrence.By the expression:

where viand tiare the amplitude and time of occurrence,respectively,for the ith burst,and g(t)is the assumed waveform of a single burst.It is often assumed that g(t)is a damped sinusoidal oscillation which can be expressed by the function:

where f0is the resonant frequency of the transducer,andτis the characteristic decay time.
In order t o obtain an AE signal,wefurther simulate random impulses from which the bursts originate.We can express x(t)as:

here x(t)is a transient signal which has two different time of occurrence and two different modulate frequencies.Fig.1 shows the waveform.Its FFT result is shown in Fig.2.The peak frequency is about 40Hz and 20Hz.

Using the FFT analysis,we can identify the frequencies information.However,the time information about peak frequencies and the relationships between them for each AE signal is unknown.So,it is necessary to develop a time-frequency analysis to understand which AE is prior to the other or how long the AE at a microcrack remains in a fracture process.Here,we use the LWD(Local Wave Decomposition)to obtain time-frequency information for each AE signal.
After LWD is applied to the simulation AE signal,the simulation AE signal is decomposed into 8 IMF components,c1-c8 which include different components from lower to high frequency,and a residue which can be either the mean trend or a constant in Fig.3.The Hilbert spectrum in the colour map format for the AE signal is given in Fig.4.This spectrum gives a weighted appearance in comparison with the corresponding wavelet spectrum shown in Fig.5.The exact occurrence time(2s and 8s)and the corresponding Fourier spectrum(40Hz and 20Hz)of that AE oscillation are given in the full Hilbert spectrum.However,as we can see in Fig.5,there exist the leakages generated by the limited length of the basic wavelet function.In fact,the Hilbert spectrum is a weighted non-normalized joint amplitudefrequency ime distribution.So,we can try to apply the Local wave method to the AE signal processing.


4 Applications of LWA in acoustic emission signals processing
A 2m long steel tube sample was used in this study.A schematic diagram of the experimental set-up is shown in Fig.6.The used detection system was soundwel waveform acoustic emission system(SDAES)from Soundwel Technology(Beijing)Corporation.Two piezoelectric sensors(SR150A),with frequency band 50-400kHz,were coupled to the surface of the steel tube by vacuum grease.Then signals passed through pre-amplifiers(PAI)and were measured by means of the main data acquisition board(SDAE-5)based five-channel A/D system with a sampling rate of 2.5MHz.Soundwel application software(SDAES-V6.3)was utilized to acquire the raw data and perform basic data processing.In the present paper,the signals from the cracking steel tube during quasi-static loadings were collected and stored on a computer to extract the features by using the local wave analysis method.

Fig.7 is the no cracking waveform of a signal picked up just before the steel tube cracked.Fig.8 gives the cracking waveform of a signal obtained while the steel tube was cracking.Fig.9 and Fig.11 show the IMFs and the Hilbert spectrum of the no cracking signal obtained by using the local wave decomposition.Fig.10 and Fig.12 give the IMFs and the Hilbert spectrum of the cracking signal also getting from using the local wave decomposition.

As it is displayed in Fig.9 and Fig.10,after the decomposing,we obtained nine intrinsic mode functions and a residue.The IMF1 of the cracking AE signal(Fig.10)is different from the one of the no cracking AE signal(Fig.9).The IMF1 represents the main oscillation mode and its frequency is 260kHz.
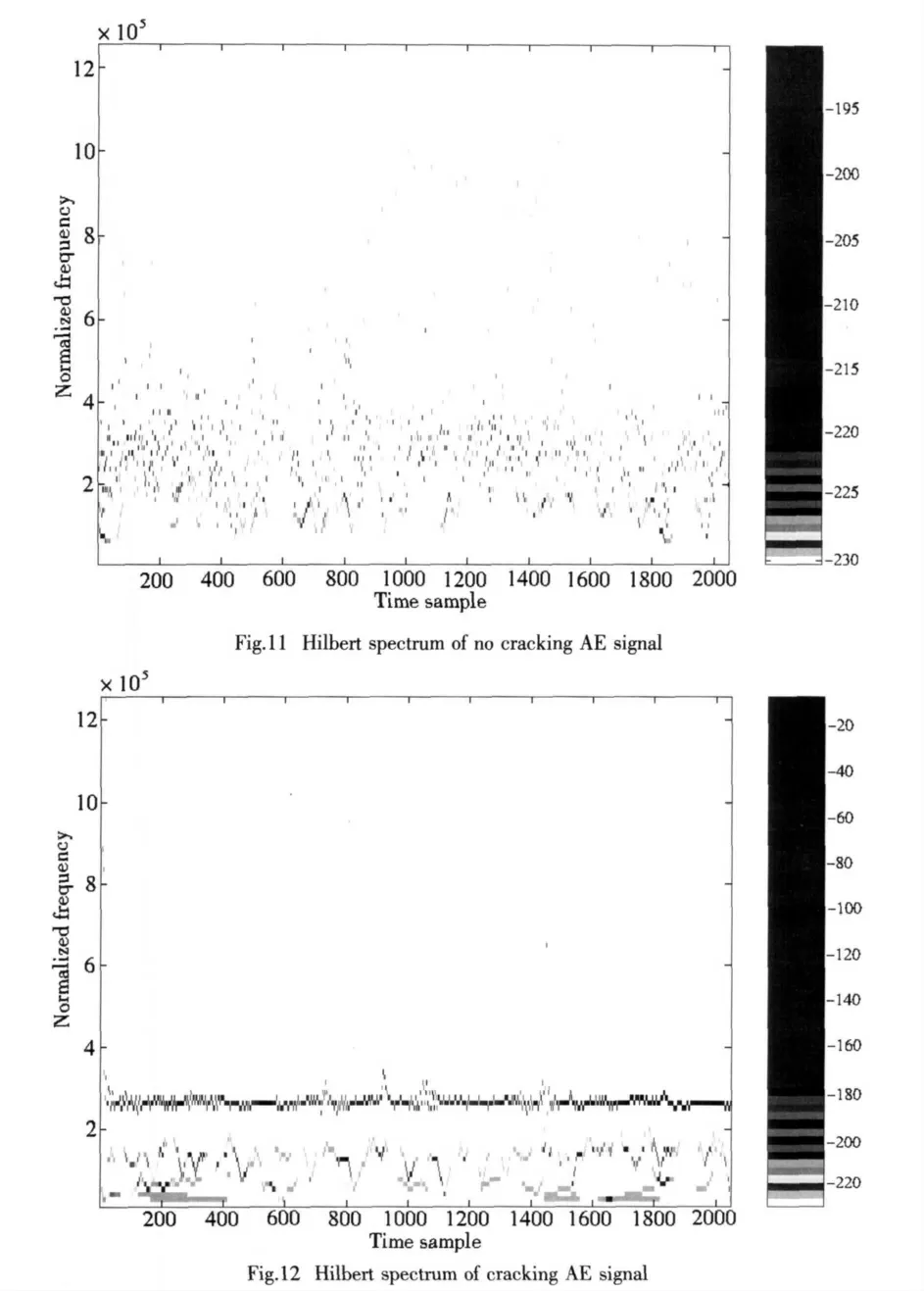
As we can see from Fig.11 and Fig.12,the energy of the cracking AE signal is larger than the energy of the no cracking AE signal.And the energy of the cracking AE signal mostly centers near 260kHz frequency,and the little energy belonging to low frequency.These features indicate clearly the existence of acoustic emission(AE)that is the class of phenomena where-by transient elastic stress waves are generated by the rapid release of energy from localized sources within a material.This will be the reason why the energy at the peak frequency of 260kHz,corresponding to the failure mode of cracking,has a larger value than that for no cracking.
5 Conclusion
One of the most complex problems for acoustic emission(AE)is the extraction of the signal features.In this paper,we applied the Local wave analysis method to extract the features from the acoustic emission(AE)signals.The Local wave analysis provides a new method for time-frequency analysis and has received great attention in various areas.The experimental results of this paper show that this method is effective to identify the cracking by inspecting the relative energies of characteristic frequencies in Hilbert spectra generated based on LWD,and the LWD is able to adaptively separate the characteristic frequency IMF components which form the characteristic components reflecting the process conditions of the steel tube.And thus the local wave analysis method has good potential for the acoustic emission signal processing.
[1]Drummond G,Watson J F,Acarnley P P.Acoustic emission from wire ropes during proof load and fatigue testing[J].NDT&E International,2007,40:94-101.
[2]Huang N E,Shen Z,Long S R,Wu M C,Shih H H,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.Roy.Soc.London.A,1998,454:903-995.
[3]Yu Dejie,Cheng Junsheng,Yang Yu.Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings[J].Mechanical Systems and Signal Processing,2005,119:259-270.
[4]Mitakovi D,Grabec I,Sedmark S.Simulation of AE signals and signal analysis systems[J].Ultrasonic,1985,23(5):227-232.
- 船舶力学的其它文章
- An Overview of Verification and Validation Methodology for CFD Simulation of Ship Hydrodynamics
- Numerical Calculation on the Influence of the Slot Size of Air Injection on Micro Bubbles Drag Reduction for Transitional Craft
- Application of Particle Swarm Optimization Theory in the Hydrofoil Design
- CFD Simulation of the Unsteady Performance of Contra-Rotating Propellers
- Application of Wavelet Denoising in the Modeling of Ship Manoeuvring Motion
- Vibration of Cracked Plates under Tensile or Compressive Load

