CFD Simulation of the Unsteady Performance of Contra-Rotating Propellers
ZHANG Tao,YANG Chen-jun,SONG Bao-wei,CHEN Yan-yong
(1 School of Marine Engineering,Northwestern Polytechnical University,Xi’an 710072,China;2 The 705th Research Institute Kunming,CSIC,Kunming 650118,China;3 School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200030,China)
1 Introduction
Consisting of two sets of coaxial blades which rotate in opposite directions,the Contra-Rotating Propellers(CRPs)have been used principally for propelling torpedoes due to the fact that they can be designed to produce minimal unbalanced torque.On the other hand,the CRPs are superior in efficiency to single propellers since the rotational energy left behind the forward propeller can be almost fully recovered by the aft propeller.Application of the CRPs to commercial ships is quite limited mainly due to the mechanical complexity of the driving shaft system and subsequently the high costs for manufacture and maintenance.In recently years,an alternative solution is provided by using the so-called hybrid CRP podded propulsor which combines a conventional shaft-driven propeller and a puller-type podded propulsor.In this configuration the two propellers are designed to be co-axial and contra-rotating,while driven by a prime mover and an electric motor,respectively.As the requirement for energy saving and low emission intensifies,the CRP concept is expected to receive increasing atten-tion in the future.
The hydrodynamics of CRPs is more complicated than that of a single propeller because of the interaction between forward and aft propellers.This interaction is of periodical nature even if the CRPs operate in the open water,which implies that the hydrodynamic performance of CRPs is always unsteady.So far as the propulsive performance is concerned,only the steady forces and moments are needed.In physical experiments it is straightforward to obtain the steady performance by taking the time-averages of unsteady thrusts and torques.If one chooses to predict the steady performance numerically,however,there exist different approaches.The simplest one is the so-called quasi-steady approach where the flow is assumed to be steady at arbitrary instant.Using this approach the solution is apparently dependent on the relative phase angle between the forward and aft blade sets.Otherwise the unsteady interaction can be time-averaged so that it is circumferentially uniform for both the forward and aft propellers.It is most accurate to use a formulation which accounts for the unsteady interaction and obtain the steady performance by time-averaging the unsteady forces and moments.
Since the 1960’s,a number of methods have been published for predicting both steady and unsteady performances of the CRPs,where the steady and unsteady lifting-surface models[1-3]and steady surface panel model[4]were adopted.All of these methods fall into the category of the potential flow theory,and it appears that the unsteadiness of interaction does not have any appreciable influence on the steady performance at least for the combinations of blade numbers computed in Ref.[3].
Since the late 1990’s,the application of CFD in marine hydrodynamics has been increasing steadily owing to the rapid improvement in both software and hardware capabilities.The use of unstructured mesh generators and flow solvers in many CFD software packages makes it relatively easy to predict the open-water performance of a single propeller by solving the RANS equations,see Refs.[5-7]for example.At the price of consuming much more computational resources,one can expect more accurate results especially at heavy loading conditions by CFD than by potential flow methods mainly because for the latter ones it is difficult to model nonlinear wake deformation and flow separation due to heavy loading.For the CRPs,an additional difficulty arises from the interaction between forward and aft propellers.Specifically,this includes the impingement of forward propeller’s trailing vortices with,and the blockage effect of the aft propeller.It is expected that using RANS simulation the accuracy of performance prediction for CRPs can be improved for both design and off-design conditions.As a part of a series study the authors conducted quasi-steady simulation for two sets of CRPs designed for underwater vehicles using the Multiple Reference Frame(MRF)model[8].Compared with experimental data,the errors in predicted open-water performance were found to be less than 5% at and near design conditions.The influence of phase angle between forward and aft propeller blades when using the MRF model was found to be around 0.5% of the average thrust and torque for both combinations of blade numbers 7-5 and 5-4(forward-aft).In conclusion,the MRF model was found to be an efficient and reasonably accurate tool for evaluat-ing at the preliminary design stage the open-water performance of CRPs with practical combination of blade numbers.
In the present paper,the unsteady interaction between forward and aft propellers is treated strictly by using the Sliding Mesh(SM)model.Numerical simulations are carried out for two sets of CRPs with different combinations of blade numbers and operating in open-water condition.The time-averages of predicted unsteady thrust and torque are compared with their experimental counterparts.The effect of unsteadiness in forward-aft blade interaction is investigated through comparison of results obtained from the quasi-steady MRF and unsteady SM models.It is found that the unsteady model yields more accurate time-averages and fluctuation amplitudes in both thrust and torque because it takes into account the impingement of the forward propeller’s trailing vortex on the aft propeller.
2 Numerical modeling approach
The flow around CRPs operating in the open water is simulated under the assumption that the water is incompressible and viscous.The problem is governed by laws for mass and momentum conservation.Since for practical applications the flow falls into turbulent regime,the Reynolds-Averaged Navier-Stokes(RANS)equations are solved with additional equations which model the transport of turbulent quantities,such as the turbulent kinetic energy and its dissipation rate when the k-εturbulence model is used,and ensure that the set of governing equations are in closed form.The governing equations are not listed here since they can be found in many textbooks,such as Refs.[9]and[10].
As illustrated in Fig.1,a cylindrical portion of the flow field which surrounds the CRPs co-axially is taken as the computational domain.It extends 4DFupstream of the forward propeller disk and downstream of the aft propeller disk respectively,and has a diameter of 5DFwhere DFis the diameter of the forward propeller.This domain is divided into eight sub-domains in order that the most appropriate mesh type can be applied to ensure the best quality and the smallest quantity of discretized cells.As the blades of each propeller are axisymmetrically attached to the hub,each sub-domain is further divided into Z portions of identical geometry,where Z is the number of the forward(or aft)propeller blades.By this further division it is possible to ensure that the cell distributions in all of the Z portions which belong to the same sub-domain are identical to each other when using prismatic or hexahedral cells,or close to identical when using tetrahedral cells.The sub-domains A and E are discretized with tetrahedral cells,B and F with prismatic cells,and the rest with hexahedral cells.

To account for the opposite rotating directions of the forward and aft propellers,sub-domains A through D and E through H are defined,respectively,in a coordinate system rotating synchronously with the forward and aft propeller.Since the clearance between the hubs of forward and aft propellers is not modeled in the present research,the plane marked‘S’in Fig.1 represents two doughnut-shaped faces of identical geometry,overlapping each other but rotating in opposite directions.These faces are defined as sliding interfaces between which flow quantities such as velocity,pressure,and turbulent energy are cross-updated.As shown in Fig.1,the‘inlet’and‘far’boundaries are defined as velocity inlets,while the‘outlet’boundary as pressure outlet.In the rotating coordinate systems,the blade and hub surfaces are defined as stationary walls.Numerical simulations are carried out by using the software FLUENT and the following options:
(1)Solver:pressure based;
(2)Unsteady formulation:2nd-order implicit;
(3)Pressure-velocity coupling:PISO(unsteady),SIMPLE(quasi-steady);
(4)Discretization schemes:Presto!for pressure,2nd-order upwind for momentum and kεequations;
(5)Turbulence model:RNG k-εmodel,standard wall function.
3 Results and discussions
Two sets of CRPs are selected for the present study.Model A[11]consists of two four-bladed propellers which is ideal for studying the forward-aft propeller interactions,though not recommendable for practical purpose.Featuring large tapered hubs,Model B was designed for use with high-speed underwater vehicles.The main geometrical particulars of the models are listed in Tab.1.

Tab.1 Geometrical particulars of CRP models
For Model A,the total number of cells is 4 201 557 for the whole domain in which there are 3 355 677 cells in sub-domains A and E which surround the forward and aft propeller blades and hubs respectively.For Model B,there are 5 576 789 cells in total in which 4 437 969 cells are in sub-domains A and E.
To be consistent with the conditions of open-water tests,the rotational speeds of 720r/min and 600r/min are used in the computations for Models A and B respectively,and the advance speed is varied to reach at different operating conditions.
The time step size is determined byΔt=0.002 5n-1,where n is the rate of revolution per second.This step size corresponds to 0.9 degrees of advancement in blade angular position each time step,and the angular difference between the forward and aft propeller blades will increase by 1.8 degrees each time step.This time step size is determined based on two aspects of consideration.One is to ensure the time accurateness of the solution,i.e.the residuals become small enough after a limited number of iterations for each time step,although it is difficult get them converged.The other is that the time step size should be so small that there are enough data points to resolve the fluctuations in shaft forces and moments.
Consisting of two propellers of the same number of blades,Model A has an interesting feature that,in the open water or an axisymmetrical inflow and when both propellers rotate at the same speed,the loading distributions on all blades of either forward or aft propeller are identical at any instant.When both propellers rotate by 45 degrees the thrust and torque of each propeller repeat themselves,indicating that the thrust and torque both fluctuate at 8 times the shaft frequency and its multiples.In fact,the frequencies at which the thrusts and torques of CRPs fluctuate are determined by f=n (mFZF+mAZA)and subject to mFZF=mAZA,where ZFand ZAare the blade numbers of the forward and aft propellers respectively,mFand mAare integers.When ZF=ZA=4,the lowest frequency appears at mF=mA=1,i.e.fmin=8n.For Model A the 0.9-degree interval is more than enough since there are 50 data points within 1/8 of a revolution,or 45 degrees.Theoretically at least 5 data points are needed to re-construct a period of fluctuation,which means that the 0.9-degree interval is able to resolve fluctuations of up to 80 times the shaft frequency.For Model B,however,the lowest frequency of shaft forces and moments is 70 times the shaft frequency,therefore the 0.9-degree interval is just enough to resolve fluctuations at the lowest frequency.It will be shown in Section 3.2 that it is very difficult to simulate the force and moment fluctuations at such a high frequency since their amplitudes are very small and easily contaminated by non-periodicity in the computational grids.
For each time step a maximum of 20 iterations are used,which is a compromise between computational time and accuracy.As the main purpose of this work is to study the unsteady performance of CRPs,the criterion for convergence is set to be that the maximum relative differences in the thrust and torque of each blade for two consecutive revolutions do not exceed 0.5%.It was found that three complete revolutions are sufficient to fulfill the criterion for both models and operating conditions computed.
3.1 Model A
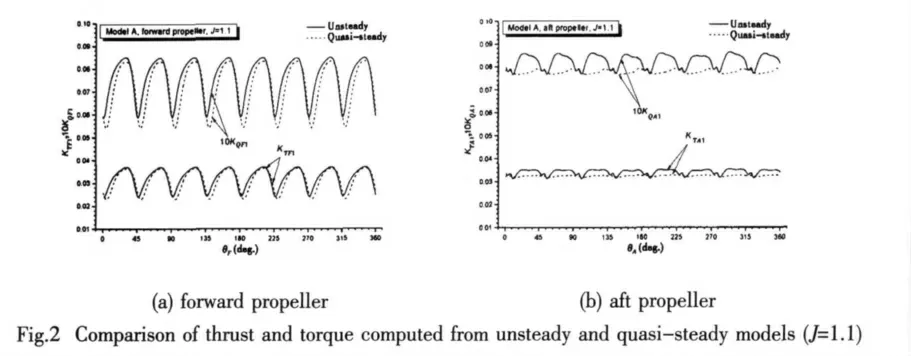
Fig.2 shows the fluctuating thrust and torque of one blade,KTF1,10KQF1,KTA1,and KQA1,obtained from unsteady(SM)and quasi-steady(MRF)simulations for J=1.1.The subscript 1 indicates one blade,while F and A indicate the forward and aft propellers respectively.Note that,throughout this paper,the thrust and torque coefficients as well as the advance coefficient J are based on DF,the diameter of the forward propeller.It is clear from Fig.2 that the thrust and torque both fluctuate at the base frequency as discussed before.On the forward propeller the amplitudes of thrust and torque fluctuations are larger than those on the aft propeller.The differences between unsteady and quasi-steady results are small for the forward propeller,however very large for the aft propeller in both fluctuation amplitudes and time averages.There is a main and a secondary fluctuation seen in Fig.2(b),which is probably caused by the encounter and departure between the forward propeller’s trailing vortex sheets and the aft propeller blades.
In Fig.3 the amplitudes of thrust and torque at 8 and 16 times of the shaft frequency obtained from unsteady simulations are compared with their experimental counterparts for J=0.7,0.9,and 1.1.In general both thrust and torque fluctuations are underpredicted.At 8 times the shaft frequency the errors in computed amplitudes range from 10% to 35%.At 16 times the shaft frequency the errors further increase to about 60% for the forward propeller,and up to 90% for the aft propeller.The primary source of error is considered to be the insufficiency in mesh resolution since in the present simulation there are only about 439 000 and 399 000 cells in sub-domains A and E respectively.
In Tab.2 and Fig.4,the open-water performances obtained from unsteady(SM)and quasisteady(MRF)simulations are shown and compared with experimental data[11].The thrust and torque are time-averaged values in the unsteady case and,in the quasi-steady case,averages of the thrusts and torques obtained at 4.5° intervals over a range that each propeller rotates by 45°.Note that KTM=(KTF+KTA)/2 and KQM=(KQF+KQA)/2.For the forward propeller,the thrust is slightly over-predicted and the torque under-predicted with-6.1% maximum error in the unsteady case and-8.4% maximum error in the quasi-steady case.For the aft propeller,the torque is slightly over-predicted and the thrust under-predicted with-10.2% maximum error in the unsteady case and,in the quasi-steady case,the thrust and torque are both under-predicted with up to-17.8% maximum error.As a result,the error in predicted open-water performance is much smaller by unsteady simulations than by quasi-steady simulations.


Tab.2 Comparison of the open-water performance of Model A obtained from unsteady and quasi-steady simulations with experimental data

3.2 Model B
With seven blades forward and five blades aft,the fluctuations of total thrust and torque arising from forward and aft propeller interactions are of quite high frequency,i.e,fmin=70n when both propellers have the same rotation speed.Because the blade numbers of Model B are larger than those of Model A,the amplitudes of force fluctuations for Model B are expected to be smaller than those for Model A.On the other hand,the thrust and torque of each blade of either the forward or aft propeller should vary at twice the blade frequency of either the aft or forward propeller since each blade of one propeller encounters all blades of the other propeller twice in a complete revolution.Theoretically the force variations of adjacent blades of the same propeller should only have a phase difference of 2π/Z.
In Fig.5 an example is given of the computed thrust and torque variations for each blade at J=1.4.Mainly due to the differences in mesh distribution among different portions of the sub-domain A and E(see Fig.1),the computed thrust and torque variations for different blades of the same propeller do not repeat each other when shifted by 2π/Z.This is more obvious in thrust,as seen in Fig.5(a),though with this inaccuracy one can easily verify that the variation frequency is correctly computed.
Fig.6 shows the fluctuations of total thrust and torque at the same operating condition.Although the time step size which corresponds to 0.9° spatially is sufficient to resolve at least the lowest fluctuation frequency(fmin),it can be seen in Fig.6 that the inaccuracies revealed in Fig.5 make the total thrust and torque fluctuate in a noisy way.All the fluctuation amplitudes are less than 0.5% of the corresponding time-averages.


Tab.3 Comparison of the open-water performance of Model B obtained from unsteady simulations with experimental data
The time-averaged thrust and torque are shown in Tab.3 and Fig.7.The maximum error in predicted thrust is 6.4% for both forward and aft propellers,but in predicted torque it is up to 13.5% The open-water efficiency is under-predicted for the range of J computed,with a maximum error of 5%.

4 Concluding remarks
A CFD modeling approach has been presented in this work for predicting the unsteady performance of contra-rotating propellers operating in open water.To verify the approach two sets of CRPs are computed and compared with available experimental data.It is found that
(1)For special blade combination such as that of Model A,interactions between the forward and aft propeller blades are strong and of low frequency so that the unsteady modeling approach is essential to achieve high accuracy of prediction and,
(2)For practical blade combination such as that of Model B,the unsteady modeling approach is capable of predicting the open-water performance with reasonably good accuracy.However,to resolve the high frequency interaction between the forward and aft propellers,it is considered most important that the computational meshes are kept cyclic among the blades.Fortunately,the interaction becomes weaker as its frequency becomes higher,so that it can usually be ignored for practical blade combinations.
Although it is becoming increasingly common to apply CFD simulation in the study of marine propeller performances,simulating the unsteady performance of CRPs still presents a challenge to the hardware at least.To apply the unsteady modeling approach routinely in the design of CRPs,grid dependence,suitable turbulence model,as well as parameters of the computational model need to be further studied.
[1]Tsakonas S,Jacobs W R,Liao P.Prediction of steady and unsteady loads and hydrodynamic forces on counter-rotating propellers[J].Journal of Ship Research,1983,27(3):197-214.
[2]Yang C J,Tamashima M,Wang G Q,Yamazaki R.Prediction of the steady performance of contra-rotating propellers by lifting surface theory[J].Transactions of the West-Japan Society of Naval Architects,1991(82):17-31.
[3]Yang C J,Tamashima M,Wang G Q,Yamazaki R.Prediction of the unsteady performance of contra-rotating propellers by lifting surface theory[J].Transactions of the West-Japan Society of Naval Architects,1992(83):47-65.
[4]Liu X L,Tang D H,Hou Y.Prediction of steady performance of contra-rotating propellers by potential based panel method[J].Shipbuilding of China,2009,50(3):1-8.(in Chinese)
[5]Rhee S H,Joshi S.CFD validation for a marine propeller using an unstructured mesh based RANS method[C]//Proceedings of FEDSM’03,Hawaii,USA,2003:1157-1163.
[6]Cai R Q,Chen F M,Feng X M.Calculation and analysis of the open water performance of propeller by CFD software Fluent[J].Journal of Ship Mechanics,2006,10(5):41-48.(in Chinese)
[7]Liu Z H,Xiong Y,Ye J M,Tan T S.Study on the prediction of propeller open-water performance using RANS formula and multi-block hybrid meshes[J].Journal of Hydrodynamics,Ser.A,2007,22(4):450-456.(in Chinese)
[8]Zhang T,Yang C J,Song B W.Investigations on the numerical simulation method for the open-water performance of contra-rotating propellers based on the MRF model[J].Journal of Ship Mechanics,2010,14(8):847-853.(in Chinese)
[9]Newman J N.Marine hydrodynamics[M].The MIT Press,1999:85-88.
[10]Wilcox D C.Turbulence modeling for CFD[M].DCW Industries,Inc.,1994:83-95.
[11]Miller M L.Experimental determination of unsteady forces on contrarotating propellers in uniform flow[D].AD-A032 337,1976.
- 船舶力学的其它文章
- An Overview of Verification and Validation Methodology for CFD Simulation of Ship Hydrodynamics
- Numerical Calculation on the Influence of the Slot Size of Air Injection on Micro Bubbles Drag Reduction for Transitional Craft
- Application of Particle Swarm Optimization Theory in the Hydrofoil Design
- Application of Wavelet Denoising in the Modeling of Ship Manoeuvring Motion
- Local Wave Applied to Detect and Characterize Acoustic Emission Signals
- Vibration of Cracked Plates under Tensile or Compressive Load

