不同学科属性的被引次数之对应关系研究

●郭 强，赵 瑾，王玲玉，谭双岸，贾光耀，路世玲

（1.郑州大学 信息管理系，郑州 450001；2.中国人民解放军炮兵学院 军事运筹教研室，合肥 230031）

作者的h指数是建立在作者论文的被引次数的基础上，［1］由于不同的学科属性乃至同一学科的不同发展阶段会对文献被引次数之间的可比性造成影响，进而也会影响h指数的可比性，所以是否可以通过考察不同学科属性的被引次数之间的换算关系来探讨不同学科属性的h指数的对应情况，由此，对于被引次数的学科比例关系进行考察会具有一定的实际意义。

1 按布拉德福定律求不同学科的被引次数关系

对被引次数换算关系的初步考察希望能够建立在已知的分布规律的基础上。传统的布拉德福定律描述了在给定的考察时段内论文在所属期刊中的分布状况，对于特定的学科或主题，如果将期刊按照所包含的论文数量降序排列，并在此基础上对期刊进行分组，使得每组期刊分别对应于相同的论文累积量，则此时各个分组的期刊累积数量会构成等比数列，其中的公比为布拉德福常数。进一步地，对于被引次数而言，布拉德福定律是否同样具有其适用性，例如作者的被引次数在作者中是否也存在类似的布拉德福分布的特征，也即将作者按照其被引次数降序排列，并对作者进行分区，使得各个分区对应相同的累积被引频次，那么此时的各分区作者累积数是否也会形成等比数列；如果布拉德福定律对于作者的被引次数同样适用，那么能否利用作者被引次数所服从的这种分布规律来对不同学科的被引次数之间的关系进行大致的估计。

如果考虑学科的不同发展阶段以及数字与网络环境等因素的影响或是这些因素之间的相互作用，被引次数在作者中的分布在不同的情况下可能会具有不同的表现形式，从而针对特定作者集的被引次数所进行的分布考察，得到的结果可能会有其局限性。由于CNKI镜像站版将其入库期刊按照学科属性进行了分类，并且其引文数据库能够提供各期刊的作者被引排名列表，其中包括考察期刊的论文作者以及相应的被引次数，所以在这里将其作为数据来源，且数据统计时间为2010年1月。不失一般性，首先选取数学学科作为考察对象，在期刊分类表中的基础科学类内，归属于数学分类的期刊共计为53份，将这些期刊的所有论文作者作为对数学领域的作者集的近似，而作者的被引次数则可以通过这些期刊的作者被引排名来得到。在每份期刊的排名列表中，某作者的被引次数为该作者在该份期刊中所发表的所有论文的总的被引次数，如果某个作者同时出现于不同期刊的排名列表中，则将这些列表内与该作者对应的被引次数在作者查重后进行求和，在这里是利用被引排名列表中所给出的作者所属机构来对同名作者进行初步的查重，由此将所得到的和值作为对该作者的被引次数的近似。这种近似性首先是由于所采取的简化查重有其粗糙性，其次则是近似认为作者发表在其所属领域的专业期刊中的论文占该作者论文总量的主要部分，所以对于数学领域的作者在其他领域发表数学论文的情形，在这里并没有将相应的被引次数计算在内。同理，对于基础科学类下属的基础科学综合分类，作者在这些综合性期刊中所发表的论文以及相应的被引次数在这里也没有考虑在内。还需要指出，在这里类似得假设作者的论文被引次数占其总被引次数的主要部分，所以在此只是针对期刊论文来考察作者的被引次数，而作者的著作被引情况则没有纳入进来。

对于具有交叉学科属性的期刊，例如基础科学类所包含的非线性科学与系统科学类期刊，以及力学类中的相关计算类期刊，其中的论文作者与被引次数也没有纳入进来，其原因是由于从直观上，根据上述假设得到的作者与其被引次数能够大致反映数学领域的作者被引概况，同时，如何将交叉研究内容划归于数学领域也还需要做进一步的考察，实际上由于数学学科与其他学科领域之间的交叉关系，所以在这里针对该学科进行考察，学科边界所具有的模糊性使得对该学科的严格划分本身就具有其粗糙性。

如果能够认为以上的假设以及原始数据的确定从直观上具有一定的合理性，那么由此可以得到数学领域的作者与其被引次数的记录共计为35524项；如果将作者按照其被引次数降序排列，则有累积被引次数与累积作者数之间的关系如图1所示。

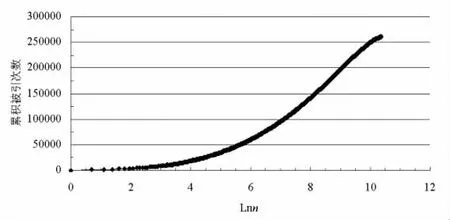
图1 数学学科的被引累积量与作者累积数的关系

在图1中，n为作者累积数，由此从直观上，被引次数在作者中的分布同样具有传统布拉德福分布的特征，而且也能够注意到在被引次数偏低的区域，被引累积量的增长率随作者累积数的增加所具有的下降情形。另外，按照传统布拉德福定律的分区描述，如果对作者进行分区，并且取分区数p为3，则能够得到此时的核心区作者数为922，相继分区的作者数比值的平均值为5.708，标准差达到0.716，而各分区的累积被引次数的平均值为88578，标准差仅为17.521。为了确定相应的布拉德福常数以及检验作者被引次数的分布是否服从传统的分区描述，需要考察引起相继比值的标准差偏高的因素，为此可以改变分区数。例如分别取p为5与7时，类似地可得相继分区的作者数的比值分别为3.540,2.487,2.323,3.896以及2.858,2.145,1.874,1.799,1.960,3.152，均值与标准差分别为3.062与0.775以及2.298与0.568，能够注意到居中处的相继比值的变化相对较为平稳，而在被引次数偏高或者是偏低的区域，特别是在起始及末尾分区处，作者数的相继比值会显著地高于居中处，从而可能会形成偏高的标准差。同时，如果改变分区数p为其他的取值，则从直观上也能够有类似的情形。由于作者是按照其被引次数降序排列，并且各分区具有相同的累积被引量，所以被引次数偏低处的相继比的异常说明了该区域作者具有显著偏低的被引次数，以至于被引累积量的增长率会出现下降的情形，由此末尾分区处偏高的相继比可能与格鲁斯下垂有关，而对于被引次数偏高处的比值异常，则可能是由于被引次数在作者中的分布相对较为集中，所以起始分区中的作者被引次数会显著偏高，该区域的作者数也会显著减少以满足该分区具有与其余分区相同的累积被引次数。因此该分区与其后续分区的作者数相继比也会显著偏高，毕竟与其他的评价指标例如下载次数相比，被引次数概念自身就具有相对较强的集中性，而且网络环境下文献获取的便捷性也能够造成下载次数的分散性。另一方面，在分布范围上，与期刊相比，期刊中的文献作者的针对性会更强，由此从直观上被引次数在作者中的分布会更为集中。那么，如果继续增大分区数p的取值，则有可能减少所得各个分区的累积量的波动幅度，从而在一定程度上减弱由格鲁斯下垂以及分布集中性所造成相继比异常。例如选取分区数p为13，可得相继分区的作者数比值分别为2.048, 1.736, 1.571, 1.486, 1.432, 1.382, 1.374,1.363,1.411,1.485,1.650,2.326，且均值与标准差分别为1.605以及0.301，或者说当分区数p足够大时，能够近似认为被引次数在作者中的分布服从布拉德福定律的传统分区描述，而且此时的布拉德福常数取为上述相继比的平均值。以上经验考察从直观上具有一定的合理性，与已有的研究结果也相吻合。［2］

还可以对被引次数与作者数之间的关系进行曲线拟合，［2］能够得到累积量之间的分段拟合函数为c=1680.1a0.5923与 c=51635Ln（a）-268067，其中 a 与 c 分别为作者累积数以及累积被引次数，且核心区与非核心区的决定系数分别为0.9858以及0.9957，由此被引次数在作者中的分布也服从布鲁克斯公式。

对于数学学科而言，上述讨论能够反映被引次数在作者中同样具有较为显著的布拉德福分布特征，进一步地可以改变学科属性。例如根据类似的假设以及原始数据的确定过程，能够得到生物领域的作者与其被引次数的记录共计为133858项，如果将作者按照其被引次数降序排列，则在此基础上，该领域的累积被引次数与作者累积数之间满足与数学学科相类似的图像及分区描述，而且曲线拟合的结果与布鲁克斯公式也相吻合。

如果这种布拉德福分布对于不同的学科属性具有一般性，则可以尝试对不同学科的被引次数之间的关系进行初步的确定。假设有两不同学科1与2，分别对该两领域的作者进行分区，且取分区数p为3，并设所得到的核心区的作者数分别为r1与r2，各分区对应的累积被引次数分别为p1与p2，以及此时的布拉德福常数分别为k1与k2。如果学科属性1中的一次被引相当于学科属性2中的x次，那么将此关系代入到学科1中，则应当保证此时学科属性1中的分散程度与学科属性2相同，于是有学科属性1的布拉德福常数为k2，而核心区的作者数量可以发生变化，设为r2′，相应地有核心区对应的累积被引次数为xp1。由于 r2′+r2′k2+r2′k22=r1+r1k1+r1k12为学科 1 的作者总人数，所以当该总人数与k2均为已知时，则能够求得r2′，进而能够在学科属性2的按被引次数降序排列的作者列表中近似得到与作者累积数r2′对应的累积被引次数 xp1=（r2′/r2）p2，当 r2′,r2,p2,p1均为已知时，则能够求得x，由此对不同学科属性的被引次数之间的关系进行大致的估计。

以数学及生物学科为例，取分区数p为3，由以上讨论可知数学学科的核心区作者数为r1=922，累积被引次数p1=88578，以及此时的布拉德福常数为k1=5.708，对于生物领域，则类似地能够得到r2=3139，p2=601921，以及 k2=6.151。由于 r2′+r2′k2+r2′k22=35524，所以近似有r2′=790，那么与作者累积数r2′相对应的累积被引次数为 xp1=151487，从而有x近似等于1.710。可以对这种估计的互逆性进行考察，也即选取生物与数学领域分别作为学科属性1与2，此时有r1,p1,k1与r2,p2,k2分别为3139,601921,6.151以及922,88578,5.708。由于 r2′+r2′k2+r2′k22=133858，所以 r2′=3407， 那 么 与 r2′对 应 的 累 积 被 引 次 数xp1=327315，于是此时的x近似为0.544，与学科属性互换前的x值的倒数也较为接近，偏差为7.01%。

另外，由于当分区数p足够大时，被引次数在作者中所具有的布拉德福分布特征会更为显著，所以进一步地可以选取p为较大值。例如当p等于5时，数学与生物学科的作者数分别为r1=313与r2=1071，相应的累积被引次数为p1=53147以及p2=361153，而布拉德福常数则为k1=3.062以及k2=3.214，类似地有r2′+r2′k2+…+r2′k24=35524，于是 r2′=230，则与该 r2′对应的累积被引次数为xp1=77559，所以x近似为1.459。需要指出，在利用等式 r2′+r2′k2+…+r2′k2p-1=A1对 r2′进行确定的过程中，随着分区数的逐渐增加，所得到的r2′对于k2的取值也会更为敏感，但是起始及末尾分区处作者数相继比异常的客观存在，使得需要考察此处的布拉德福常数k2的确定，其中A1为学科属性1的作者总数。当分区数较小时，各分区作者数的相继比具有偏高的标准差，从而会影响上述建立在布拉德福分布基础上的估计过程的合理性，而当选取较大的分区数时，由于此时相继比的标准差相对较小，从而取作者数相继比的平均值来作为对布拉德福常数的一种较好的近似，但是在这里r2′对于k2的高度敏感性使得这种近似有时也会对r2′带来较大的偏差，从而可能会引起估计结果的失真。例如选取分区数p为13，则此时对于数学及生物学科分别有作者数为r1=63以及r2=182，对应的累积被引次数为p1=20441与p2=138905，以及此时的布拉德福常数分别为k1=1.605与 k2=1.691， 类 似 地 可 以 有 r2′+ r2′k2+ … +r2′k212=35524，于是有 r2′近似为27，从而与r2′对应的累积被引次数为xp1=20607，则x近似等于1.01，而这种被引次数之间的近似等效从直观上与实际情况并不相符，毕竟数学与生物领域之间的学科差异，以及研究人员的总量与科研产出的规模的不同，都会使得单次被引所表征的作者文献的学术价值有所不同，而形成这种估计结果的原因则是由于其中的布拉德福常数都是利用相继比的平均值来得到。实际上可以将所得k1与k2分别带入ri+riki+…+riki12=Ai进行检验，其中i=1,2，Ai为学科属性i的作者总人数，则有A1=48734以及A2=243215，相对于原始数据，偏差分别达到了37.2%以及81.7%，所以由此得到的r2′与x也会与实际情况不相吻合。作为对照，还可以考察分区数较小时的情形。例如当p等于3时，按照由相继比平均值得到的k1=5.708与k2=6.151，类似地有A1=36225以及A2=141210，此时与实际数据的偏差分别仅为1.97%以及5.49%。

另一种对布拉德福常数的近似则是不考虑作者数相继比异常的区域，从而能够保证剩余区域的相继比具有相对较小的波动，由此取其平均值来对布拉德福常数进行确定，但是所忽略的相继比异常往往会与变量自身的分布特性有关。例如上文中作者被引次数的格鲁斯下垂及其集中分布特性，所以由此得到的布拉德福常数是否全面，如果具有全面性，也即仅仅是居中分区处的分布服从传统的布拉德福分布，那么是否能够只利用居中区域来进行类似的被引次数相互关系的估计，这些还需要做进一步的考察。例如当p等于13时，除去起始与末尾分区，数学与生物学科的作者数为r1=129以及r2=460，累积被引次数仍然取p1=20441与p2=138905，而布拉德福常数则为k1=1.489与 k2=1.480，由 r2′+r2′k2+…+r2′k212=19870 可得 r2′近似等于59，其中19870为数学学科剩余分区的作者总数，那么与r2′对应的累积被引次数为xp1=17728，所以有x近似等于0.867，从直观上该比例关系也与实际情况不相符合，毕竟在原始数据集中，与生物领域相比，数学学科的作者总数以及被引总量都相对较小，所以不严格地，如果可以认为该两领域的总的学术价值近似相同，则数学领域的单次引用会对应于更多的学术价值。

上述两种对布拉德福常数的估计都利用了作者数的相继比，而相继比的得到则是建立在原始数据的基础上，所以能否不直接由原始数据来对布拉德福常数进行确定，假定被引次数在作者中服从布拉德福分布，当然根据上文中的分布考察能够认为这种假定具有一定的合理性。那么仍然考察数学及生物学科，选取分区数p等于13，同样有作者数分别为r1=63以及r2=182，对应的被引累积量分别为p1=20441与p2=138905，由于 r1+r1k1+…+r1k112=35524且 r2+r2k2+…+r2k212=133858，其中等式的右边分别为数学及生物学科的作者总人数，所以将r1与r2代入后能够得到k1=1.557与k2=1.597，由于 r2′+r2′k2+…+r2′k212=35524，所以有 r2′近似等于48，那么与该r2′对应的累积被引次数为 xp1=36634，于是x近似等于1.792。由此得到的布拉德福常数能够避免由相继比的平均值来进行近似可能会带来的偏差，但是这种估计实际上是该常数的理想值，毕竟在起始及末尾分区处存在着显著偏高的作者数相继比。

2 被引次数比例关系的初步应用

利用被引次数之间的比例关系，能够对不同学科属性的h指数的对应关系进行大致的考察。例如作者1与2分别归属于数学及生物学领域，由h指数的定义，将该两作者的论文分别按其被引次数降序排列，并设所得列表分别为A={a1,a2,…,an}以及B={b1,b2,…,bm}，其中ai与bj分别为与序号i与j对应的论文的被引次数，如果认为数学学科中的单次被引相当于生物学科中的x=1.792次，则有列表A变换为{xa1,xa2,…,xan}，由此能够求得相应的h指数并记为h1′，而h1′与h2则具有一定的可比性，从而可以对不同领域的作者进行比较，其中h2为作者2的h指数，并记h1为作者1在被引次数变换前的h指数。例如设A={10,6,4,4,3,2,2,1}以及 B={19,11,11,8,8,6,6,5,4,3,3,3,3}，则相应地有h1=4以及h2=6，而变换后的列表A近似等于{18,11,7,7,5,4,4,2}，则有h1′=5，那么此时能够认为与作者2相比，作者1的h指数相对较小。

或者说是对数学学科中某作者的h指数在生物领域中的对应值做近似的估计。例如取作者1的论文被引次数列表为{37,21,15,14,7,6,4,3,3,3,2,2,2}，那么有h1=6，将被引次数按照比例关系1.792换算到生物学科，相应地有被引次数列表近似为{66,38,27,25,13,11,7,5,5,5,4,4,4}，以及此时的h指数为h1′=7。由于上述对x的估计满足学科互逆性，所以对于此处的h指数的换算过程，互逆性同样能够得到保持。

另外，从直观上能够注意到在作者的论文列表中，作者论文的被引次数通常会具有显著偏高的递减速率，特别是在序号偏低处，而随着论文序号的增加，被引次数的递减速率也会逐渐降低，由此在这里假设论文的被引次数与论文的序号之间近似服从负指数关系，那么进一步地可以假设作者1的论文被引次数满足等式c=t1exp（-t2s）+t3；其中c与s分别为论文的被引次数及序号，且t1,t2,t3均为待定常数，那么此时会有h1满足h1=t1exp（-t2h1）+t3，如果将数学学科的被引次数按上文中的比例关系换算到生物学科中，则应有 c′/x=t1exp（-t2s）+t3，即 c′=xt1exp（-t2s）+xt3，其中的c′为换算后的论文被引次数，那么作者1在此时的 h 指数应满足 h1′=xt1exp（-t2h1′）+xt3，将该方程与 h1所满足的等式联立，则能够得到h1,h1′与参数t1,t2,t3之间的关系，而后者与该作者的被引次数的分布相对应。例如仍取作者1的论文及被引次数列表为{37,21,15,14,7,6,4,3,3,3,2,2,2}，则有拟合函数为c=53.252exp（-0.453s）+2.033，且决定系数为0.984，由此应当有 h1′=53.252xexp（-0.453h1′）+2.033x；如果取x等于1.792，则会有h1′=7.238，这与直接从实际被引次数分布中得到的h1′=7也较为接近。

进一步地，在h1与x为已知的情况下，是否可以不需要对论文被引次数的分布进行具体的统计，仅利用这种负指数关系来对作者h指数的换算关系做近似的估计。例如在这里假设作者1的论文被引次数与论文序号之间的关系为c=texp（-ts），其中t为待定正常数，变量c与s的含义同上，那么类似地会有h1=texp（-th1），且换算后的论文被引次数与作者的h指数分别满足 c′=xtexp（-ts） 以及 h1′=xtexp（-th1′），由此当 h1与x为已知时，t与h1′的取值也可以确定下来，所以在这个角度上，能够得到将数学领域的某作者的h指数换算到生物学科的换算关系，同时需要指出，采取这种形式的负指数关系是为了减少待定常数的个数，以便能够对换算关系进行确定，但是其精度可能会有所下降，毕竟这种函数形式并非是被引次数与文献序号之间关系的最佳拟合，而且这种拟合函数所具有的偏差可能还会引起参数t以及h1′的无法确定。例如仍取被引次数列表为{37,21,15,14,7,6,4,3,3,3,2,2,2}，相应地h1等于6，由于Ln（t）-6t-Ln（6）＜0，所以有texp（-6t）＜6，所以当h1取6时方程h1=texp（-th1）无解。因此对于特定作者而言，仅利用h1与x来对h1′进行估计，尤其是得到公式化的近似关系，还需要做进一步的探讨。

还需要指出，以上确定比例关系x的过程是建立在两个学科的所有作者的基础上，所以应用于个体时会存在偏差，因此希望能够得到归属于不同学科的作者的h指数在整体上的对应关系。与上述对个体作者的考察类似，可以从原始数据出发对所有作者h指数的换算结果采取某种形式的平均，或者是利用论文被引次数与其序号之间的关系等，来得到整体上的换算关系，从而可以利用所得到的大致比例，对某学科作者的h指数相当于另一学科多大的指数值来进行判断。

除了对不同学科属性的h指数进行考察之外，还可以对建立在论文被引次数基础上的其他综合指标进行类似的学科比较，例如往往会有这样的情形，某期刊在其所属领域与其他学科的另一期刊具有同样的学术价值或者是影响力，但是两者的影响因子却具有较为显著的差异，由此是否能够对不同学科的期刊影响因子进行比较或是换算，从而可以更好地应用影响因子来对期刊进行统一的衡量。类似地，可以利用不同学科中被引次数的比例关系来对期刊影响因子的学科对应情况进行考察，并取数学及生物领域的期刊作为考察对象。由于CNKI镜像站版的引文数据库能够给出其入库期刊的逐年被引量以及文献间的引用关系，所以可以得到在考察年度内某数学期刊的被引文献的年代分布。那么按照期刊影响因子的定义，根据发表时间为考察年度前两年的期刊文献在考察年度的被引次数，以及该期刊在考察年度前两年的载文量，能够得到该数学期刊在考察年度的影响因子，如果将数学期刊的被引次数按照比例关系x换算到生物领域，并且不考虑论文数量可能也存在着的对应关系，则有变换后的期刊影响因子为变换前的x倍。例如由CNKI镜像站版给出的期刊分类表，能够得到数学分类中各个期刊的影响因子的平均值近似等于0.377，如果取x为1.792，则变换后的平均值应为0.377x=0.676，类似地可以有生物分类中期刊影响因子的平均值为0.730，与数学期刊变换后的影响因子平均值相比，偏差为7.96%；如果可以认为数学与生物领域从整体上会具有近似相同的学术价值或是学术影响力，则这种较小的偏差能够从侧面反映所得到的x值具有一定的合理性，其中期刊影响因子的统计时间为2010年1月。

但是需要指出，因为不同学科的发展过程会存在差异，所以不同时期的被引次数比例关系从直观上也会有所不同，由于在上述确定x的过程中并没有考虑时间因素，所以在此得到的影响因子对应关系与某实际考察年度的对应情况之间应当会存在偏差，那么对于被引次数比例关系的确定，进一步地可以通过被引次数在期刊中的布拉德福分布做类似的确定，一方面可以将确定过程以及所得结果与在作者中的分布考察进行对比及检验，以便做进一步的修正；另一方面可以确定时间段来考察被引次数在作者或者是期刊中的分布状况，从而得到x在不同考察时段的取值乃至随时间的变化情况。

除此之外，还可以通过变换考察对象来对被引次数的比例关系进行估计，根据核心与非核心期刊的论文之间的相互引用所得到的x值，对于其他的考察对象可能并不完全适用，毕竟作者与被引次数的统计范围会有所不同，而且对于不同的考察对象，不同学科属性的被引次数之间的换算关系可能也会存在实质上的差异，由此可以用来对所得到的比例关系进行检验以及修正。

3 结束语

应当说上文中对x取值的估计较为粗糙，例如分区数p取为13具有随意性，而且是在作者数的相继比在首尾分区处明显偏高的情况下将布拉德福常数取为其理想情况，所以在这里只是希望能够对不同学科属性的被引次数进行大致的比较，并对相关综合指标的学科比例关系的确定进行初步的尝试，其基本的假设是在被引次数进行变换后会具有相同或者是相似的效果。另外，除了布拉德福分布规律，对于被引次数的比例关系的进一步考察还可以建立在其他规律诸如某种形式的洛特卡分布的基础上，最终的目的是希望提高所得结果的置信度以及具有较好的实用性。

［1］ JEHirsch.Anindextoquantifyanindividual’sscientific researchoutput［J］．PNAS，2005，102（46）：16569－16572.

［2］张洋.期刊Web下载总频次的布拉德福分布研究［J］．图书情报知识，2006 （6）：38－42，60.