振动环境中相机位置坐标与姿态角解算的实验研究

张征宇,罗 川,孙 岩,周桂宇,黄诗捷

(1.中国空气动力研究与发展中心 空气动力学国家重点实验室,四川 绵阳 621000;2.西南科技大学信息工程学院,四川绵阳 621000)

0 引 言

风洞试验是飞行器气动布局设计不可缺少的环节。为了提高试验数据的精、准度,需获取模型变形测量数据。国外有的风洞(如欧洲的DNW、NLR)即使在模型变形量未超过试验规范要求时,依然测量模型变形,修正试验数据以提高试验数据精度[1-3]。

美国从20世纪80年代开始研究模型变形视频测量(VMD)技术[1-4],现已应用于各种低速、高速、超高速风洞模型的运动轨迹、变形和姿态角的测量[3-4]。

国内高速暂冲式风洞振动较欧美连续式风洞大,导致VMD相机的位置与姿态随着洞体振动而动态变化大。因此,从描述相机、像点、模型待测点三点数学关系的共线方程可知：从VMD的相片信息中准确确定相机位置与姿态角,对于振动环境中实现VMD测量至关重要[3-4]。

目前,相机位置坐标与姿态角求解主要有3种方法：基于直接线性变换(DLT)的解法、角锥法、光束平差解法[5-7]。其中,DLT因至少需要6个非共面控点,其实用性受到限制;角锥法主要用于为光束平差解法提供迭代计算的初值,计算精度没有光束平差解法高。

为此,通过搭建的实验平台,研究角锥法、光束平差解法和空气动力学国家重点实验室建立的基于蒙特-卡洛法[8]的相机位置坐标与姿态角求解法,比较其在风洞试验振动模拟环境中的解算效果,以建立适应我国风洞模型变形测量的相机位置坐标与姿态角解算方法。

1 风洞试验的振动模拟实验平台设计

实验目的：在风洞试验的振动环境下,研究不同的相机位置坐标与姿态角解算方法的效果与稳定性,确定最适于VMD采用的相机位置坐标与姿态角解算技术。

实验平台采用的硬件如下：labworksR○的激振器2个(包括ET-126B-4规格的执行器2个,Pa-141规格的功率放大器2个)、DALSAR○相机2个(分辨率为400万像素,成像幅面为17.4mm×12.8mm)、图像采集电脑2台、35mm定焦镜头2个、目标靶面一个以及编码标记点,具体参见图1。

图1 风洞试验振动环境模拟实验平台Fig.1 Experimental platform for simulating wind tunnel vibration

2.4 m跨声速风洞试验时的低频振动峰值频率在7Hz左右,因此,首先进行给定振幅为8mm、频率为7Hz的正弦振动环境实验,再进行振动频率不超过10Hz的随机振动环境实验,相机曝光时间为5ms,以模拟双相机在风洞试验中的测量环境。

2 实验研究的方案

2.1 测量原理

描述相机、目标靶面上编码点及其像点三者关系的共线方程表达式如下：

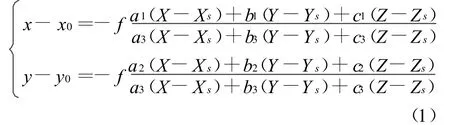
式中(x0,y0)分别为相机像平面中心,f为相机焦距, ()分别为相机在地面坐标系下的位置坐标, ()为相机姿态角(φ,w,k)所组成的旋转矩阵R中的9个方向余弦,(x,y)与(X,Y,Z)分别为目标靶面上编码点的像平面坐标与地面坐标系下的坐标。

因此,当已知3个以上的目标靶面上编码点坐标,即可通过式(1)解得相机位置与姿态角参数。

2.2 实验方案

(1)用三个控制点的角锥法[5-7]求得初值,分别代入基于蒙特-卡洛法的相机位置坐标与姿态角求解法和光束平差解法[5-7],其中基于蒙特-卡洛法的相机位置坐标与姿态角求解法,是指采用解非线性方程的蒙特-卡洛法[8],求解式(1)得到相机位置与姿态角参数;

(2)用未振动时相机的安装位置与姿态角作初值,分别代入基于蒙特-卡洛法的相机位置坐标与姿态角求解法和光束平差解法;

研究采用传统的6参数畸变[9-10]模型进行相机畸变校正,采用的相对误差计算式为：

3 实验数据与结果分析

正弦激振下左相机像片的相机位置坐标与姿态角解算结果的误差如图2所示,随机振动下右相机像片的相机位置坐标与姿态角解算结果数据如表1所示,因激振频率设定值低于10Hz,故表1与图2中仅列出能够描述一激振周期的10张照片,表中A-D的具体含义如下：

(A)表示三控制点的角锥法求解结果;

(B)表示将角锥法结果作为初值代入光束平差算法解得的数据;

(C)表示将角锥法结果作为初值代入基于蒙特-卡洛法的相机位置坐标与姿态角求解法解算的数据;

(D)表示将相机未振动时的位置参数作为初值代入光束平差算法所得的数据,其中左相机坐标为(-407.3525,-165.1383,1873.696),姿态角为(0.2150157,0.1209951,-0.130937);右相机坐标为(-289.3503,80.00066,1984.518),姿态角为(0. 163873,-0.05584956,-0.1130597)。

图2与表1中的测量实验结果表明：

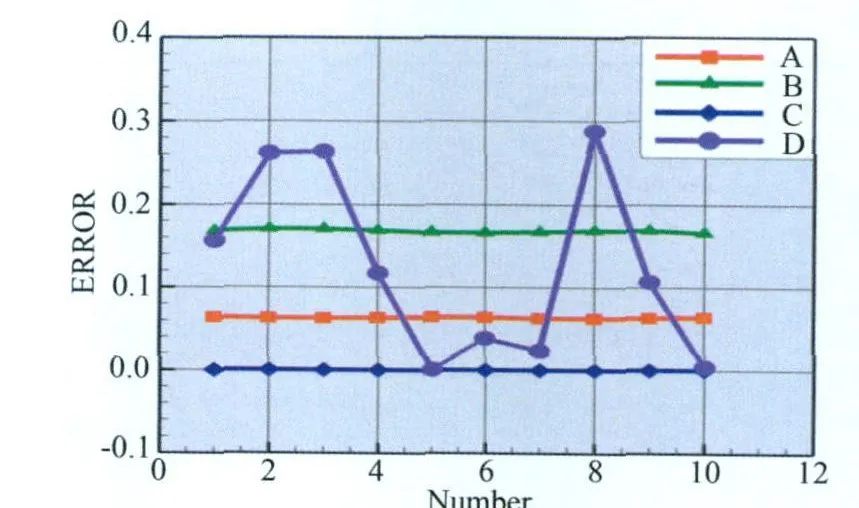
图2 正弦振动下左相机的位置与姿态参数解算误差Fig.2 Errors of left camera orientation in sine vibration

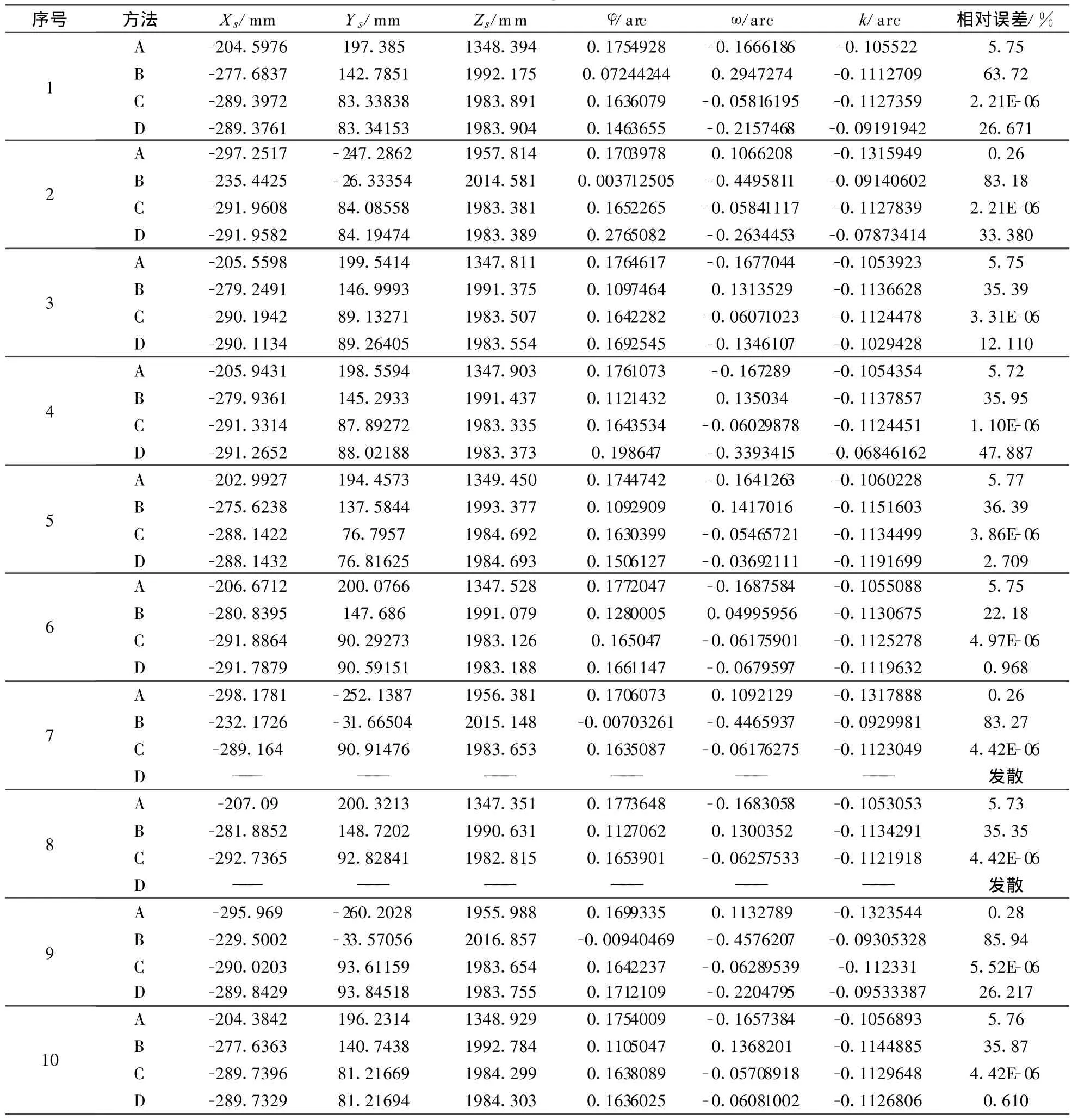
表1 随机振动下右相机的位置与姿态参数解算数据Tabel 1 Exterior orientation of right camera in random vibration

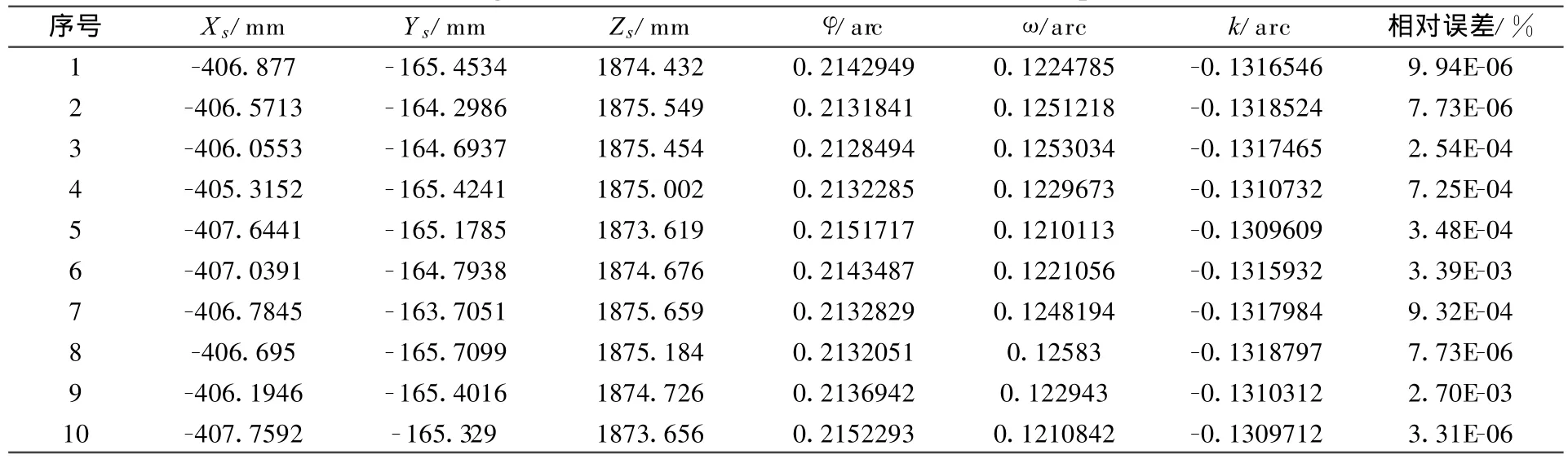
表2 使用蒙特-卡洛解算结果为初值的光束法解算数据表(左相机正弦振动)Tabel 2 Exterior orientation using bundle method with Monte-Carlo solution input(left camera in sine vibration)

(1)角锥法在两种振动状态下均能得到结果,但其相对误差在6%左右。

(2)基于蒙特-卡洛法的相机位置坐标与姿态角求解法在以角锥法结果和相机初始位置为初值时均能收敛至正确的相机位置坐标与姿态角,实验中最大的误差为6.62E-8,求解稳定性最好。

(3)光束平差法在以角锥法所得结果为初值下收敛效果较差,由图2和表1可以看出,由于角锥法初值相对误差较大,代入光束平差法难以收敛至正确解;将相机初始位置与姿态值代入光束平差法,仅在某些时刻能收敛于正确解,如图2序号1(此时未振动)、序号6和序号11,表1序号1(此时未振动)、序号11。

光束平差法对初值精度依赖较高的原因是：其采用数值计算理论中解非线性方程组的Newton法求解,即通过泰勒展开取一次项线化方程,然后求解改正数逐步迭代求解,当在真实解附近泰勒展开时,因二次及高阶小项较小,线化时截断误差较小,此时能迭代收敛至正确解;若初始值偏离真实值太远,舍去二次及高阶小项后,线化时截断误差较大,导致光束平差法不收敛或收敛至局部最优解,这与数值计算方法的基本理论吻合：“当初值不够准确时,New ton方法往往得不到正确解”。

角锥体法也采用数值计算理论中解非线性方程组的Newton法求解,当相机位置坐标的初值不准确时,同样也导致迭代不收敛或收敛至局部最优解,导致其相对误差较大(在6%左右)。

为验证以上分析,如表2所示,将蒙特-卡洛法的相机位置坐标与姿态角求解结果代入光束平差算法,发现光束平差算法就能收敛到正确解(最大相对误差3.39E-5);另一方面也验证了基于蒙特-卡洛法的相机位置坐标与姿态角求解法的正确性。

如图3所示,基于20张时序照片(即20次时序测量)的相机与支杆一起振动轨迹反映了正弦激振规律,其振动频率在7Hz左右,由于支杆刚性的影响(如图1所示本次实验采用相机支杆较长较细),所以在x轴与y轴方向有晃动,由于设定振动在z轴方向,故z轴方向受支杆刚性影响较小,所以能明显看出其周期性,而在 x轴与y轴方向相机位移的周期性不明显,但是x轴最大位移与y轴方向基本相同;如图4所示,在7Hz的正弦激振下,相机姿态角的变化基本符合正弦变化规律。如图5与6所示,相机与支杆一起振动轨迹无规律,其轨迹响应符合设定的随机激振方式。上述分析表明基于蒙特-卡洛法的相机位置坐标与姿态角求解法结果与振动设定的激励方式相符。

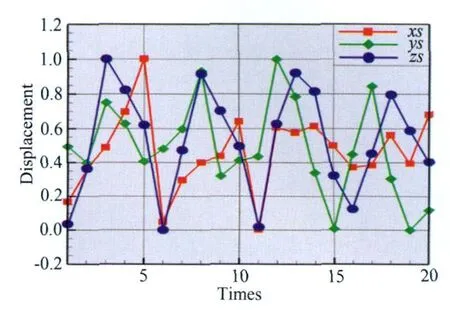
图3 正弦激振下左相机位置的当量位移图Fig.3 Normalized displacements of left camera in sine excitation

图4 正弦激振下左相机姿态角的当量角位移图Fig.4 Normalized angular displacements of left camera in sine excitation

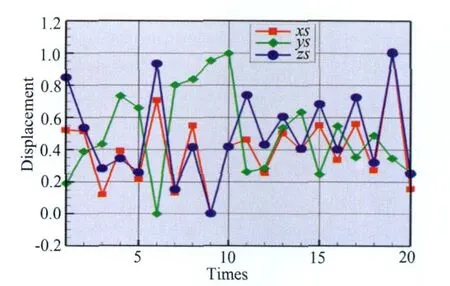
图5 随机激振下左相机位置的当量位移图Fig.5 Normalized displacements of left camera in random excitation

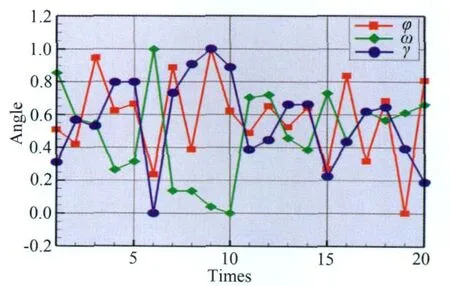
图6 随机激振下左相机姿态角的当量角位移图Fig.6 Normalized angular displacements of left camera in random excitation

4 结 论

建立了高速风洞的振动模拟地面实验平台,对比4种相机位置与姿态角求解效果,发现：

①光束平差法对初始值精度依赖性较强,难以在振动环境的VMD测量中推广;

②基于蒙特-卡洛法的相机位置与姿态角求解法对初始值精度依赖性最弱,求解稳定性最好,在振动环境中初始值相对误差达到6.387%,其求解结果的相对误差仍然保持在6.62E-8以内,最适于振动环境中VMD测量的相机位置与姿态角求解。

致谢：该研究得到中国空气动力研究与发展中心高速所的大力支持,在此表示衷心感谢!

[1] LE SANT Y,MIGNOSI A,DELÉGLISE B.Model deformation measurement(MDM)at Onera[R].AIAA 2007-3817.

[2] LIU T,BURNER A W,PAPPA R.Photogrammetric techniques for aerospace applications[R].AIAA 2008.

[3] DANNY A BARROWS.Videogrammetric model deformation measurement technique for wind tunnel applications [R].AIAA 2007-1163.

[4] LE Sant Y,MERIENNE M C,LYONNET M.A model deformation measurement method and its application on PSP measurements[R].AIAA 2004-2192.

[5] 冯文灏.近景摄影测量-物体外形与运动状态的摄影法测定[M].武汉：武汉大学出版社,2002.

[6] 黄桂平,叶声华,李广云.数字近景工业摄影测量关键技术研究与应用[D].[博士学位论文].天津大学, 2005.

[7] 邾继贵,叶声华.基于近景数字摄影的坐标精密测量关键技术研究[J].计量学报,2005(7)：207-211.

[8] 金 畅,夏尊铨.蒙特-卡洛方法中随机数发生器和随机抽样方法的研究[D].[硕士学位论文].大连理工大学,2005(12)：1-5.

[9] 武汉大学测绘学院.误差理论与测量平差基础[M].武汉：武汉大学出版社,2005.

[10]梁 晋,肖振中,唐正宗,等.大型飞机风洞变形测量的相机标定研究[J].西安交通大学学报,2009,(43)：55-59.