测量叶轮机振动叶片表面非定常气动响应的实验技术 影响系数法

杨 慧,郑 赟

(北京航空航天大学航空发动机数值仿真研究中心,北京 100191)

0 引 言

自1945年Shannon[1]报道了第一起叶轮机叶片气动弹性失效故障以来,与非定常流动耦合的振动问题就成为设计者关注的传统难题。叶片颤振为自激振动类气动弹性稳定性问题。在计算和分析能力不足的初期,借鉴以往机翼失速颤振的经验,通过在高速旋转机械上实施的自由颤振试验,确定颤振发生时的气动条件,组建统计数据库,获得一些经验公式或半经验公式,以此作为“设计准则”,预测和避免现有机型发生颤振。但经验法不足以用来理解叶轮机内部真实流动的非定常特性,例如三维效应和粘性效应对非定常流动特性的影响。这种经验预测方法还会造成过保守的设计而牺牲了发动机性能,或者会导致大规模的重新设计而增加研制成本。例如带冠叶片和带凸台叶片不但增加了重量而且提高了结构动力特性分析的不确定程度。目前叶轮机高推重比的设计追求导致更高的级负荷,更轻的结构和更紧凑的级间距,这些趋势都造成气动弹性问题在新机型上越来越突出,但颤振发生的气动条件并不在经验数据库中,因此,经验法无法应用于新机型。

现已知振动叶片表面的非定常气动响应为颤振的驱动机制,随着计算技术、算法和计算硬件的发展,计算流体动力学(CFD)成为预测振动叶片表面非定常负荷的有用工具。常规的叶轮机定常气动设计只关注一个或二个工作点,而气动弹性分析没有清晰的参考点,需要检验一系列的气动工作条件,每种工况又要计算所有叶片间相位角下的气动阻尼,才可以确定气动弹性最不稳定工况。针对每一个非定常考核点,如果使用全三维粘性非定常时间推进法,由于时间步长受最小网格尺寸的限制,加上计算域为多通道甚至全环,一种叶片结构的气动弹性分析就需要几周到几个月的工作量。为了提高计算效率,发展了时间线性化方法[2-3],假设叶片的振动是叠加在定常流上的小扰动。但是这一假设对流体和振动叶片耦合性很强,以及叶片运动形式不可知的情况,是不适用的。为了解除这一约束,根据所研究问题的侧重点,又发展了时间推进的欧拉法[4],薄层雷诺平均Navier-Stokes(N-S)法[5],以及雷诺平均的N-S法[6]。方程越复杂,数值模拟的精度越高,但求解时间越长,为了解决这一矛盾,研究者们使用了不同的空间和时间离散方法、复杂程度不同的湍流模型、以及单通道计算域。而这些近似程度不同的数值模型的有效性需要试验数据的验证,不同模型的适用范围以及局限性必须建立。由于缺乏合适的实验验证数据,只能新旧模型之间互相检验。这种状况对建立理论模型的有效性,发现已有模型需要改进的地方,以及指出新模型的发展方向都是不利的。

随着测量技术的发展,试验研究的目的由识别宏观颤振边界转向探讨颤振发生的微观物理机制。气动弹性试验也由传统的整机或部件试验转向为校核数值模拟方法服务的基础实验。同时还具有另外二个重要目的：(一)以考察影响参数的方式,深入理解与振动绕流相关的非定常流动的物理机制,为新的非定常气动模型提供理论基础;(二)作为验证新概念,新方法,新思维的物理平台。目前与叶轮机气动弹性相关的基础性实验,国外已有很大发展,其中比较著名的有瑞典皇家工学院Bölcs&Fransson[7]汇编的叶轮机气动弹性标准算例集及其团队后续的实验工作,研究者们在美国NASA Lewis跨声速振荡叶栅台上的实验[8-9],以及英国He进行的一系列基础气动弹性实验[10-12]等。而国内,这方面还没有起步。相关验证实验数据的缺乏,以及与国外资源非共享的局面,阻碍了国内叶轮机气动弹性自开发程序代码的校核、发展与工程应用。本文介绍的气动弹性实验技术,可以弥补国内在这方面的欠缺。

叶片气动弹性实验分两类：自由颤振和可控振动。如上所述自由颤振试验多用于获取定型机的颤振边界,为校核程序提供叶片表面详细的非定常气动响应的不多。原因在于实施此类试验相当困难。驱动设备所需的能源很大[13];叶片表面的测点有限,通常只取一个横截面[14-16];高速流下测量数据的精度比较低;测量元件往往选择内置式的,安装困难,易损耗,标定工作繁琐;高频压力传感器引线困难,并受到数据采集系统的局限等等。由于商业敏感性的缘故,发表的自由颤振试验数据更少。这类试验数据,适用于程序代码的最终校核,但无法指出数值模拟方法中需要改进的地方。

与机翼不同,叶片级中相邻叶片存在互相的气动干涉,Lane[17]由行波理论定义的叶片间相位角σ是叶盘振动节径的表征量,也是描述振动叶片间气动耦合的重要参数。在非旋转叶栅(包括环形和线性叶栅)以行波理论为基础实施的可控振动模型,由于可以进行影响参数分析,被广泛应用于校核程序代码。传统上这些实验是以协调叶栅模型[18-20]进行的(所有的叶片以相同的频率、相同的振幅和一定的叶片间相位角振动)。通过测量叶片表面的非定常压力获得振荡叶栅的气动阻尼,气动阻尼是判断结构气动弹性稳定性的参数,也是影响强迫响应中振动应力量值的重要参数。实践中,对于现实的折合频率,控制所有的叶片精确地以相同的振幅和叶片间相位角振动是很困难的[21],需要很复杂的叶片驱振系统。对于协调叶栅实验,不仅要对所关注的定常流和折合频率范围作实验,还要针对每种情况遍取整个叶片间相位角范围,实验量非常繁重。另外,无法评估每个叶片对协调叶栅非定常气动响应的相对作用[22]。

影响系数法[23]是简化这一难题的有效途径,通过只振动一个叶片获得协调叶栅所有叶片间相位角下的非定常气动响应数据[24-26]。下面通过作者的研究工作详细介绍这一实验技术的具体内容、校核方法,以及此方法在国外叶轮机气动弹性领域的应用,希望推动其将来在国内气动弹性研究中的应用。

1 实验方法

根据Fransson[27]的描述,此方法可以解释如下。对一具有“2N+1”个叶片的压气机协调叶栅,叶片从“-N”到“+N”排列,参考叶片定义为叶片0,叶片+1与其吸力面紧邻,叶片-1与其压力面紧邻,图1给出只有7个叶片的示意图。箭头表示所有振动叶片(包括其自身)对参考叶片0的非定常气动影响,叶片0上无量纲非定常气动影响系数(此处以压力表征,叶片间相位角为σ),是所有振动叶片非定常压力影响系数线性叠加的结果。叶片0上非定常压力为复数形式以便分离时间相关项：

图1 压气机协调叶栅中参考叶片0上来自所有振动叶片的非定常气动影响Fig.1 Unsteady aerodynamic influences on the reference blade 0 from all blades in a tuned compressor cascade

因此得到协调叶栅叶片0上由N个振动叶片耦合的非定常压力系数为：

这里C˜ptc(N,0)表示叶片N振动对叶片0的非定常压力影响系数,假设其它叶片静止。当叶片+1领先叶片0时,叶片间相位角为正,对压气机而言对应于前行波波型。

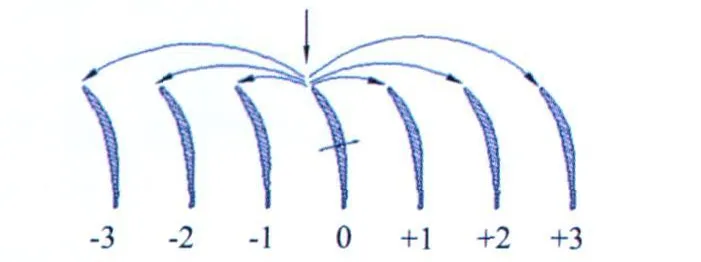
图2 振动叶片0在影响系数法叶栅中所有叶片上引起的非定常气动响应Fig.2 Unsteady aerodynamic influences acted on all blades in an ICM cascade from the oscillating blade

从分析的角度,这一技术是基于无限个叶片线性叠加的结果。但是,在实际情况下,影响系数(0, N)随着N的增加衰减很快,在叶片+1和叶片-1上,影响程度小一个数量级,见图3[12]中叶片0、叶片+1和叶片-1上的非定常压力影响系数的对比。因此,叶栅中3～5个叶片数据就足够构造等价协调叶栅数据tc。

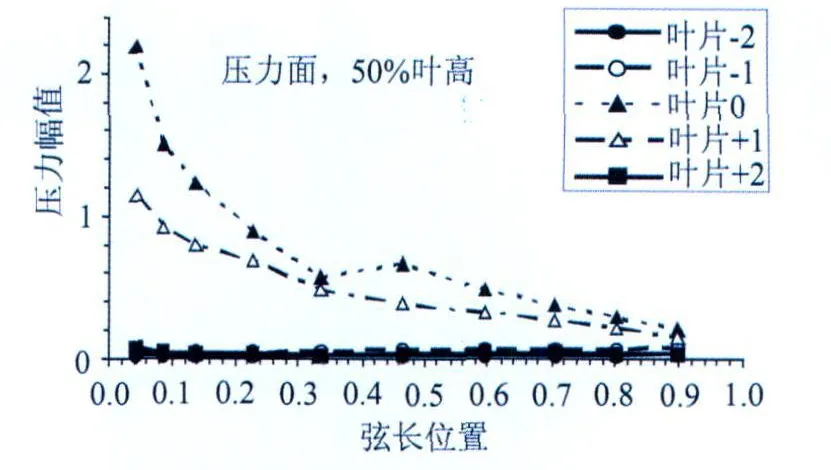
图3 影响系数法叶栅中由叶片0振动在中间5个叶片上引起的非定常压力幅值Fig.3 Unsteady pressures on the pressure surface of the middle five blades at midspan in an IC M cascade due to the oscillation of blade 0

此方法的要点如下：非定常压力影响系数Cp˜ic(0,N)称为“直接项”,沿叶片积分后分别为每个叶片对叶栅整体气动阻尼的贡献,见图4[12]。其物理含义是量化每个叶片对叶栅整体非定常气动响应的贡献,体现了每个叶片的相对重要性。由图可知,对参考叶片非定常气动响应影响最大的是由其本身的振动引起的,其次是与其压力面相邻的叶片-1,再其次是,与其吸力面相邻的叶片+1。而影响系数称为“耦合项”,积分为叶栅整体气动阻尼,对应于图4中各个叶片气动阻尼之和,此值随叶片间相位角变化(见图5),由图可知,叶片间相位角与折合频率对气动阻尼的影响具有耦合作用。折合频率的增加不仅提高了每个叶片间相位角下的气动阻尼,而且会减小最小气动阻尼(最不稳定状态,即易发生颤振状态)对应的叶片间相位角数值,由此推断,当折合频率足够高时,颤振发生时会对应负的叶片间相位角,即后行波波型(对于压气机而言)。而叶尖间隙对气动阻尼的影响就不与叶片间相位角的作用耦合(见图6),并且在最不稳定叶片间相位角(30°)下间隙流对气动阻尼的作用最强。对于给定的叶栅几何,折合频率和进口流动条件,影响系数法允许直接项和耦合项分开测量和评估。分解的“直接项”对认识每个叶片的相对重要性是有帮助的,而“耦合项”可以用来判断起颤点,可以提供强迫响应分析中的阻尼项。注意到叶片间相位角不是实验参数而仅仅出现在后处理中,从而大大减少了获得振动叶栅所有叶片间相位角下气动阻尼的工作量。为了更大程度上简化实验设备,只在振动叶片和一个静止叶片上装备测点[12],此静止叶片与其他静止叶片交换位置,以测量所有叶片位置处的非定常压力。

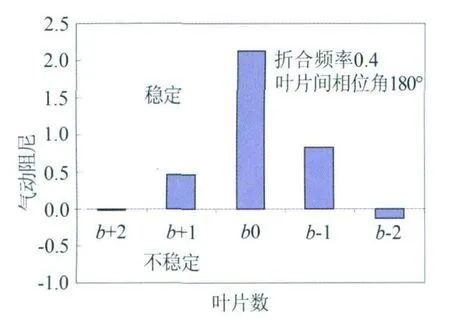
图4 来自中间五个叶片的气动阻尼分量Fig.4 Aero-damping components contributed by the middle five blades

图5 三个折合频率k下的整体气动阻尼Fig.5 Overall aerodynamic damping at three reduced frequencies

图6 三种叶尖间隙设置下整体气动阻尼对比Fig.6 Overall aerodynamic damping for three tip-gap settings

2 影响系数法校核

由于影响系数法假设叶片之间的非定常气动影响是线性叠加的,所以校核此法对相关流动的有效性是很重要的,通常从两方面进行：(一)检查收敛性,考察远离参考位置处叶片上的非定常压力的衰减率。(二)检验所关注的非定常流动的线性特征。一般是对比两组数据：由影响系数法得到的等价振动叶栅数据,和全部叶片按给定的叶片间相位角振动得到的协调叶栅数据[8,26]。这需要复杂的叶片驱振设备。也可以通过检测不同叶片振幅下非定常压力来验证[10]。如图7(对振幅归一化的压力幅值)和如图8[12](相位角)所示非定常流动具有显著的线性行为(详细内容参见文献[28])。

图7 对振幅归一化的非定常压力第一谐频幅值(20%和90%叶高)Fig.7 1st harmonic pressure amplitudes normalized by the corresponding vibration amplitudes on the oscillating blade (at 20%and 90%span)

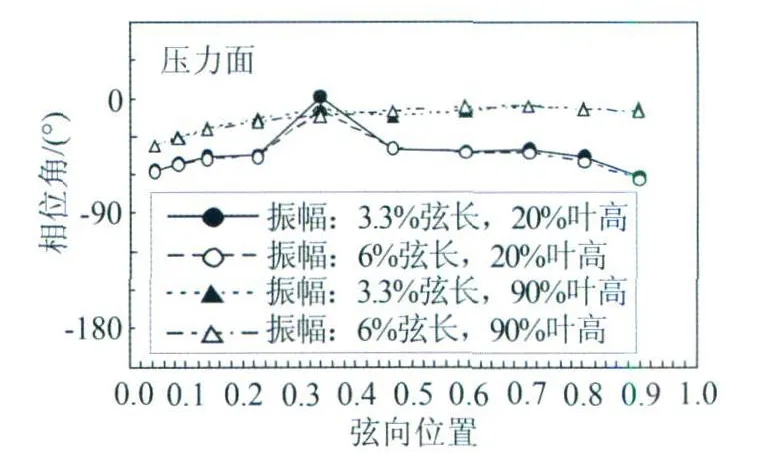
图8 非定常压力第一谐频相位角(20%和90%叶高)Fig.8 1st harmonic pressure phases on the oscillating blade(at 20%and 90%span)

国外的前期实验验证了该方法有效的几种情况：中亚声速马赫数下的附着流动[8];吸力面有小超声速区但无激波存在的高亚声速马赫数流动[29];叶片具有表面层流分离泡的流动[30]。但是对于非线性大分离流,影响系数法有其局限性[25]。

3 影响系数法应用

在过去的20年中,国外研究者运用该实验技术,旨在定量分析一些颤振参数,在考虑叶片间气动耦合情况下,对叶片非定常气动响应的影响。这些参数包括高亚声速和跨声速流下,真实的折合频率[8]、叶片表面定常载荷[15,29],叶片振动幅值[15]等,为经典的线性化平板叶栅理论的校核提供了验证数据。

由于颤振问题的复杂性,目前对于颤振发生机理还不清楚,参数化研究是气动弹性基础实验的优势。对于压气机/风扇叶片新结构,如小展弦比叶片[9,25]、跨声叶片[31]、复合材料风扇叶片,或颤振故障发生的非常规部件,如涡轮叶片[32],影响系数法最重要的作用是辨别影响这些结构气动阻尼的决定性参数,并评估这些参数的相对重要性,进而探讨颤振发生机理,在设计中指导叶片的气动弹性分析。例如,迄今为止,折合频率是判断叶轮机叶片颤振的主要设计参数,然而Nowinski[26]的研究表明,对于低压涡轮,叶片振动模态是决定颤振的最重要因素。

为校核不同的非定常气动模型,以及数值模拟方法与实验数据的相互校核,从而建立理论模型的有效性,Bölcs&Fransson编著了气动弹性标准算例集。收录的9个标准结构包括了涡轮和压气机叶片结构,从亚声、跨声到超声速流工况的非定常绕流实验数据以及不同理论模型模拟的计算结果。由于没有使用影响系数法,这些实验最多考核的叶片间相位角数也只有3～5个,有的甚至只有1个,这对于理解叶片与叶片之间的气动耦合效应,以及这一效应与其它影响参数对结构非定常气动响应的共同作用显然是不够的。使用影响系数法,可以很方便地考察任何结构/气动参数在所有叶片间相位角下对振动叶栅气动弹性稳定性的作用,以及这些参数的作用是否与叶片间相位角的作用相耦合。

对于亚声速流动下的经典气动弹性分析,除失速颤振外,大多使用欧拉法,但是对于跨声速流,Szechenyi[33]发现由叶片振动引起的激波运动对气动阻尼有显著影响,是叶片气动弹性不稳定的主要原因。如何高效求解N-S粘性方程并选取合适的湍流模型模拟跨声速流中激波/边界层干扰一直是数值模拟研究中的重点和难点。但是对层流分离泡这样的粘性效应,基础实验的研究表明[12]其对振荡叶栅非定常气动响应的影响只限制在局部区域,为时间线性化法有效模拟此类非定常流场提供了实验数据校核。

目前二维或准三维的气动弹性分析方法已经应用于国外工程界。但是基础实验结果[10]显示振动叶片每个横截面处的非定常压力与当地叶片振动幅值成非等比例关系,表明叶片表面的非定常气动响应沿叶高具有掺混的三维特征,此结论挑战了气动弹性分析准三维模型的可信程度。

以判断起颤点为目的气动弹性分析模型常常不包括叶尖间隙,只知道叶尖间隙流对气动效率有不利影响并且是旋转失速的重要成因之一。基础实验的结果表明[12]叶尖间隙对气动弹性稳定性的影响程度与折合频率(k)相当(对比图5和图6),以往不考虑叶尖间隙的气动弹性模型,给出的颤振预测是过稳定的,指出叶尖间隙模拟在气动弹性分析中的重要性。深入理解叶尖间隙流对气动弹性稳定性的作用机制,发展简单而精确的叶尖间隙非定常气动模型是基础实验和CFD研究者共同的任务。

目前,有数值模拟结果发现级间效应对颤振有影响,如上游静子排对转子排非定常压力波的反射与叶片振动引起的非定常压力波有耦合效应[34],对振动叶片起气动弹性稳定作用;来流激励与颤振也具有耦合效应[35]。这些研究结果指出新颤振分析系统的计算域不再是孤立的叶片排,而是叶片级甚至多级,为了提高计算效率,发展包括这些参数作用的简单非定常气动模型具有重要工程意义。深入理解这些关键参数对振动扰流非定常物理特征的影响,为非定常气动模型提供理论依据是目前叶轮机气动弹性研究者关注的挑战性难题。

对于可压流线性振荡叶栅,尤其是带有激波的跨声速流,由于风洞壁面或尾板的不利影响,叶栅很难产生叶片间定常流动的周期性[33],及行波模式下的非定常周期性[36-37],研究人员一直致力解决这一难题[38]。而影响系数法避免了线性叶栅采用行波模式遇到的困难,但需要通过有关声学处理克服风洞声学模态的不利影响[39]。因此,可压流动下影响系数法和环形叶栅配合[32],不可压流动下,影响系数法和线性叶栅结合[34]都是最佳选择。低速流下,低的振动频率,选用外置压力传感器结合管传递函数修正[40]测量叶片表面的非定常压力,可以同时提高测量参数的空间和时间分辨率,为数值模拟方法提供更详细和精确的试验数据。

时至今日,国内叶轮机械气动弹性领域全三维非定常流动数值模拟技术[41-42]与尚未开展的基础验证实验之间的不平衡,特别是三维振动结构非定常流动实验数据的缺乏,很大程度上局限了气动弹性数值模拟方法的工程应用,而影响系数法是开展叶轮机气动弹性基础校核实验简单有效的方法。

4 结 论

介绍的实验技术是获取不同叶片间相位角下振动叶片表面非定常气动响应的实验模型,以一种简单的方式考虑了叶片间的气动耦合,是叶轮机气动弹性领域参数化基础研究的有效手段。提到的前期气动弹性实验结果表明,只要对相关非定常流动检测其有效性,此方法可以探索颤振物理机制,尤其是对于新设计或改进的叶片结构可以方便地识别其最重要的颤振影响参数。总之,以探究叶片颤振发生机理为宗旨的基础性实验,对于指导、改进和完善以数值模拟为主要手段的叶片颤振设计体系尤为重要,此方法对工程设计人员和CFD程序开发者都十分有用。

[1] SHANNON J F.Vibration problems in gas turbines, centrifugal and axial flow compressors[R].A.R.C., R&M 2226,1945.

[2] HALL K C,LORENCE C B.Calculation of three-dimensional unsteady flows in turbomachinery using the linearized harmonic Euler equations[J].Journal of Turbomachinery,1993,115：800-809.

[3] NING W,HE L.Computation of unsteady flows around oscillating blades using linear and nonlinear harmonic Euler methods[J].Journal of Turbomachinery, 1998,120：508-514.

[4] HE L.An Euler solution for unsteady flows around oscillating blades[J].Journal of Turbomachinery,1990, 112：714-722.

[5] CHEN J P.Unsteady three-dimensional thin-layer Navier-Stokes solutions for turbomachinery in transonic flow[D]. PhD thesis,Mississippi State University,USA,1991.

[6] SADEGHI M.Parallel computation of three-dimensional aeroelastic fluid-structure interaction[D].University of California,Irvina,USA,2004.

[7] BÖLCS A,FRANSSON T H.Aeroelasticity in turbomachines comparison of theoretical and experimental cascade results[R].Communication du Laboratoire de Thermique Appliquée et de Turbomachines,No.13, Lausanne,EPFL,1986.

[8] BUFFUM D H,FLEETER S.Investigation of oscillating cascade aerodynamics by an experimental influence coefficient technique[R].AIAA 88-2815,1988.

[9] HAYDEN J,CAPECET V R,LEPICOVSKG J.The influence coefficient method for airfoils oscillating in pitching motion at large mean incidence[R].AIAA 2002-4087,2002.

[10]BELL D L,HE L.Three-dimensional unsteady flow for an oscillating turbine blade and the influence of tip leakage[J]. Journal of Turbomachinery,2000：122(1)：93-101.

[11]QUEUNE O JR,HE L.Experimental study of 3D unsteady flow around oscillating blade with part-span separation[J].Journal of Turbomachinery,2001：123(3)：519-525.

[12]YANG H,HE L.Experimental study on linear compressor cascade with three-dimensional blade oscillation [J].Journal of Propulsion and Power,2004,20(1)：180-188.

[13]FRANSSON T H,BORG R.Summary of aerodynamic test methodologies used in linear and annular wind tunnel cascades and single and multistage cold flow rotating turbine experiments[R].Internal report,LT T-EPTLausanne,Switzerland,1992.

[14]HALLIWELL D G,NEWTDN S G,LIT K S.A study of unsteady pressures near the tip of a transonic fan in unstalled supersonic flutter[J].Journal of Vibration,A-coustics,Stress,and Reliability in Design,1984,106(2)：198-203.

[15]FREY K K,FLEETER S.Oscillating airfoil aerodynamics of a rotating compressor blade row[J].Journal of Propulsion and Power,2001,17(2)：232-239.

[16]SANDERS A J,HASSAN K K.Experimental and numerical study of stall flutter in a transonic low-aspect ratio fan blisk[R].ASM E GT2003-38353,2003.

[17]LANE F.System mode shapes in the flutter of compressor blade rows[J].Journal of the Aeronautical Science,1956,23(1)：54-66.

[18]CA RTA F O,St.HILAIRE A O.Effect of interblade phase angle and incidence angle on cascade pitching stability[J].Journal of Engineering for Power,1980,102 (2)：391-396.

[19] KOBAYASHI H.Effects of shock waves on aerodynamic instability of annular cascade oscillating in a transonic flow[J].Journal of Turbomachinery,1989,111 (2)：222-230.

[20]BUFFUM D H,FLEETER S.The aerodynamics of an oscillating cascade in a compressible flow field[J]. Journal of Turbomachinery,1990,112(4)：759-767.

[21]FLEETER S,NOVICK A S,RIFLEL R E,et al.An experimental determination of the unsteady aerodynamics in a controlled oscillating cascade[J].Journal of Engineering for Power,1977,99(1)：88-96.

[22] FRANSSON T H.Analysis of experimental time-dependent blade surface pressures from an oscillating turbine cascade with the influence-coefficient technique [R].ASM E 90-GT-225,1990.

[23]HANAMURA Y,TANAKA H,YAM AGUCHI K.A simplified method to measure unsteady forces acting on the vibrating blades in cascade[J].Bulletin of the JSME,1980,23(180)：880-887.

[24]WATANABE T,KAJI S.Experimental study on unsteady aerodynamic characteristics of an oscillating Cascade with tip clearance[J].JSME international Journal, 1988,31(4)：660-667.

[25] EHRLICH D A,FLEETER S.Incidence effects on chordwise bending cascade unsteady aerodynamics[J]. AIAA Journal,2000,38(2)：284-291.

[26]NOWINSKI M,PANOVSKY J.Flutter mechanisms in low pressure turbine blades[R].ASME 98-GT-573, 1998.

[27]FRANSSON T H.Basic nomenclature of time-dependent internal aerodynamics[R].VKI Lecture Series on Aeroelasticity in Axial-Flow Turbomachines,1999.

[28]杨 慧,何 力,王延荣.压气机线性振荡叶栅气动弹性试验研究(一)：非定常气动响应[J].航空学报, 2008,29(4)：180-188.

[29]KÖRBÄCHER H,BÖLCS A.Experimental investigation of the unsteady behavior of a compressor cascade in an annular ring channel[R].Proceedings of the 7th ISUAAT,Fukuoka,Japan,1994.

[30]HE L.Unsteady flow in oscillating turbine cascades：part1-linear cascade experiment[J].Journal of Turbomachinery,1998,120(2)：262-268.

[31]LEPICOVSKY J,MCFARLAND E R,CAPECE V R, et al.Unsteady pressures in a transonic fan cascade due to a single oscillating airfoil[R].ASM E GT-2002-30312,2002.

[32]VOGT D M,FRANSSON T H.Experimental investigation of mode shape sensitivity of an oscillating LPT cascade at design and off-design conditions[R].ASM E GT2006-91196,2006.

[33] SZECHENYIE.Understandingfan bladeflutter through linearcascadeaeroelastictesting.AGARD M anual on Aeroelasticity in Axial-Flow Turbomachines [R].Volume 1-Unsteady Turbomachinery Aerodynamics,AGARD-AG-298,1987.

[34]HUANG X Q.Three-dimensional unsteady flow in oscillating turbine blade row[D].PhD thesis,Durham U-niversity,Durham,UK,2006.

[35] FREY K K,FLEETER S.Combined/simultaneous gust and oscillating compressor blade unsteady aerodynamics[J].Journal of Propulsion and Power,2003,19 (1)：125-134.

[36]CARTA F O.Unsteady aerodynamics and gapwise periodicity of oscillating cascaded airfoils[J].Journal of Engineering for Power,1983,105(3)：565-574.

[37]BUFFUM D H,FLEETER S.Wind tunnel wall effects in a linear oscillating cascade[J].Journal of Turbomachinery,1993,115(1)：147-156.

[38]LEPICOVSKY J,CHIMA R V,MCFARLAND E R, et al.On flowfield periodicity in the NASA transonic flutter cascade[J].Journal of Turbomachinery,2001, 123(3)：501-509.

[39]BUFFUM D H,FLEETER S.Effect of wind tunnel acoustic modes on linear oscillating cascade aerodynamics [J].Journal of Turbomachinery,1994,116(3)：513-524.

[40]杨 慧,西姆斯-威廉姆斯戴维,何 力.非定常压力测量中信号失真的管传递函数修正方法[J].实验流体力学,2007,21(3)：70-75.

[41]金 琰,袁 新.三维透平叶片扭转颤振问题的流固耦合数值研究[J].工程热物理学报,2004,25(1)：41-44.

[42]黄秀全,周新海.利用傅立叶方法求解振荡叶栅非定常流[J].西北工业大学学报,2008,26(3)：357-361.