纳米流体黏度影响因素的试验研究

武婷婷, 骆仲泱, 倪明江, 魏 葳, 冯钊赞, 王 涛

(浙江大学 热能工程研究所,能源清洁利用国家重点试验室,杭州 310027)

随着技术的飞速发展和能源问题的突出,迫切需要新型换热流体来提高换热效率,减少能量消耗.但水、机油和乙二醇等传统换热工质的导热系数较小,影响了强化传热的效果.常温下大多数固体材料的导热系数比流体材料大,因此,如果将固体颗粒加入流体中,换热效果将会得到强化,但是毫米或微米级的固体粒子悬浮液会引起管道堵塞、磨损和颗粒沉淀等问题.近年来,纳米材料和技术的快速发展使固体颗粒强化流体传热成为了可能.1995年美国A rgonne国家试验室的Choi[1]在国际上首次提出“纳米流体”的概念,这一概念已被广泛接受[2],即以一定的方式和比例在液体中添加纳米级金属或金属氧化物粒子,形成一类新的传热冷却工质,这是纳米技术应用于传热学中的创新性研究.

水和乙二醇是纳米流体最常用的基液,有各自不同的特性,若将两者以不同比例混合的混合液作为基液,可以起到优势互补的效果,制备得到的流体会呈现不同的物性.尤其在一些寒冷的地区,需要换热流体的冰点较低,乙二醇水溶液可以满足,并且现在车载防冻液大部分也在使用乙二醇水溶液[3-4].Das[5]研究了体积分数均为 8%,粒径分别为 20 nm、50 nm 和100 nm的SiO2-乙二醇/水纳米流体在不同温度下的黏度,发现粒径为100 nm的SiO2纳米流体的黏度最小.

本文的研究目的是探索纳米流体黏度的影响因素,即研究以去离子水(DW)、乙二醇(EG)和不同配比的混合液为基液的纳米流体的黏度随粒径、温度和浓度的变化规律.

1 试验介绍

1.1 流体制备

与传统的固液混合物相比,纳米流体较小的颗粒尺寸和在基液中的布朗运动可以改善悬浮液的分散均匀性,使其具有良好的稳定性.制备纳米流体总体上有2种方法[6]:(1)一步法制备纳米流体,指在制备纳米颗粒的同时将其分散在基液中;(2)两步法制备纳米流体,先制备出纳米粒子,然后通过超声波振动、添加活性剂或分散剂、改变溶液pH等方法,将制备得到的纳米粒子均匀分散到液体中,最终形成纳米流体悬浮液.

笔者采用两步法制备纳米流体,不添加分散剂,即将纳米粉体加入到预先准备好的基液中,先充分搅拌30 m in使其混合均匀,再超声振荡30 min,制备得到稳定悬浮的纳米流体.制备流程见图1.

图1 纳米流体制备流程图Fig.1 Flow chart of nanofluid preparation

1.2 黏度测量

黏度测量选用不同测量范围的乌氏黏度计,并用精密恒温槽进行控温(精度为0.01 K)来实现.首先对去离子水的黏度值进行标定,再测量流体的黏度.同时重复多次测量,重现性很好.纳米流体的粒径分布由英国M alven激光粒度分析仪(Nano-S90)测得.

1.3 试验仪器

试验采用的试剂和仪器见表1.

表1 试验所采用的试剂和仪器Tab.1 M aterials and apparatus applied in experiment

2 结果与分析

采用乙二醇和水的混合液作为基液,研究颗粒粒径和温度对流体黏度的影响,并指定3种基液,研究纳米流体黏度随流体浓度的变化规律.

2.1 颗粒粒径对黏度的影响

图2 体积分数为0.8%的SiO2纳米流体黏度与粒径的关系Fig.2 V iscosity of 0.8%SiO2 nanofuild varying with nanoparticle size

图2给出了基液和3种不同粒径的纳米流体黏度的变化规律,其中横坐标为基液(水和乙二醇的混合液)中乙二醇的体积分数.由图2可以看出,添加颗粒后的纳米流体黏度提高,但其变化趋势基本与基液一致.在基液相同的情况下,粒径为7 nm的纳米流体的黏度明显较大,这是因为粒子越小,相同体积份额情况下粒子数越多,粒子间距离越近,粒子间的相互作用越大,并且纳米流体流动时,颗粒不得不避开其他的颗粒,为克服内摩擦阻力需消耗一定的能量,因而粒子数越多,黏度就越大.相比较,粒径为30 nm和40 nm的纳米流体的黏度差别不是很大.当基液为纯乙二醇时,3种粒径纳米流体的黏度较接近,在纯乙二醇中颗粒分散较稳定均匀,因此,相对基液来说,纳米流体的黏度增加也都较小,增加率为3.4%左右.

2.2 温度对黏度的影响

图3中3条虚线分别表示20℃、25℃和30℃基液的黏度,3条实线分别表示这3个温度下颗粒粒径为7 nm、体积分数为0.8%的SiO2纳米流体的黏度.由图3中虚线可以看出,随着温度的升高,基液的黏度逐渐减小,并且乙二醇的体积分数越高,黏度减小的幅度越大,当基液为纯乙二醇时,黏度受温度影响最明显.

图3 基液和纳米流体的黏度随温度的变化Fig.3 V iscosity of base fluid and nanofluids varying w ith temperatu re

在同一温度下,由于纳米颗粒的小尺寸效应和界面效应,使得固体颗粒与液体分子之间的相互作用增强,流体的黏度有所增大.随着温度的升高,纳米流体的黏度减小,一方面温度影响纳米颗粒的布朗运动,温度越高,颗粒的运动越剧烈,微运动对黏度有重要影响;另一方面纳米流体的黏度受温度影响的趋势基本与基液相同,说明基液是纳米流体黏度的重要影响因素.

图4给出了纳米流体的相对黏度随温度的变化.由图4可知,在试验范围内,纳米流体的相对黏度与温度的关系不大,而与基液中乙二醇的体积分数有关.纯乙二醇基纳米流体的相对黏度增加最小,仅为4%,但是相对黏度并没有随基液中乙二醇体积分数的增大呈现单调减小的变化趋势,这可能与基液为混合液有关,颗粒在混合液中分散的情况较复杂.

图4 纳米流体的相对黏度随温度的变化Fig.4 Relative viscosity of variousnanofluids varying w ith temperatu re

2.3 颗粒体积分数对黏度的影响

图5给出了3种基液的纳米流体黏度随颗粒体积分数的变化.纳米颗粒为粒径7 nm的SiO2,基液分别为DW、EG以及EG/DW(EG的体积分数为50%),用相对黏度表示基液黏度的增加值[7].

图5 纳米流体黏度与颗粒体积分数的关系Fig.5 V iscosity of nanofluid varying w ith volumetric fraction of nanoparticles

由图5可以看出,当体积分数相同时,SiO2-DW纳米流体的相对黏度均高于SiO2-EG纳米流体的相对黏度,即相对基液来说,SiO2-EG纳米流体的黏度增加较小.这是由于EG基液黏度大,SiO2对于EG的亲液程度大于DW,因此在EG中分散性好,容易稳定存在,团聚程度较小,则黏度增加较小.由图5还可以看出,以EG、DW 为基液的纳米流体的黏度随颗粒体积分数的增加基本呈线性增长,这也符合Einstein[8]提出的针对体积分数较小的纳米流体的黏度模型.在低浓度时,以 φ(EG)∶φ(DW)=1∶1混合溶液为基液的纳米流体的黏度曲线介于以纯EG和以纯DW为基液的纳米流体的黏度曲线之间,即其相对黏度介于纯EG基和纯DW基纳米流体之间,这是因为以纯EG为基液的纳米流体的分散稳定性较好,黏度增加最小,以EG和DW的混合溶液为基液的纳米流体的分散稳定性次之,以纯DW基为基液的纳米流体的分散稳定性最差,颗粒团聚程度较大,黏度增加也就最大.

2.4 纳米颗粒团聚对黏度的影响

对于低浓度纳米流体,根据Einstein(1911)假设,在无限稀释的线性悬浮体中,悬浮颗粒是刚性球,表面无负载电荷,且颗粒之间无相互作用,相对黏度是悬浮粒子体积分数的简单函数:

式中:ηr为相对黏度;η为纳米流体的动力黏度;ηbf为基液的动力黏度;Υ为颗粒的体积分数.

Batchelor(1977)考虑布朗运动,提出适用于体积分数不大于10%的纳米流体黏度的计算公式:

对于体积分数大于10%的纳米流体,涵盖全部体积分数的半经验公式由K rieger和Dougherty(1959)提出:

式中:Υm为最大颗粒填充分数,球状颗粒取0.605.

对比试验数据和 Einstein、Batchelor、K-D[8]公式计算得到的黏度值(图6)可知,当体积分数很小时,经典模型的计算值均小于试验值,这主要是因为经典相对黏度计算公式仅是基液和体积分数的函数,没有考虑纳米流体中的颗粒团聚、颗粒表面的水化膜等因素,而这些因素的客观存在可增大纳米流体的相对黏度[7].

图6 纳米流体相对黏度试验值与计算值的对比Fig.6 Com parison of relative nanofluid viscosity betw een experimental and calculated resu lts

考虑到纳米流体中的颗粒团聚现象,Chen提出修正的K rieger&Dougherty公式[8],用有效体积浓度Υa替代实际体积浓度 Υ,根据分形理论得:

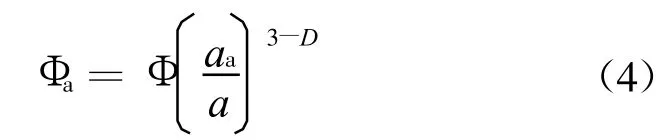
则

考虑到纳米流体团聚结构对相对黏度的影响,由式(5)得到纳米流体相对黏度的计算公式[9]:

式中:aa为团聚体半径;a为颗粒半径;D为团聚体的分形维数,对于纳米悬浮液,其值为1.8～2.5.

以EG为基液的纳米流体,a a/a=14.57;以DW为基液的纳米流体,a a/a=18.42,其中a a由Malvern-Zetasizer NanoS90得到,将其代入修正的K-D公式,计算结果如图 6中的 K-D(EG),K-D(DW)所示,与试验测得的数据较吻合.当颗粒体积分数小于1%时,以混合液为基液的纳米流体的相对黏度与以EG、DW为基液的纳米流体较接近,当体积分数大于1%时,黏度急剧增大.

以上现象的原因可以从EG和混合液为基液的纳米流体的粒径分布图(图7和图8)得出.由图7可知,当颗粒体积分数为0.1%时,分别以EG和混合液为基液的纳米流体的粒径分布相近,宏观表现为两者的相对黏度基本相同.由图8可知,当颗粒体积分数为1.6%时,以基液为混合液的纳米流体的粒径分布范围较宽且粒径较大,团聚程度明显增加,从而导致其黏度增加较大.

图7 0.1%体积分数的流体中纳米颗粒的激光粒度分布Fig.7 Laser particle-size distribution for nanoparticles of 0.1%volumetric fraction

如果团聚体的尺寸与纳米流体的体积分数有关,结合式(6),aa/a的比值可由每个流体的体积分数计算得到,计算结果见图9.

由图9可知,基液为纯水和纯乙二醇的纳米流体的团聚比变化趋势相似,均随体积分数的增加略微增大,但水基的团聚程度均高于乙二醇基.然而,随着体积分数的增大,以混合液为基液的纳米流体的团聚程度急剧增加.将纳米流体黏度提高的原因归结于纳米颗粒的团聚,不同的黏度是由于纳米颗粒聚集状态(即团聚体的微观结构)不同,这种微结构就是颗粒本身和基液相互作用的表现,不容忽视基液的影响.

图8 1.6%体积分数的流体中纳米颗粒的激光粒度分布Fig.8 Laser particle-size distribution for nanoparticles of 1.6%volumetric fraction

图9 纳米流体体积分数与团聚比的关系Fig.9 a a/a ratio vs.volumetric fraction of nanoparticles

3 结 论

(1)两步法制备纳米流体并不能分散颗粒到原始粒径,颗粒在基液中以团聚形式存在,这对黏度有不利影响.

(2)以水、乙二醇或两者的混合液为基液的纳米流体,在相同基液的条件下,颗粒尺寸越小,黏度越大;基液中EG体积分数越大,纳米流体黏度受温度影响越显著,且流体温度升高,黏度减小,但相对黏度与温度无关,仅与基液有关.

(3)以水、乙二醇为基液的纳米流体的相对黏度随颗粒体积分数的增加基本呈线性增加,与修正的K-D公式较吻合;而以乙二醇/水(乙二醇体积分数为50%)为基液的纳米流体的相对黏度在颗粒体积分数大于1%时急剧增大.

[1] CHOI S U S.Developments and app lications of nonnew tonian f low s[J].American Society of M echanical Engineering,1995,231:66-99.

[2] 商福民,刘登瀛,冼海珍,等.自激振荡流热管内 Cu-水纳米流体的传热特性[J].动力工程,2007,27(2):233-236.SH ANG Fum in,LIU Dengying,XIAN H aizhen,et al.H eat transfer characteristics of Cu-Water in self-exciting mode-oscillating flow heat pipe[J].Journa l of Power Engineering,2007,27(2):233-236.

[3] CHOISU S,YU W,HULL J R,etal.Nanofluids for vehicle thermal management[C]//Vehicle Thermal Management Systems Conference&Exhibition.Nashville:SAE,2001.

[4] MCQU ISTON F C,PARKER J D,SPITLER J D.H eating,ventilating and air conditioning:analysis and design[M].New York:John W iley&Sons,Inc.,2005.

[5] NAMBURU P K,K ULKARNI D P,DANDEKAR A,et al.Experimental investigation of viscosity and specific heat of silicon dioxide nanofluids[J].M icro&Nano Letters,2007,2(3):67-71.

[6] 王补宣,李春辉,彭晓峰.纳米颗粒悬浮液稳定性分析[J].应用基础与工程科学学报,2003,11(2):167-173.WANG Buxuan,LIChunhui,PENG Xiaofeng.Stability of nano-particle suspensions[J].Journal of Basic Scienceand Engineering,2003,11(2):167-173.

[7] 李长江,尹衍升.纳米流体流变特性研究最新进展[J].山东陶瓷,2009,32(3):14-17.LIChangjiang,YIN Yansheng.The latest achievements of nanofluid rheological properties research[J].Shandong Ceram ics,2009,32(3):14-17.

[8] CHEN H aisheng,W ITHARANA Sanjeeva,JIN Yi,et a l.Predicting thermal conductivity of liquid suspensions of nanoparticles(nano fluids)based on rheology[J].China Particuology,2009,7(2):151-157.

[9] PASTORIZA-GALLEGO M J,CASANOVA C,PARAMO R,eta l.A study on stability and thermophysical properties(density and viscosity)of A l2O3in w ater nano fluid[J].Journa l of App lied Physics,2009,106(6):301-309.