悬挂式轨道设计探讨

王巨民 胡友民

悬挂式轨道是矿业、民爆行业中常用的钢结构构件[1]，但目前关于其设计的介绍并不多。现有的文献多关注于悬挂式轨道的强度分析，而其安装方法及固有频率对整体功能影响的分析尚处于空白状态[2，3]。本文结合工程背景对悬挂轨道的设计进行探讨。

1 工程概况

某一隧道，宽4m，高3.5 m，总长为100m，顶部呈半圆形。隧道的左右两侧及顶部壁面均由混凝土喷涂到岩石表面形成，混凝土厚约 15mm。因业主需求，在隧道顶部搭建一条小车轨道。小车在轨道上往复移动，移动范围为 90m。正常工作时要求小车的移动速度为 1m/s;当需要快速定位时，要求小车能够以最大20m/s的速度定位到指定位置。

现小车的结构已定，要求完成轨道的设计。小车要求轨道的横截面与冷弯等边槽钢GB/T 6723-1986 160×80×5相同。在轨道横截面不能更改的情况下，设计重点在于保证在空间有限的隧道内完成大跨度轨道的安装以及单跨轨道长度的选择。

2 轨道安装形式探讨

为了便于加工、运输和安装，轨道用多节冷弯等边槽钢拼接而成。为了改善在小车作用下轨道的应力及变形情况，在每节槽钢上设置两个吊挂点。吊挂点在轨道长度方向上均匀分布。为了保证轨道表面平整、光滑，在相邻两节槽钢的接缝处进行打磨和调整。考虑到隧道的壁面并不规则，轨道平面与隧道顶部之间的距离应柔性可调。隧道壁面的混凝土喷涂材料难以直接承担轨道及小车的重量，因此将直径为 20mm的钢筋打入隧道顶部作为承载结构件。在每个吊挂点上方打入 2根钢筋，打入足够的深度以承担轨道与小车的重量。将导轨吊挂结构连接到 2根钢筋的下端，吊挂点在轨道长度方向上的位置通过钢筋打入点的位置来调整，轨道平面与隧道顶部之间的距离通过钢筋与吊挂结构的连接点位置来调整。

3 单跨轨道长度选择

在结构系统中，当一个激振频率与固有频率相接近，就会使系统发生共振，整个系统处于失效或准失效状态。由系统共振引起的疲劳破坏广泛存在于受冲击、瞬态或随机载荷作用的各种结构之中。共振时，结构的动应力大、寿命短，显得更加危险[4]。

在整个轨道系统中，当小车在固定轨道上移动时，每经过相邻两段单跨轨道的接缝处就会产生一次冲击，该冲击的频率即为激振频率。激振频率与小车的运行速度及单跨轨道长度有关。在小车最大速度已定的情况下，在选择单跨轨道长度即每节槽钢长度时应考虑可能引起的激振，避免系统发生共振。下面分析单跨长度为4m，5m，6m和7m，总长度为90m左右的悬挂式轨道的固有频率，为槽钢长度选择提供设计依据。

3.1 建立轨道有限元模型

根据工程实际需求及轨道安装形式，利用SolidWorks软件建立悬挂式轨道的三维简化模型，并通过程序接口导入ANSYS Workbench软件，如图1所示。

轨道选材为冷弯等边槽钢GB/T 6723-1986 160×80×5，吊挂结构简化为两根直径为20mm的钢筋，长度统一为0.8m，其上表面与水平面平行。相邻吊挂点之间的距离为每节槽钢长度的1/2，吊挂点与相邻槽钢接缝的距离为每节槽钢长度的 1/4。设置轨道及钢筋的材料参数为:杨氏模量2e+005MPa;泊松比0.3;密度7.85e-006 kg/mm3。采用自由网格划分方法，悬挂式轨道的有限元模型如图 2所示。

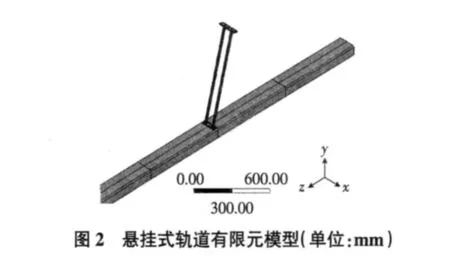
3.2 轨道固有频率分析

针对每节槽钢长度为4m，5m，6m和 7m，轨道总长度分别为92m，90m，90m和91m四种情况，分析悬挂式轨道的固有频率，分析结果如表1所示。

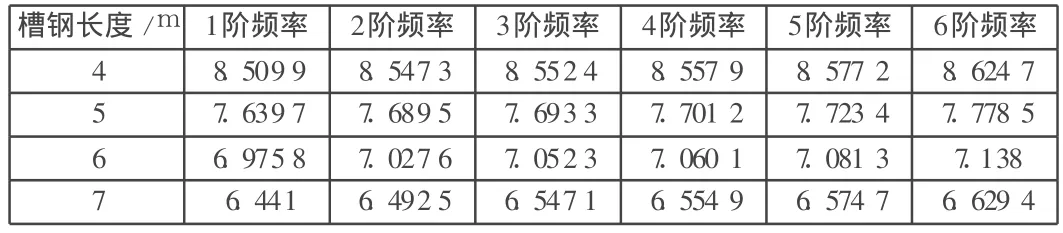
表1 固有频率分析结果 Hz

忽略总长度的微小差异对分析结果的影响，可以看出，随着每节槽钢长度的增长，悬挂式轨道的固有频率依次减小。

3.3 轨道长度选择

从理论上来说，固有频率与激振频率两者的比值大于 2时，相互的共振响应就较小(称倍频法则)，若固有频率重合或接近时，将出现共振现象[5]。因此，为了避免共振，要求激振频率小于1阶固有频率的 1/2。

小车最大运行速度v=20m/s，每节槽钢长度L=4m时，激振频率f为:

同理，当槽钢长度为5m，6m，7m时，激振频率分别为:4.00Hz，3.33Hz，2.86Hz。由以上分析可见，当每节槽钢长度为6m，7m时能够满足此要求。为了便于轨道的制造、运输和安装，选取每节槽钢长度为6m。

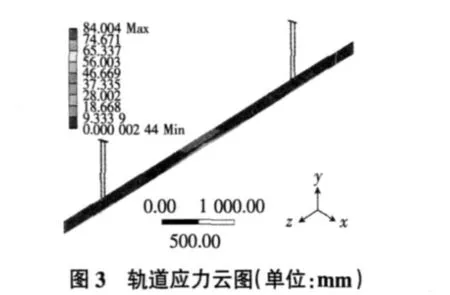
4 轨道强度校核

经以上讨论初步确定每节槽钢长度，利用ANSYSWorkbench软件对其进行强度校核。校核结果显示，当小车位于相邻两节槽钢的接缝处时，轨道的应力最大。如图 3所示，最大应力值为84MPa，小于材料的许用应力值，轨道强度满足要求。

5 结语

结合悬挂式轨道的应用背景，对轨道的安装形式进行了讨论。利用SolidWorks软件建立三维简化模型，借助ANSYSWorkbench软件进行固有频率分析，对轨道强度进行校核。分析结果表明:每节槽钢长度越长，轨道的固有频率就越低，而允许的小车最高速度增大，确定每节槽钢的合理长度为 6m。现已完成该悬挂式轨道的设计与加工，工程已进入安装阶段。

[1] 陈中亿.工业炸药悬挂式轨道输送车系统的安全性研究[J].爆破器材，2010，39(5):34-37.

[2] 孙世田.悬挂吊车悬挂点的受力特性与合理形式[A].第六届空间结构学术会议论文集[C].1992.

[3] 丁芸孙.悬挂吊车轨道与节点的设计探讨[A].第十一届空间结构学术会议论文集[C].2005.

[4] 张义民，宿苏英，李 鹤，等.随机连续梁弯曲振动系统的频率可靠性分析[J].应用力学学报，2007，24(1):133-136.

[5] 李朝旭.电子设备的抗振动设计[J].电子机械工程，2002，18(1):51-55.