配电网潮流计算中的分布式电源建模*

彭 彬,刘 宁,吴 迪

(1.鲁泰纺织股份有限公司,淄博 255100;2.天津陈塘热电有限公司,天津 300072)

近年来,分布式发电技术日益为学术界和工业界所关注,由于大量并网运行分布式电源的存在,对配电网潮流计算提出了更高要求[1～4]。当配电系统中引入分布式电源后,引起了配电线路中传输的有功和无功功率大小和方向的改变,配电系统成为一个多电源系统,而且不一定能维持严格的辐射状结构。因此,在进行潮流计算时,必须针对不同的节点类型采用不同的处理方法。

分布式发电系统一般通过以下几种方式接入配电网络。(1)通过异步发电机直接接入。如:异步发电机风力发电系统等。由于异步发电机没有励磁系统,需从系统中吸收大量的无功,其无功的大小与机端电压有关,因而需在潮流计算中做特殊处理。(2)通过同步发电机直接接入。如:双轴微型燃气轮机发电系统。由于采用同步发电机并网,一般励磁电压可调,故其处理方式与传统方法相同,可处理为PV节点。(3)通过电力电子装置接入。如:光伏发电系统、燃料电池发电系统、单轴微型燃气轮机发电系统。由于电力电子装置的运行方式及控制策略不同,其节点类型的选取要进行综合考虑。

本文针对常见的分布式发电并网系统、如微型燃气轮机并网系统、风力发电系统、燃料电池与光伏并网发电系统等,从并网结构及运行方式入手,分析其并网模型,建立了各自潮流计算数学模型。

1 微型燃气轮机系统模型

微型燃气轮机发电系统主要有两种结构,一种为分轴结构,另一种为单轴结构。分轴结构的动力涡轮与燃气涡轮采用不同转轴,动力涡轮通过变速齿轮与发电机相连,因此可直接并网运行;单轴结构的压气机、燃气涡轮与发电机同轴,发电机转速高,需通过变流器将频率转化为工频后并网。

1.1 分轴微型燃气轮机系统

分轴微型燃气轮机通过同步发电机直接并网,一般采用有励磁调节能力的同步发电机作为接口具有两种励磁控制方式,即电压控制和功率因数控制。采用电压控制的分布式电源在潮流计算中可作为PV节点处理,采用功率因数控制的分布式电源可作为PQ节点处理。因此,分轴微型燃气轮机系统在配电网潮流计算中,仍可按传统方式进行处理。在潮流迭代过程中,若PV节点无功越限,则将其转换成对应的PQ节点。如在后续迭代中又出现该节点电压越界,重新将其转换成PV节点。

1.2 单轴微型燃气轮机系统

单轴微型燃气轮机由于转速较高,高频量不能直接并网,需通过变流器变换为工频量后并网。常见的变流器拓扑结构有两种,如图1所示。

图1 变流器拓扑结构Fig.1 Topology of converter

通过整流器后,系统被分成了直流与交流两部分,可将交流部分与直流部分进行等效,一般处理如下[5]:交流系统中,整流器等效为△型负荷,逆变器等效为△型电源;直流系统中,整流器等效为直流电源,逆变器等效为直流负荷。图2给出了详细的等效模型。

图2 交流系统与直流系统等效模型Fig.2 Equivalentmodel of AC system and DC system

对于电流型的PWM变流器(整流器与逆变器),也存在类似的关系式成立,因而,二极管不可控整流器及电流型PWM变流器都可看作有功输出和注入电网电流恒定的PI节点。相应的无功功率可由前次迭代得到的电压、恒定的电流幅值和有功功率计算得出[2]:

整流器侧若采用二极管不控整流器,则有:

电压型PWM变流器在联网运行时可作为常规的PV节点处理。当系统脱离主网处于孤岛运行时,需分布式电源支撑系统的电压与频率,分布式电源相当于常规电力系统的平衡母线,因此孤岛运行时电压型PWM变流器还可作为节点(平衡节点)。电力电子变流器节点类型总结见表1。

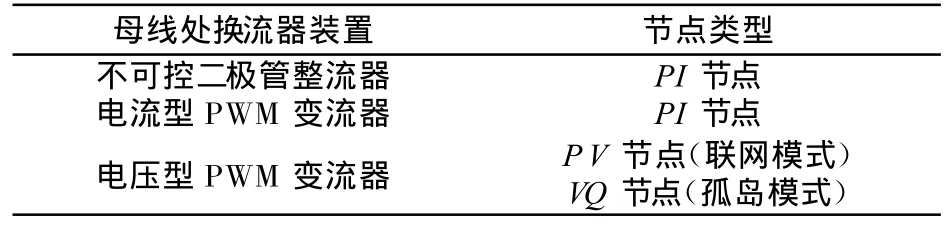
表1 电力电子换流器节点类型Tab.1 Node typeo f power electronics converter

2 风力发电系统模型

风力发电系统以异步电机直接并网发电系统和双馈发电系统较为常见。由于运行方式与控制策略各有不同,因此节点形式也各有不同。

2.1 异步电机直接并网

早期风力发电一般采用异步发电机并网运行,异步发电机靠电网提供无功功率建立磁场,没有电压调节能力。文献[6]将风电场在潮流计算中视为PQ节点,即根据有功功率和给定的功率因数直接计算得到无功功率。这种模型优点是处理简单,对现有潮流程序几乎无需改动,缺点是模型过于粗略。由于风电场吸收的无功功率随系统的运行情况不断变化,风电场的功率因数在不同系统运行方式下是变化的,因此采用这种模型将使计算结果不够准确。文献[7]提出一种RX迭代模型,把异步发电机的转差表示成机端电压和有功功率函数,给定初始转差和风速,由异步机等效电路写出异步机等效阻抗Z=R+jX,将发电机视为阻抗型负荷加入潮流程序,得到风力发电机的电磁功率,另外由风速等信息计算出风机的机械功率,根据两个功率之差值修正转差,反复迭代,最终使风机功率与发电机功率相平衡。RX模型充分考虑了风力发电机的功率输出特性,属于较完善模型,但此模型的迭代过程分两步完成,总迭代次数多,收敛速度慢。

考虑到异步发电机在输出有功功率的同时还要从系统吸收一定的无功功率,其吸收的无功功率大小与转差率s和节点电压U的大小密切相关,为减少网络损耗,一般采取无功功率就地补偿的原则,通常做法是在风力发电机组安装并联电容器组[8]。简化等效电路见图3。其中:xm为励磁电抗,xs为定子漏抗,xr为转子漏抗,xc为机端并联电容器电抗,rr为转子电阻,s为转差,定子电阻忽略。

从图3可以推得:

图3 异步发电机的简化模型Fig.3 Simplified model of asynchronousmachine

对风场而言,输出的有功功率P由风速决定,在潮流计算中可认为是给定值,此时吸收的无功功率Q与机端电压Us和转差s有关,而Us和s的关系由式(3)决定,于是可推出异步风力发电机吸收的Q与Us的函数关系式[3]:

由此可知,异步发电机节点类型具有如下特点:发出的有功功率是确定值,而无功功率则与机端电压有关。这与电压静特性负荷节点相似,因此在潮流计算中称这种电源节点为电压静特性节点,即:P恒定,U不定,Q受P、U限定的P-Q(V)。潮流计算处理此类节点时,每次迭代后都会对电压进行修正,并根据修正后的电压幅值计算出异步发电机吸收的无功功率。因此,在下一次迭代前,可把P-Q(V)节点转换成传统潮流算法能处理的PQ节点,其中P为异步发电机输出的有功功率,Q为发电机吸收无功功率与补偿无功功率的差值。该方法有较好的准确性,并且计算量较小,速度快,对现有程序改动量小。

2.2 双馈电机并网

双馈风力发电机稳态等效电路如图4。其中,xm为励磁电抗,xs为定子漏电抗,xr为转子漏电抗,rs为定子电阻,rm为励磁电阻,rr为转子电阻。

图4 双馈异步发电机稳态等效电路Fig.4 Steady state equivalent circuit of doubly-fed inductionmachine

当风速已知时,可通过风速功率特性求得该风速下发电机注入系统的总有功功率Pe。Pe由两部分组成,一部分是由定子绕组发出的有功功率Ps,另一部分是转子绕组发出或吸收的有功功率Pr。当转速高于同步转速时,转子绕组发出有功功率;当转速低于同步转速时,转子绕组吸收有功功率。双馈异步发电机的无功功率也是由两部分组成,一部分是发电机定子侧发出或吸收的无功功率,另一部分是变流器在发电机转子侧发出或吸收的无功功率。双馈机可采用恒功率因数控制运行方式或者恒电压运行方式。

由双馈风电机的等效电路,在忽略定子绕组电阻的情况下,转子绕组上发出的功率可表示为[9]

其中x=xr+xs,Us=|﹒Us|。

风电机组注入系统的有功功率为

其中,转差s可通过双馈风电机组的转速控制规律求取,双馈异步发电机的转子转速控制规律是指风电机转速与风力机的机械功率的对应关系,通常采用的转速控制规律如式(8),控制曲线如图5所示。AB段风速低于启动风速,转速维持在最低转速;BD段风速处于启动风速与额定风速之间,分两段运行,BC段进行最大功率跟踪,CD段以恒转速方式运行在额定转速;DE段高于额定风速,以恒功率方式运行在额定功率。

双馈异步风力发电机一般采用恒功率因数控制方式,设功率因数为cosφ,则Qs=Pstanφ。又由于变流器传递的有功功率较小,由变流器吸收或发出的无功很小,因此可近似为风电机组的无功功率就等于定子绕组的无功功率,即:

由式(6)和(7)可以得到:

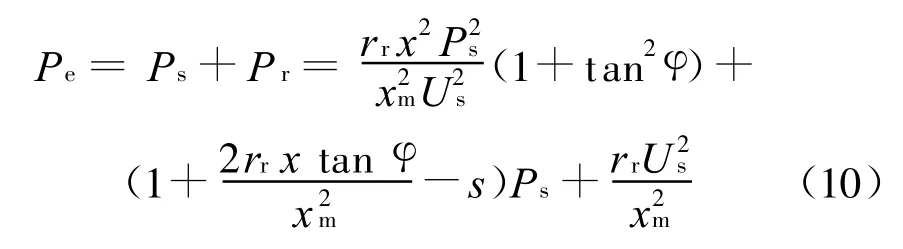
由于=tanφ,因此可知在恒功率因数控制下,当双馈风力发电机的有功功率、功率因数和转差确定时,无功功率仅是机端电压的函数。一般给定风速和功率因数,则发电机的有功功率已知,转差可由转速控制规律求取,进而可求得无功功率。

当采用恒电压运行方式时,风场节点可作为PV节点进行潮流计算,但由于定子侧无功功率受到定子绕组、转子绕组和变流器最大电流的限制,因此需要考虑各种限制条件。

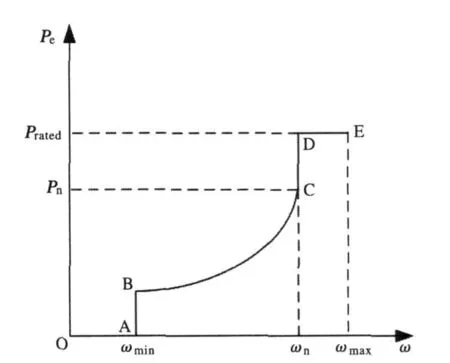
图5 双馈电机转子转速控制规律Fig.5 Rotor speed control rules of doubly-fed induction machine

3 燃料电池与光伏电池并网系统[8]

并网的燃料电池发电站一般由燃料电池、功率调节单元及升压变压器等组成,其中功率调节单元主要由逆变器、电压控制环节和功率控制环节组成,并网燃料电池发电站常见等效电路见图6,其中逆变器采用PWM,通过控制参数m和φ实现。

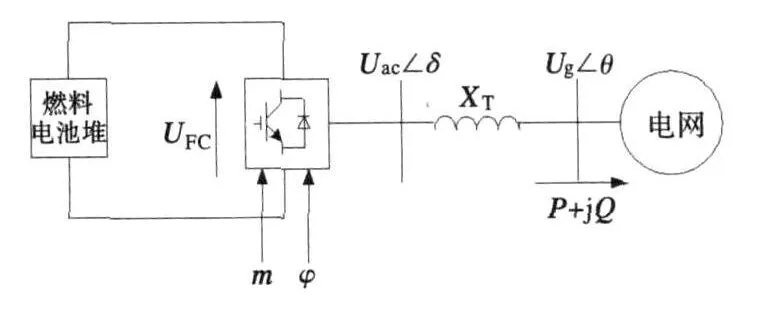
图6 燃料电池并网系统等效模型Fig.6 Equivalentmodel of gird-connected fuel cell system

由此可计算得到有功功率与无功功率:

由上式可知,燃料电池发电站的有功功率和无功功率控制通过控制参数φ和m实现。换流器的超前角φ可由燃料流量控制,通过对燃料流量控制实现对燃料电池有功输出功率的控制,这与常规发电机通过调节气门/导水叶开度实现有功调节原理类似;而对无功功率控制则是通过调整换流器的调节系数m实现,这与常规发电机调节励磁电流来控制其无功输出原理相似。因而,在潮流计算中,燃料电池发电站并网节点可作为PV节点处理。

光伏发电系统与燃料电池发电系统具有类似的并网结构,其逆变器控制原理也相似,如图7所示。其中UPV为光伏电池板的输出直流电压。

图7 光伏电池并网系统等效模型Fig.7 Equivalentmodel of gird-connected photovoltaic system

因此在潮流计算中,光伏电池发电系统可看作PV节点处理,燃料电池与光伏电池发电站正常运行时不需要从系统吸收无功,无功下限值可取0。若并网节点的无功越限,可以将该节点作为PQ节点处理,此时的无功注入为无功输出的上限或下限值。

4 结语

本文介绍了几种分布式电源典型的并网接口,针对微型燃气轮机并网系统,风力发电系统,燃料电池及光伏并网系统,分析了其并网结构及运行方式,建立了各自在潮流计算中的数学模型。根据各分布式电源的控制特性,将其节点类型归结为PV节点,PQ节点,Vθ节点,PI节点,P-Q(V)节点。针对特殊节点提出了在潮流计算中的处理方法,其本质是在迭代步将各类节点转换成为传统方法能够处理的PQ节点或PV节点,有利于开展含有分布式电源的配电系统潮流计算研究。

[1] 王志群,朱守真,周双喜,等(W ang Zhiqun,Zhu Shouzhen,Zhou Shuangxi,et al).分布式发电接入位置和注入容量限制的研究(Study on location and penetration of distributed generations)[J].电力系统及其自动化学报(Proceeding o f the CSU-EPSA),2005,17(1):54-58.

[2] 崔晓丹,于继来(Cui Xiaodan,Yu Jilai).配电网交直流同线馈送方式的潮流分析(Pow er flow ana lysis of AC and DC transm itting simu ltaneously along the same feeder line in distribution network)[J].电力系统及其自动化学报(Proceeding of the CSU-EPSA),2006,18(6):59-63,69.

[3] 王守相,黄丽娟,王成山,等(W ang Shouxiang,Huang Lijuan,Wang Chengshan,eta l).分布式发电系统的不平衡三相潮流计算(Unbalanced three-phase pow er flow calcu lation for distributed power generation system)[J].电力自动化设备(Electric Power Automation Equipment),2007,27(8):11-15.

[4] 王守相,江兴月,王成山(Wang Shouxiang,Jiang Xingyue,W ang Chengshan).含风力发电机组的配电网潮流计算(Pow er f low analysis of distribution network containing w ind power generators)[J].电网技术(Pow er System Technology),2006,30(21):42-45,61.

[5] Xiaoguang Yang.Unbalanced Power Converter Modeling for AC/DC Pow er Distribution[D].Philadelphia,USA:Co llege of Engineering,Drexel University,2006.

[6] Papadopou los M,M alatestas P,Hatziargy riou N.Simu lation and analysis o f small and medium size power systems containing wind turbines[J].IEEE T rans on Pow er Systems,1991,6(4):1453-1458.

[7] Feijoo Andres E,Cid ras Jose.M odeling of wind farms in the load flow analysis[J].IEEE Trans on Pow er Systems,2000,15(1):110-115.

[8] 陈海焱,陈金富,段献忠(Chen Haiyan,Chen Jinfu,Duan Xianzhong).分布式电源的配电网潮流计算(Study on power flow calcu lation of distribution system w ith DGs)[J].电力系统自动化(Automation of Electric Pow er Systems),2006,30(1):35-40.

[9] 申洪(Shen H ong).变速恒频风电机组并网运行模型研究及其应用(Studies on Integrated Variab le-Speed Constant-Frequency W ind Turbine Models and the Application)[D].北京:中国电力科学研究院(Beijing:China Electric Power Research Institute),2003.