马尔科夫链在电力负荷组合预测中的应用*
李 敏,江 辉,黄银华,宋小明
(湖南大学电气与信息工程学院,长沙 410082)
电力负荷预测是电力系统安全、经济运行的前提,是实现电网增容和改建的重要依据。负荷预测的准确性直接影响新机组的装机容量、安装位置和安装时间。因此,高精确度的负荷预测是电网规划的重要内容。
电力负荷预测受政策、经济、环境等因素影响,是典型的复杂非线性问题。在多因素影响下,单一负荷预测很难准确描述电力负荷变化规律[1~3]。为合理考虑多种因素对电力负荷影响,文献[4~6]提出组合预测模型。组合预测整体上优于单个预测,同时组合预测中变权重方法比固定权重更符合实际,预测结果更准确。但难点在于如何分配各种方法的权重。常见的权重处理方法[7]有最优组合和变权组合。最优组合预测可能出现没意义的负权重,且权重可能不是最优;而变权重克服了最优组合的缺点,更加符合实际。但确定方法较复杂。
本文利用马尔科夫链对筛选后各方法的状态概率分布的变化规律进行拟合,将一步转移概率矩阵的估计问题转化为多元约束的自回归模型,进而求解出一步转移概率矩阵的最小二乘公式解。然后利用一步转移概率矩阵的估计和初始状态概率分布给出各方法的权重,并利用非负权重进行组合预测。仿真实例验证了本方法的可行性和优越性。
1 马尔科夫链基本原理
马尔科夫[8,9]过程是具有无后效性的随机过程。无后效性是指在已知“现在”的条件下,“将来”的状态与“过去”的状态无直接关系。时间和状态都离散的马尔科夫过程,为马尔科夫链。
对离散空间E中的随机序列{Xt,t=1,2,…},若对于任意的非负整数n,l,k及任意的非负整数及满足:

则随机序列{Xt,t=1,2,…}为马尔科夫链。
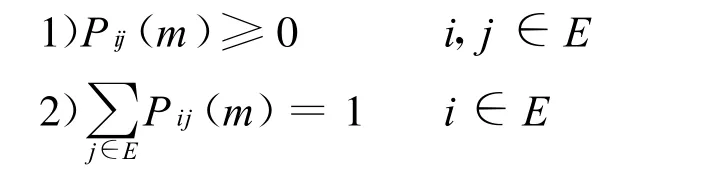
2 基于马尔科夫链的组合预测
设yt为t时刻负荷观测值(1≤t≤T)或预测真值(t>T)(t=1,2,…),T为拟合时段,t=T+1,…为预测时段。假令有N种负荷预测方法,第i个预测方法对t时刻变量yt的拟合值(1≤t≤T)或预测值(t>T)记为yti。当将yt看做是随机变量时,yt1,yt2,…,ytN可将yt取值分为N个状态,设:

特别当
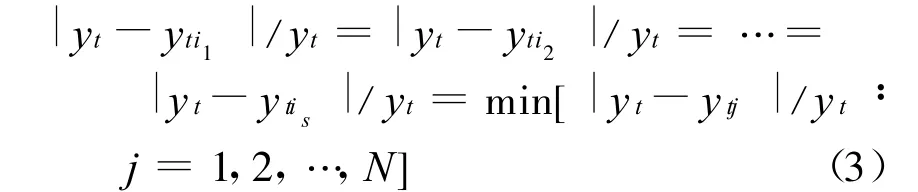
时,i={i1,i2,…,is};其中下标s(s≥1)表示满足|yt-yti|/yt=min[|yt-ytj|/yt∶j=1,2,…,N]时的预测方法数。
用马尔科夫链拟合随机序列{X t∶t=1,2,…},状态概率

则状态概率分布为P t=[Pt1,Pt2,…,PtN]′。记P ti的估计值为,则:

由此产生状态概率分布的观测值
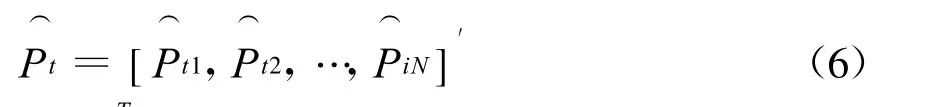
设随机序列{Xt∶t=1,2,…}的一步转移概率矩阵为Q=[qij]N×N,设
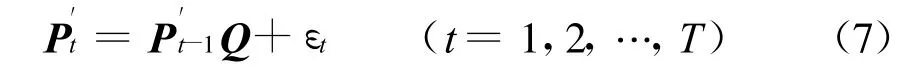
其中ε1,ε2,…,εT为随机误差向量。注意到Q应满足b′Q′=b′,其中b′=(1,1,…,1)为一个N维行向量,则Q的估计问题化为如下约束多元自回归模型对Q的估计问题

对于上式,可以证得[10]:若C′C可逆,则矩阵Q的最小二乘解为
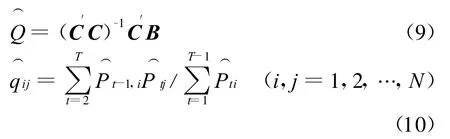
E(ε′)的估计为

这样可得状态概率的预测公式为

3 多模型的自动筛选方法
负荷预测的数学模型都是理想抽象的。由于预测量发展变化规律的多样性和复杂性,以及许多不确定因素的存在,单一预测模型的精度不可能在所有情况下都有较高的预测精度。因此,在进行组合预测之前,应对众多单一预测模型进行判断和筛选,舍弃那些效果明显较差的模型,同时选出比较有效地模型,从而进一步提高组合预测的精度。
本文采用一种多模型自动筛选算法[11]对单一预测模型判断筛选。该算法利用决策理论中的几率矩阵(odds-matrix)来定量确定每种单一模型的权重,每种权重代表该方法的优劣性,通过权重概率分布函数判断各预测模型的显著性,从而筛选出符合特定地区、特定时期负荷特点的预测方法。
假设e种单一预测模型实际的优劣性用权重相量w={w1,w2,…,we}表示,权重越大,预测模型i越好。令O exe为决策矩阵,矩阵中的每一个元素Qij可以看作预测模型i优于j的几率,则自动筛选算法可分为以下2个步骤:
1)应用决策理论中的odds-matrix方法评价各个单一方法,引入权重概率分布函数来描述各个方法的优劣性。根据每个单一预测模型的原始误差,生成决策矩阵,获取决策矩阵Oexe,并利用最小二乘法或特征向量法等方法求取权重相量w。
2)估计分布函数的数学期望,得到优越方法的集合。根据权重相量w及权重的数学期望EV对单一预测模型进行判断筛选。当权重w i>EV时,则预测方法参与组合预测,否则剔除该方法。
基于马尔科夫链拟合的变权重组合预测的流程图如图1所示。
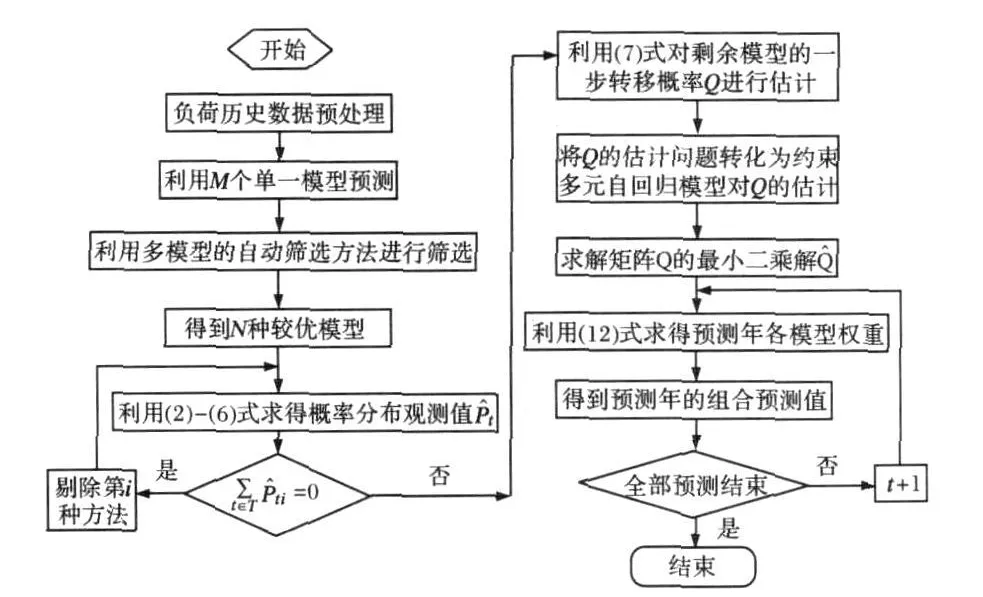
图1 计算流程Fig.1 Flow chart of calcu lation
4 算例分析
采用文献[12]中算例所提供的数据,将某地区1998~2005年全社会用电量作为样本(见表1),利用1998~2002年数据,采用本文所提组合预测方法对2003~2005年该地区全社会用电量进行预测。

表1 1998-2005年用电量数据Tab.1 Electric energy consum ption from 1998 to2005
利用指数模型I、抛物线模型、灰色系统法、3次曲线模型、人工神经网络、指数平滑法、模糊聚类识别预测法7个单一模型预测。根据单一模型预测结果,利用本文多模型自动筛选方法筛选,从中筛选出抛物线模型、3次曲线模型、灰色系统法3种单一模型。运用本文组合预测方法对2003~2005年该地区全社会用电量进行组合预测,得出3个模型权重值和组合预测值。表2为筛选出的三种方法负荷预测结果;表3为组合预测权重值和预测结果。

表2 3种模型的预测结果Tab.2 Results of three forecastingmodels
表4为本文预测方法和文献[12]预测方法比较。由表4知,本文方法最小误差为0.09%、最大误差为0.25%,而文献[12]预测方法的最小误差为0.17%、最大误差为0.8%。可见,本文预测方法较精确,在历史数据与预测年越接近时预测越准确,2003年时,本方法误差仅为0.09%。
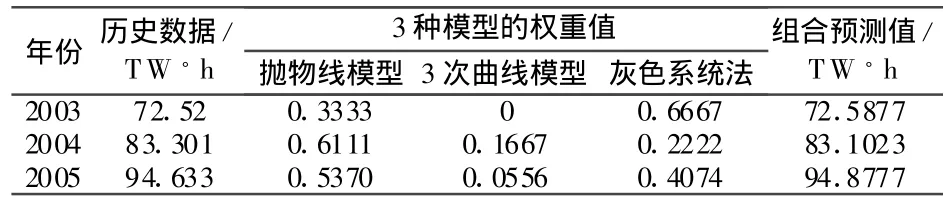
表3 3种模型时变权重及组合预测结果Tab.3 Resu lts and weights of threemodels

表4 预测结果比较Tab.4 Comparison o f the forecasting resu lts
5 结语
本文以最小误差为准则,利用马尔科夫链拟合状态概率分布的变化规律,并将一步转移概率矩阵的估计问题转化为多元约束自回归模型,然后利用一步转移概率阵的估计和初始状态概率分布给出了状态分布的变权重预测方法。实例表明,该方法推理简单,不会出现负权重,具有实用性;同时,计算中还发现:所用历史资料与待测预测年时间上越接近,则预测越准确。
[1] 李翔,高山,陈昊(Li Xiang,Gao Shan,Chen Hao).基于变结构协整理论的中长期电力负荷预测模型(A new medium-and long-term forecastingmodelbased on variab le structu re cointeg ration theory)[J].电网技术(Power System Technology),2007,31(9):48-52.
[2] 雷绍兰,孙才新,周湶,等(Lei Shaolan,Sun Caixin,Zhou Quan,et a l).基于径向基神经网络和自适应神经模糊系统的电力短期负荷预测方法(Shortterm load forecasting method based on RBF neural network and ANFIS system)[J].中国电机工程学报(Proceedings o f the CSEE),2005,25(22):78-82.
[3] 陈泽淮,张尧,武志刚(Chen Zehuai,Zhang Yao,Wu Zhigang).RBF神经网络在中长期负荷预测中的应用(Ap plication of RBF neural network in medium and long term load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2006,18(1):15-19.
[4] 肖先勇,葛嘉,何德胜(Xiao Xianyong,Ge Jia,He Desheng).基于支持向量机的中长期电力负荷组合预测(Combination method of m id-long term load forecasting based on support vec tor machine)[J].电力系统及其自动化学报(Proceedings of the CSUEPSA),2008,20(1):84-88.
[5] 李春生,王耀南(Li Chunsheng,Wang Yaonan).基于条件熵的电力负荷组合预测模型(Combinationmodel of load forecasting based on conditionalentropy)[J].电力系统及其自动化学报(Proceedings o f the CSUEPSA),2007,19(4):55-58.
[6] 游仕洪,程浩忠,谢宏,等(You Shihong,Cheng H aozhong,Xie Hong,et a l).模糊组合预测在中长期负荷预测中的应用(Application of combination forecasting by fuzzymethod in m id-and long-term load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2004,16(3):53-56,78.
[7] 余健明,燕飞,杨文宇,等(Yu Jianm ing,Yan Fei,Yang Wenyu,eta l).中长期电力负荷的变权重组合预测模型(G ray variab le w eight combination model for m iddle and long term load forecasting)[J].电网技术(Pow er System Technology),2005,29(17):56-60.
[8] 吴凯,林争辉(W u Kai,Lin Zhenghui).马氏链在集成电路功耗估计中的应用(Application o f Markov chain in VLSIpower estimation)[J].计算机工程(Computer Engineering),2003,29(13):162-164.
[9] 何鑫,宋平岗,官二勇(He Xin,Song Pinggang,Guan Eryong).用马氏链方法预测全国年发电量趋势(Forecasting the trend of electricity p roduction in the year future by using Markov chain)[J].华东交通大学学报(Journal of East China Jiaotong University),2006,23(4):51-54.
[10]张尧庭,方开泰.多元统计分析[M].北京:科学出版社,1982.
[11]高峰,康重庆,夏清,等(Gao Feng,Kang Chongqing,Xia Qing,et a l).负荷预测中多模型的自动筛选方法(Multi-model automatic sifting methodology in load forecasting)[J].电力系统自动化(Automation of Electric Power System s),2004,28(6):11-13,40.
[12]孙广强,姚建刚,谢宇翔,等(Sun Guangqiang,Yao Jiangang,X ie Yuxiang,et al).基于新鲜度函数和预测有效度的模糊自适应变权重中长期电力负荷组合预测(Com bination fo recast of medium-and long-term load using fuzzy adaptive variab le weight based on fresh degree fun ction and forecasting availability)[J].电网技术(Power System Technology),2009,33(9):103-107.

