A－SMGCS机场场面运行控制的Petri网建模＊

朱新平 韩松臣 汤新民

（南京航空航天大学民航学院 南京 210016）

先进机场场面引导与控制系统（A－SMGCS），属于飞行区场面运行的一种精细化控制手段，其特点是能在各种气象条件、交通密度和场面布局下，利用多种传感技术获取活动目标的位置信息，并实时进行冲突探测与解脱.多年来，国内外关于场面运行建模多局限于传统运筹学基础上的生产调度与控制方法［1－3］，存在可解决问题规模较小，实时性差等缺点，且直接以A－SMGCS运行控制为目标的研究成果较少.文献［4－5］综合考虑航空器场面运行和管制员决策行为，采用着色Petri网对场面管制过程进行建模.文献［6］以航班进离港及地面作业保障为研究对象，分别建立了对应的带抑制弧高级Petri网模型，以及面向对象的时序Petri网模型.文献［7］采用着色Petri网对场面管制的动态变化过程进行建模.文献［8］采用开放Petri网对空中交通管制辅助决策系统进行建模，能够有效地描述管制系统与外部控制的交互机制.文献［9］采用普通Petri网建模航空器场面运行过程，依据管制规则和运行约束定义模型的标识控制规范，并基于有限容量库所设计结构型Petri网控制器.本文采用自顶向下和模块化的建模方式，实现A－SMGCS场面运行控制的Petri网建模.建模过程分两步，即先建立场面资源模型，然后结合航空器场面滑行模型，生成最终的场面运行控制Petri网模型.

1 场面运行控制建模要求

A－SMGCS场面运行过程涉及多种资源（如跑道、滑行道、停机坪／机位等），加之航空器对上述资源的并行动态占有，使得整个场面运行过程规模庞大，具有多约束、多目标和随机不确定性.另一个主要特点是场面资源布局复杂.如果从更高层去抽象，场面运行过程则可看作是由一连串的离散事件（如引导灯关闭或开启，管制放行等）分开的航空器滑行过程组成的离散事件动态系统（DEDS）.因此，A－SMGCS场面运行过程建模需要考虑场面资源特定的物理布局，全面考虑并抽象出涉及的各种资源，及其与航空器之间的复杂交互关系.

2 场面资源基本网模型

2.1 基本网模型定义与生成规则

定义1 场面资源基本网模型定义为N＝｛P，T，I，O，M｝.其中，库所集合P 为各典型运行单元，包括跑道、滑行道交叉口和直线段、停机位运行单元；T为所有变迁的集合，表示航空器穿越运行单元边界活动；任意变迁t∈T具有惟一的输入或输出库所，表示航空器只能从一个单元离开然后进入另一个单元；M为模型标识，表示场面运行状态.

定义2 运行单元有向图定义为G＝（E，R）.其中：E为顶点集合；R是边集合.G中顶点对应于离散得到的各典型运行单元（包括交叉口、直线段、跑道、停机位），可表示为E＝｛e1，e2，…，en｝，n为运行单元总数；对e1，e2∈E，若从e1到e2存在有向边连接，则表示从运行单元e1到e2存在可供航空器滑行的通道.对运行单元有向图G采用联接矩阵表示法，图的联接矩阵与图一一对应.

由有向图G生成基本网模型N 的规则：（1）建立从G的顶点集E到N的库所集P的一一映射f，即P＝f（E）；（2）对任一cij而言，若cij＝1，则在库所pi，pj∈P 之间添加变迁tij，使得pi∈（p）tij，pj∈t（p）ij，并将tij加入集合T中；（3）若某一航空器a的坐标（xa，ya）位于运行单元ei范围内，则该单元对应库所标识M（pi）＝1；将M（p），p∈P按照与E对应的顺序排成行向量M＝［M（p1），M（p2），…］，便得到基本网模型的标识.

2.2 基本网模型的扩展

场面资源具有固定数量的典型运行单元（如交叉口、直线段、停机坪／机位等），因此可基于模块化和“自顶向下”的建模思想，将各典型运行单元划进一步分为小的活动区间，构建对应的精细化模块，并将基本网模型中的库所用其对应的精细化模块替代，得到能描述更多运行细节的场面模型.下面给出各单元精细化模块的构建思路，以及此模块替代基本网中库所的替代规则.

2.2.1 典型运行单元精细化模块

定义3 交叉口Petri网模型 定义为S＝｛P，T，I，O，C，B，M｝.其中P＝｛ps｝（s为交叉口编号），库所ps为交叉口单元划分的活动区间；T＝TI∪TO为航空器活动，其中TI（TO）分别为航空器进入（离开）交叉口活动；将可由停止排灯控制的交叉口活动用可控变迁表示，对应变迁t有控制库所c∈C 满足c∈（c）t；I（O）为模型的输入（输出）函数；B⊆（C×T）；M 为模型标识，表示交叉口的占用情况.

变迁集合T＝TI∪TO描述了交叉口模块与其他模块的联系，称为模块对应的全局变迁集合.

例1 以图1a）所示一类典型的交叉口运行单元为例.假设该交叉口所连每个直线路段均允许各类航空器分时双向运行，也即在不同的时段内允许各类航空器沿某一方向滑行，根据定义3可得其对应的Petri网模型如图1b）所示.变迁t0，t1对应的位置有单向停止排灯，由于只对进入交叉口起控制作用，因此，仅需为变迁t1添加控制库所.变迁t2，t3对应的位置有双向停止排灯，对进出交叉口均起控制作用，因此，需为对应的变迁t2，t3均添加控制库所.

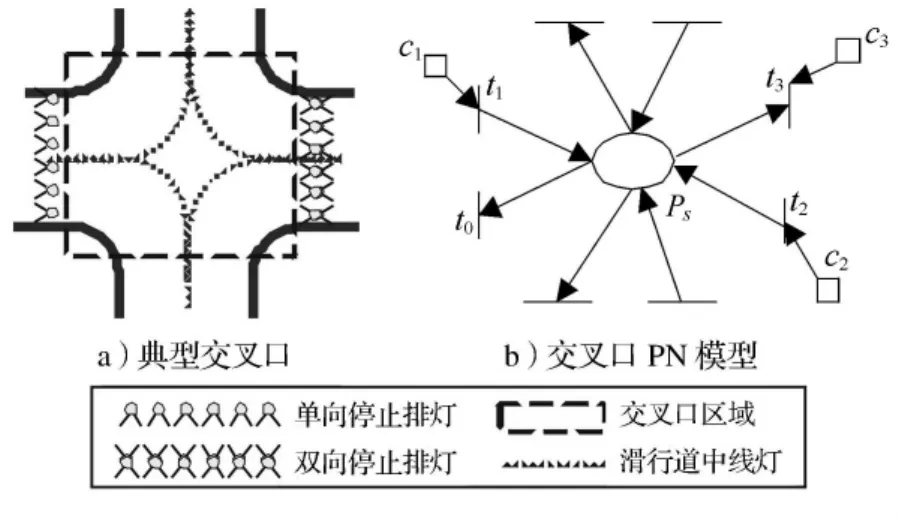
图1 滑行道交叉口模块及其Petri网模型

定义4 直线段Petri网模型 定义为L＝｛P′，T′，I′，O′，C′，B′，M′｝.其中，P′＝｛pm｝，pm为直线段单元划分的活动区间；变迁集合T′＝TV∪表示航空器直线段活动，且tm，n∈TV（m，n为直线段活动区间编号）表示航空器穿越直线段上划分的活动区间，t∈表示航空器进入或离开直线段；将可由停止排灯控制的直线段活动用可控变迁表示，对应变迁t有控制库所c∈C满足c∈（c）t；其他概念同定义3.

例2 以图2a）所示直线段运行单元为例，假设该直线路段允许各类航空器分时双向运行，根据定义4可得其对应的Petri网模型如图2b）所示.

定义5 跑道Petri网模型 定义为S＝｛P″，T″，I″，O″，C″，B″，M″｝.其中 P″＝｛pr｝，库所pr表示跑道运行单元；T″＝TI∪TO，变迁集合TI和TO分别表示航空器进入和脱离跑道活动.∀t∈TI均为可控变迁，有控制库所c∈C使得c∈（c）t；t∈TO为不可控变迁；其他概念同定义3.

例3 以图3a）所示跑道活动单元为例，根据定义5可得其对应的Petri网模型如图3b）所示.

图2 滑行道直线段模块及其Petri网模型

图3 跑道模块及其Petri网模型

定义6 停机位Petri网模型 定义为A＝｛P‴，T‴，I‴，O‴，C‴，B‴，M‴｝.其中 P″＝｛ph｝∪｝（h为停机位编号），库所ph表示机位活动区域，表示进出该机位的机坪滑行线交叉口；T‴＝TA∪TU为航空器机位活动变迁，其中变迁t∈TU表示航空器进入或离开机位交叉口，t′∈TA表示航空器进入或离开机位且为可控变迁，有控制库所c∈C满足c∈（c）t′，其他概念同定义3.

TU描述了模块与外界的交互，称为模块的全局变迁集合，TA为模块的局部变迁集合.

例4 典型的机位运行单元如图4a）所示，包括进出机位交叉口和机位活动区域，根据定义6可得其对应的Petri网模型如图4b）所示.

图4 机坪停机位模块及其Petri网模型

2.2.2 基本网模型的替代规则 记上节各单元精细化模块为 WP＝｛Pk，Tk，Ik，Ok，Ck，Bk，Mk｝，将基本网N＝｛P，T，I，O，M｝中的库所用对应的WP替代，可得到更能描述运行细节的场面模型，记为 Nt＝｛Pt，Tt，It，Ot，Ct，Bt，Mt｝，称之为场面资源精细化Petri网模型.其中：（1）Pt＝∪Pk，Tt＝（∪）∪T（其中为各替代模块的局部变迁集合）；（2）对∀p∈Pt，∀t∈Tt，It（p，t）＝Ik（p，t），Ot（p，t）＝Ok（p，t）；（3）若t∈Tt在其对应的模型中满足（c）t＝｛c｝，则有（c，t）⊆Bt，且c∈Ct；（4）对∀p∈Pt，Mt（p）＝Mk（pi），其中pk∈Pk.

上述规则中，规则（1）将基本网模型中的每一个库所都用对应的精细化模块替代，并将基本网中的变迁进行扩展，增加了各模块中所包含的局部变迁；规则（2）中Nt中输入和输出函数均来自各精细化模块的输入输出函数；规则（3）中添加精细化模块的控制库所及其连接关系；规则（4）对场面精细化模型中的标识（也即航空器运行状态）依据精细化模块来确定.

3 航空器建模和场面最终模型

用着色托肯建模每一架航空器a∈A，其颜色为＜rr（a）＞.其中，rr（a）表示该航空器从当前位置开始的后续滑行路径（用库所序列表示）.如M（ps）＝＜rr（a）＞表明航空器当前处于ps对应运行区间，托肯颜色rr（a）代表航空器a从ps开始将会通过的运行区间，由此则可描述此航空器的运行趋势.

定义航空器场面滑行计划集合为W＝｛π1，…，πh｝，其中πi＝rr（a）为航空器的后续滑行路径.将资源精细化模型Nt与W 相结合，可得到场面运行最终模型：

其中，相关元素的确定方法如下.

1）着色属性ζ可由算法Computζ（Nt，W）确定.

2）对∀（pi，TIm）∈It，（pi，Tim）＝ID，其中ID为单位函数，对托肯颜色不做任何改变；否则（pi，Tim）＝0.

3）对∀（pm，Tim）∈Ot，（pm，Tim）＝UP，其中：UP 为函数，将托肯颜色由＜rr（a）＞变为＜rr′（a）＞（rr′（a）为从rr（a）中去掉其第一个元素后的剩余库所序列；否则（pm，Tim）＝0.

4）颜色集合Ω＝｛ζ（x）｜x∈Pt∪Tt｝.

算法.Computζ（Nt，W）.

输入.Nt＝｛Pt，Nt，It，Ot，Ct，Bt，Mt｝；

W＝｛π1，…，πh｝，πi＝rr（a）.

目的.为每一个元素q∈Pt∪Tt计算其着色集合C（q）.

步骤1 对πi＝rr（a），对∀pi∈rr（a），将颜色属性πi加入到C（pi）中.

步骤2 对pi的后向变迁tim∈，将颜色属性πi加入到C（tim）中.

步骤3 对其他πi继续上述步骤.

算法复杂度分析：场面运行模型的构造过程，其主要工作在于为各元素计算着色属性.实际上，算法Computζ（Nt，W）的复杂度很低，为O（h×（｜Pt｜＋｜Tt｜）），属于多项式算法，其中h为场面运行的航空器架数，｜·｜为集合·中元素个数.

4 建模实例

以首都机场T3C航站楼东侧飞行区的一部分为例，该部分的场面资源构成如图5所示，主要资源包括机坪停机位301至312的活动区Z1至Z13，滑行道交叉口Z14至Z16，Z24至Z26，以及Z19；滑行道直线段 Z17，Z18，Z20至 Z23；跑道运行区Z27；场面停止排灯b0至b10，其中b0为双向停止排灯，其余为单向停止排灯.

图5 首都机场T3C航站楼飞行区一部分场面资源构成

利用由运行单元有向图G生成基本网模型N的规则，得到基本网模型如图6所示.其中，每个库所pj对应一个运行单元zj，且相邻库所间存在2个活动变迁，描述航空器的不同运行方向.然后根据替代规则，将基本网模型中的库所用精细化模块替代，得到场面资源精细化模型，例如可将图7基本网模型中的库所p17用对应的精细化模块替代.最后，采用着色托肯建模航空器，并得到最终运行模型.若Z17中航空器a0的滑行路径为π0＝rr（a0）＝（，p16，p15，p10），Z23中航空器a1的滑行路径为π1＝rr（a1）＝（p23，p26，p27），则模型的标识）＝＜π0＞，（p23）＝＜π1＞描述了场面运行状态，并可由算法Computζ（Nt，W）确定航空器滑行路径上各库所和变迁的着色属性如下：C（）＝｛π0｝，j＝1，2；C（pi）＝｛π0｝，i＝16，15，10；C（）＝｛π0｝；C（t17，16）＝｛π0｝；C（t16，15）＝｛π0｝；C（t15，10）＝｛π0｝；C（pi）＝｛π1｝，i＝23，26，27；C（t23，26）＝｛π1｝，C（t26，27）＝｛π1｝.在场面运行控制Petri网模型中，通过为其中的控制库所决策控制律，并进一步给出对应位置停止排灯切换指令，即可控制航空器场面滑行并避免冲突.

图6 图5所示飞行区场面运行的Petri网模型

5 结束语

提出一种基于Petri网的A－SMGCS场面运行控制建模方法.该方法有以下优点：（1）基于典型运行单元划分建立的有向图模型，从全局视角清晰、直观地反映了场面资源组成及关联；（2）采用Petri网间接建模场面运行过程，既保证了模型总体结构的清晰性，又达到了将场面复杂动态过程转换为具有精确语义的Petri网模型的目的，降低了建模过程的复杂度和调整的难度，并避免了信息描述不清、考虑不全面等原因而带来的控制软件设计周期延长；（3）引入控制库所体现了外界对场面运行过程的控制作用，可消除航空器资源占用冲突.借助于所建立的模型，可进一步对场面运行过程展开逻辑分析与控制综合研究.

［1］Visser H，Roling P.Optimal airport surface traffic planning using mixed integer linear programming［C］／／Proc.of AIAA＇s 3rd Annual Aviation Technology，Integration，and Operations（AtiO）Technology Conference.Denver，CO，2003：17－19.

［2］Capozzi B J，DiFelici J.Towards automated airport surface traffic control：potential benefits and feasibility［C］／／Proc.of AIAA Guidance，Navigation，and Control Conference and Exhibit.Providence，RI，2004：1－16.

［3］Gillian C，Arthur R，Receding Horizon.Iterative optimization of taxiway routing and runway scheduling［C］／／Proc.of AIAA Guidance，Navigation，and Control Conference.Chicago，Illinois，2009：1－14.

［4］Werther B.Colored Petri net based modeling of airport control processes［C］／／Proc.of International conference on Computational Intelligence for Modelling，Control and Automation，CIMCA.Sydney，2006：1－6.

［5］Werther B，Moehlenbrink C，Rudolph M.Colored Petri net based formal airport control model for simulation and analysis of airport control processes［J］.Lecture Notes in Computer Science 4561，2007：1 027－1 036.

［6］秦 瑛.机场终端区作业的离散事件系统建模与优化［D］.北京：中国民用航空学院空管学院，2006.

［7］Demael J J，Levis A H.On the generation of a variable structure airport surface traffic control system［C］／／Proc.Of IEEE International Symposium on Intelligent Control.Tallinn，IEEE Press，1989：74－81.

［8］黄圣国，肖 靖.基于Petri网的空中交通管制辅助决策系统［J］.南京航空航天大学学报，2000，32（4）：206－211.

［9］Tang Xinmin，Zhu Xinping，Han Songchen.Petri net controller synthesis for advanced surface movement guidance and control system ［C］／／Proc.of IEEE International conference on Information and Automation.USA：IEEE Press，2009：483－488.