超大型海船弯曲航段所需航宽研究

徐新中 张玉峰 刘明俊 徐言民

（江阴海事局1） 江阴 214431） （江阴兴澄特种钢铁有限公司2） 江阴 214431）（武汉理工大学航运学院3） 武汉 430063）

目前我国每年进口矿石达14 800万t（2003年），矿石来源主要为澳大利亚（占40.2%）、巴西（占28.3%）、印度（占22.3%）、南非（占6.6%），另有2.5%来自其他国家.长江下游矿石运输主要采用二程运输方式.一程远洋运输以15万～20万DWT的船型为主.二程运输通常有2种方式，一种是远洋运输大型船在外海码头完全中转卸载后，用3万～5万DWT二程船转运至长江下游水域的运输方式，另一种远洋运输大型船在外海中转码头减载后直抵长江下游码头.比较两种运输方式，在减载量占载重量的比例不大的条件下，采用一程远洋运输大型船减载直抵长江下游码头的运输方式具有运输成本相对较低的优势，也可以适应长江下游水域发展的需要，做到合理、高效利用现有泊位资源的要求.超大型海船减载进出福姜沙水道后可以将大型海船进江里程大大延伸，对江阴的经济将具有巨大的拉动作用，对江阴兴澄特钢的可持续发展和积极应对金融危机具有积极意义.

目前15万t海船可以直抵江阴福姜沙水道下游的砂钢码头，但由于福姜沙水道曲折多弯，而且流压角较大，航行条件比较复杂.有必要对超大型海船弯曲航段通航宽度进行研究，以验证超大型海船航经福姜沙水道的可能性.刘明俊等［1－5］曾分别对船舶风致漂移、流致漂移和过弯道航宽进行了研究.本文将风致漂移、流致漂移模型引入船舶过弯所需航宽模型，并进行了实例计算.

1 船舶弯曲航道通航宽度建模

1.1 弯道横流角

横流角β是指横流方向与航道轴线的夹角，该值的大小决定了横流对船舶过弯时的作用方向和大小.设某弯道凸岸和凹岸航道边线的曲率半径为R1和R2.弯道航宽示意图见图1.

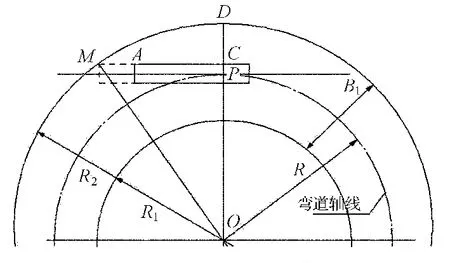
图1 弯道航宽示意图

对于某一具体弯道而言，流向角β值变化不大，若图中轴线的曲率半径为R，河宽为B，则有

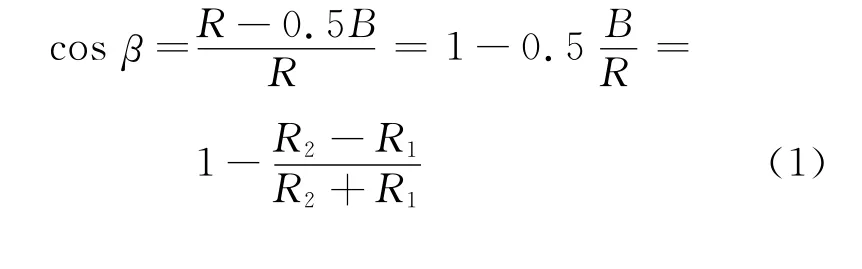
1.2 坐标系

为便于计算船舶通过时所需要的航道宽度，首先建立计算坐标.设定坐标的原点均位于各航段的轴线上，纵轴Y平行于航道轴线指向下游，横轴X垂直于各自航道轴线指向右岸.船舶航行时，设船首尾线与Y轴的夹角称为偏航角α，流向与Y轴的夹角称为流向角β，风作用方向与Y轴的夹角称为风向角αf，如图2所示.

图2 计算坐标示意图

1.3 弯曲航段过弯运动数学建模

首先确定代表船舶在无风作用下通过弯曲河段所需航宽B1、受风作用产生的风致漂移量ΔBf，然后根据叠加原理建立代表船舶过弯时，在有风、流作用情况下所需的航道宽度.

1）无风流影响下所需航宽 船舶在无风流作用情况下，通过弯曲航段所占航宽（B1）的大小可用下式计算

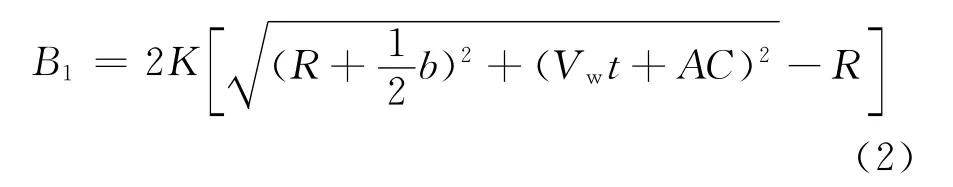
式中：K为系数，按四六分心挂高，取1.25；R为航道轴线曲率半径，m；b为船舶宽度，m；AC为船舶转心至船尾的距离，m，由转心位置确定，根据船舶操纵理论转心位置一般位于船舶重心前1／5～1／3L，取AC＝3／4L，其中：L 为船舶长度，m；Vw为过弯时的航速，m／s；t为船舶对舵的响应时间，s，根据代表船型B船的实船旋回试验结果选取，计算时取28s.

2）流致漂移量 代表船舶通过弯道时，在流的作用下产生的横向漂移量，可用下式计算

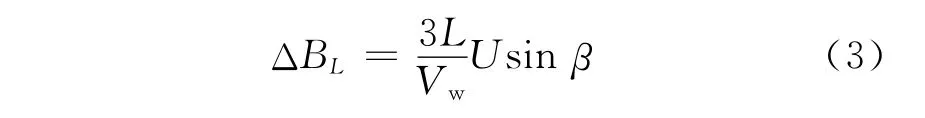
式中：U为流速.

3）风致漂移量

式中：K′为修正系数，取0.038～0.041；Ba为船体水线上侧受风面积，m2；Bw为船体水线下侧面积，m2；Bw＝Ld，d为船舶吃水，m；Vs为风中船速，kn；Va为相对风速，m／s；αf为风向与航道法线的夹角，（°）.

4）所需航宽

2 弯曲航段所需航宽计算实例

2.1 航道描述

以江阴福姜沙水道为例进行计算.水道航道概况见图3～4所示，基本参数如表1所列.

图3 福北FB＃5～FB＃7（弯曲段）

图4 福南FB＃47（弯曲段）

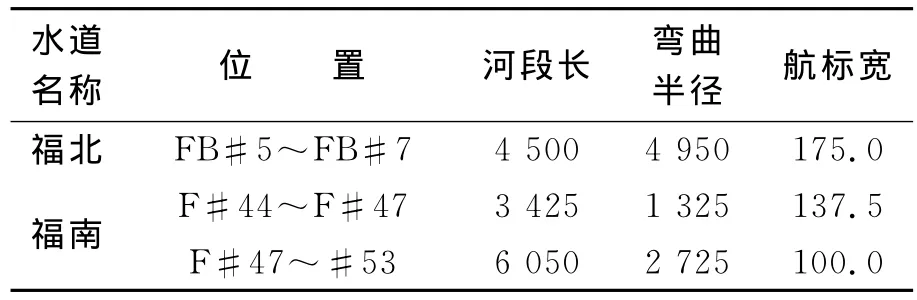
表1 江阴姜沙水道尺度 m

由表1可见，福北水道相对福南水道而言航行条件较优越，航道基本顺直，但航道宽度不大，其中FB＃5～FB＃7航道呈弯曲状，是代表船舶安全通过该水道的主要碍航因素.在该水道航标标示的可航水域范围内，顺直段最窄处在FB＃4～FB＃5之间约650m长的航段，航宽175m；弯曲段（FB＃5～FB＃7）最窄处航宽也仅175m.

福南水道下端出现呈S形的2个连续反向的急弯，航道不仅弯曲狭窄，且码头密布，船舶流量大，是代表船舶安全通过该水道的主要碍航因素.航标标示的可航水域范围内，2个反向弯道的最窄处航宽分别为137.5m和100m.

按照最不利的原则，代表船舶过福北水道时，如果最窄处能保证安全通过，则其他航段一般能安全航行，因此顺直段仅对福北水道航标标示水域可航宽度最窄处进行分析计算，即FB＃4～FB＃5之间约650m长的航段.

2.2 计算条件

1）流速与流向 福姜沙水道水流以落潮流为主，洪水期落潮流流速一般在1.5～1.8m／s，最大可达2.5m／s，其中顺直段流速大小按1.0，1.5和2.0m／s 3个流速级计算，顺流航行取正值，逆流航行取负值，流向角β取5°；弯曲河段流速大小仍按1.0，1.5和2.0m／s 3个流速级计算，流向角β通过式（1）求取.

2）风速与风向 计算中分别按照5，6，7等4个风级考虑，取不利横风，即风向角αf取90°.

3）航速 船舶航速分别按限制速度8，10，12 kn考虑.相关计算参数见表2.

表2 相关计算参数

4）船速 对应不同航速和流速下，船舶的顺、逆流船速计算值，见表3.

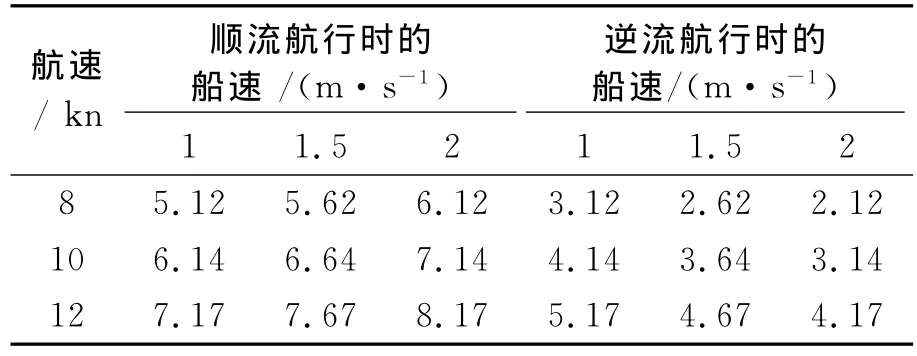
表3 船舶顺、逆流船速

2.3 计算结果

根据上述计算条件对船舶上、下行通过福姜沙水道弯曲航段的所需航宽情况进行计算，结果如表4所列.

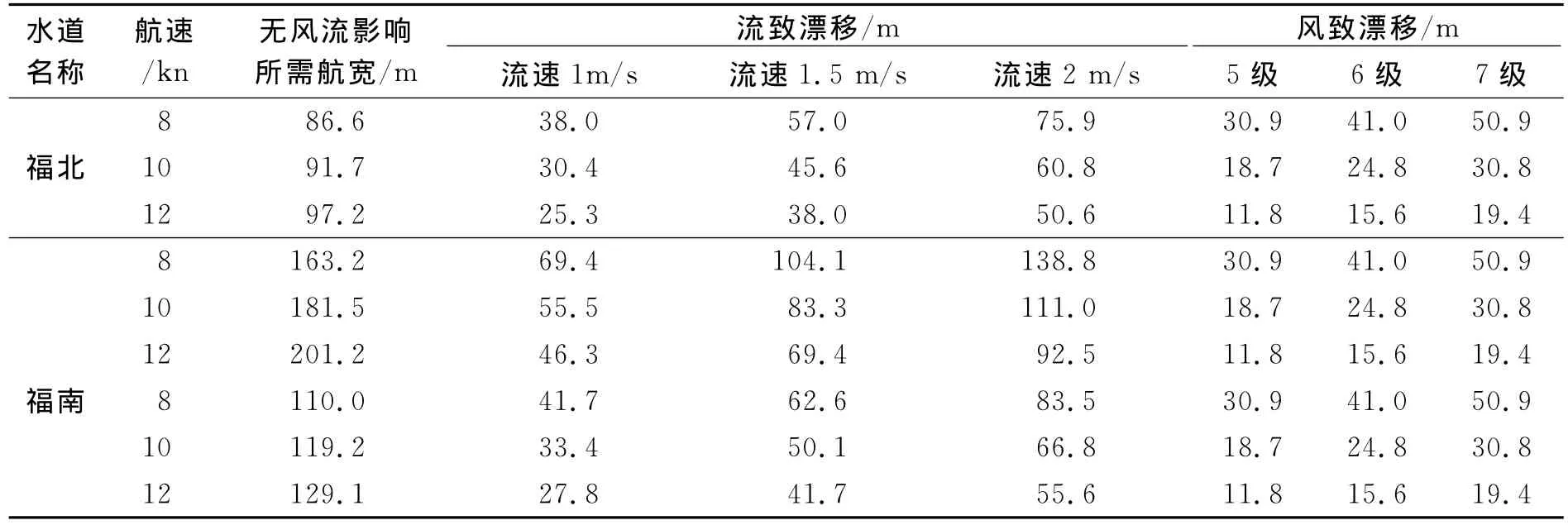
表4 通过弯道所需航宽计算表

从表5可以看出，在目前设标情况下超大型海船通过福北水道的弯曲航段，由于航标标示航宽最窄处仅约175m，遇流速较高和不利横风时航标标示的可航水域会略显不足.但福北水道弯曲段最窄处，在多年平均低潮位下的实际可航水域宽度可达363m，去掉航标绕标位旋回所需水域2×50m，则平均低潮位下最窄处至少有263 m的有效航宽，说明代表船舶通过福北水道的弯曲段时，只要合理控制航速、及时调整航向防止偏航、有效布置航标安全航行是有保障的.福南水道主要是以弯、窄碍航为主，其2个反向弯道方向变化较大.在现有航标标示的航道范围内，2个反向弯道的有效航宽分别仅为135.5，100m（扣除代表船舶航行中必须与左右侧航标保持的安全距离2×50＝100m），因此目前代表船舶安全通过福南水道，从现有航标标示的实际航宽看，不能满足代表船舶安全通航所需航宽的要求.

3 结束语

本文提出的超大型海船弯曲航段通航尺度计算模型，可以在考虑风致漂移、流致漂移和航道尺度的情况下，分析现有航道条件是否满足超大型海船的通航条件.通过本文的分析，可以看出，在利用本文提出的模型分析后，15万t超大型海船在减载并满足本文提出的通航条件下，是可以安全通过福姜沙水道的.本文的研究成果对超大型海船进江具有指导意义.

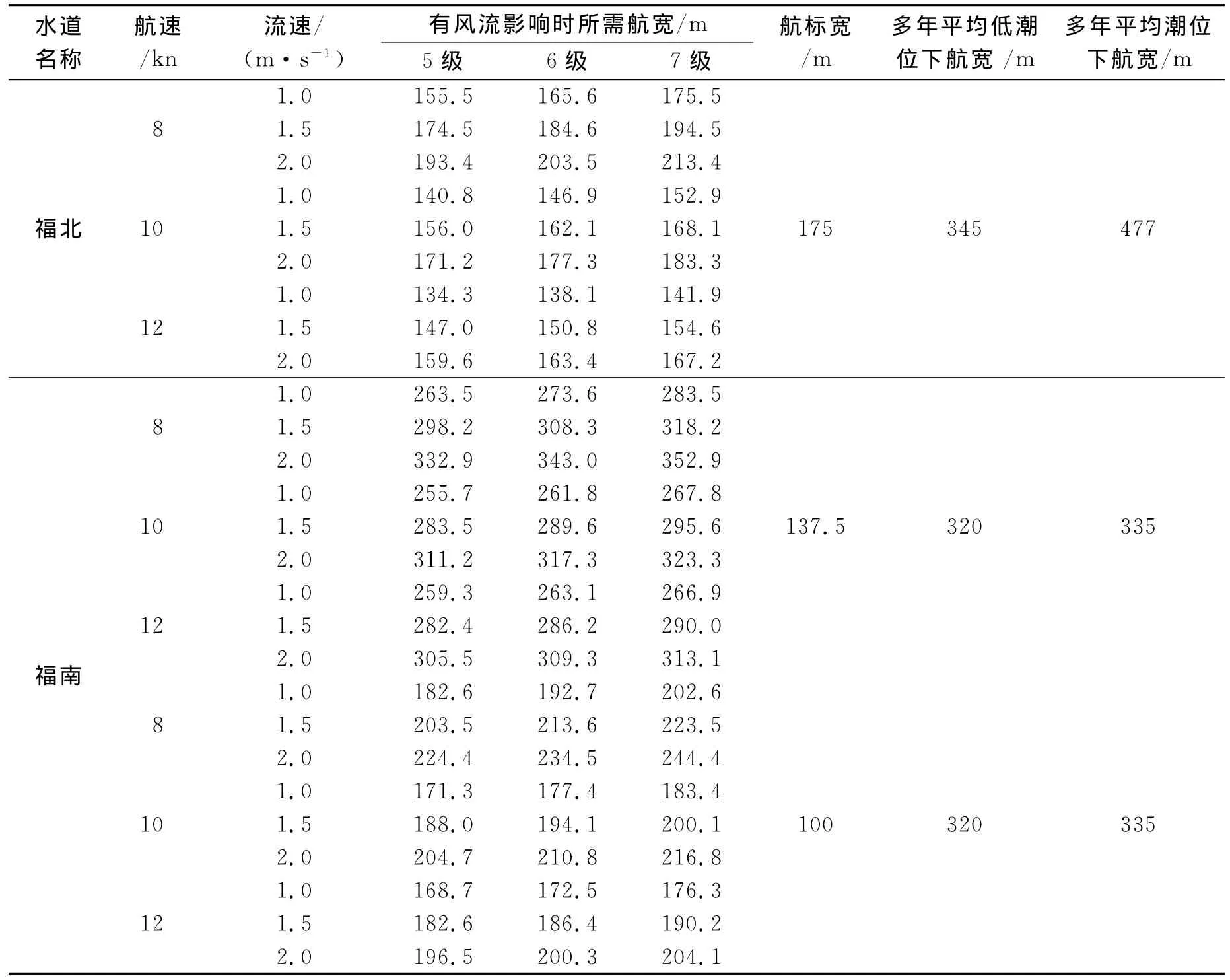
表5 代表船舶通过弯道所需航宽分析表

［1］刘明俊，万长征.航道通过能力影响因素的分析［J］.船海工程，2008（5）：116－118.

［2］刘明俊，周崇喜，杨晓妍，等.苏通大桥船舶通航标准论证方法［J］.船海工程，2005（3）：24－27.

［3］刘明俊，甘浪雄.在风流作用下船舶桥区运动模型探讨［C］／／海船进江与航行安全保障论文集.中国航海学会，2003.

［4］刘明俊，刘先栋，齐传新.船舶（队）通过黄石大桥引航技术研究［J］.航海技术，1999（1）：2－5.

［5］刘明俊，吕习道.船舶过弯道航宽计算及应用［C］／／内河船舶驾驶专业委员会学术年会论文集.中国航海学会，2004.