深度优先搜索算法和A*算法在迷宫搜索中的仿真研究

刘 翔，龚道雄

LIU Xiang,GONG Dao-xiong

（北京工业大学 电子信息与控制工程学院，北京 100124）

0 引言

在现代社会中，火灾、爆炸、坍塌事故常有发生，救援过程中因建筑情况不清，意外坍塌事故等导致救援人员遇难的惨剧时有发生。为避免此类事故，应用机器人及时探知险情和受困人员的情况和位置有着极大的应用意义。论文中将机器人所面临的搜救环境抽象为一个迷宫，而搜救就是要在迷宫中先搜索到目标物并带着目标物返回到出发点处。

迷宫的种类[1]有很多，而用的比较普遍的是Perfect迷宫，所谓的Perfect迷宫是一种没有任何环路且没有任何不能到达的区域。本次实验中，所选择的迷宫环境都为Perfect迷宫。目前，经典的搜索路径算法有D*算法和A*算法，而在迷宫中运用最为普遍的搜索算法是泛洪算法，而泛洪算法是一种基于改进的深度优先搜索算法[2]。泛洪算法在搜索过程中多次遇到目标点，但它的目的是要从这些路径中找到最快到达目标点的一条路径，原始的泛洪算法不适合本次实验中的搜救应用，于是，我们在实验中是用深度优先搜索算法进行比较研究。Takayuki Goto，Takeshi Kosaka研究了A*以及D*算法在ITS（智能运输系统）和机器人路径规划中的应用，确定了A*算法以及D*算法的优势[3]。而对于A*算法中启发式函数的选取，已有多种选择。在启发式函数的选取上，有对A*算法估价函数所出现的问题，将距离和角度进行归一化处理[4]；也有对当前节点进行评估的思想上，增加了最短路径中当前节点的父节点，并对当前节点与终节点的距离进行了评估，这使得A*算法的搜索方向更加趋向终点，从而提高了搜索速度[5]；还有一般情况下对启发式函数的设定选择为两点间的欧几里得距离[6]；

本次实验中，将分别对含有三种不同启发式函数的A*算法与深度优先搜索算法用于迷宫中进行比较仿真研究。

1 实验研究

1.1 实验研究方法

实验研究目的是将算法用于现实搜救中，既然是为了搜救，那么时间是关键，搜索迷宫所用时间的长短就成为评价算法优劣的主要因素。对于机器人来说，所处的迷宫环境是未知的，它只能通过传感器感测到目标点所在的大致位置，然后根据算法一步一步的搜索到目标物。从出发点处找到目标物时所耗的时间我们记录为搜索迷宫所用的时间，当然，搜救的目的不仅仅是为了找到目标物，同时是需要在找到目标物后将目标物带回至出发点处。从目标点返回到出发点时，如果沿之前的原路返回，那就会浪费很多没必要的时间，使搜救时间变长，所以我们要做的工作是要将之前的走过的路径进行优化，使机器人带着目标物返回出发点时不用走“冤枉路”，从而节省搜救时间。

真实环境中，目标物在目标点处通过敲打墙壁或地面等发出声音，模拟“呼救”，从而让机器人通过传感器感知到目标物。但由于外界因素（例如：传感器的精度，迷宫环境中障碍物对声音的阻碍作用等）的干扰会导致机器人只能判断出目标物的大致位置，这个大致位置是随着机器人离目标物越来越近而会越来越精确，直至找到目标物。

而在本次仿真实验中，为了能够比较真实的模拟真实环境，我们人为的让目标点坐标产生了一定的偏差，并且让这个偏差值随着机器人越来越靠近目标点而变得越来越小。

1.2 深度优先搜索算法

所谓“深度优先”，即：状态树的生长或展开，首先沿状态树的深度方向进行。深度优先搜索算法需要记录下状态树的生长过程，深度优先搜索算法是一种盲目的搜索算法，搜索中可能很多次的搜索到目标点，深度搜索算法通过不断剪枝，寻找出一条从起始点到目标点最近且最省时的路径，即深度优先搜索算法也是一种全局的搜索算法，这样的深度优先搜索算法运用到未知迷宫搜救中是没有意义的。而本次实验中，深度优先搜索算法是以找到目标物为目的，没有剪枝的步骤，只要搜索到目标物，迷宫的搜索过程就成功退出。

1.3 A*算法

A*算法是人工智能中的一种搜索算法，是一种启发式搜索算法，它不需遍历所有节点，只是利用包含问题启发式信息的评价函数对节点进行排序（Node Ordering），使搜索方向朝着最有可能找到目标并产生最优解的方向。它的独特之处是检查最短路径中每个可能的节点时引入了全局信息，对当前节点距终点的距离做出估计，并作为评价节点处于最短路线上的可能性的度量。A*算法中引入了评估函数，评估函数如下：

其中：n是搜索中遇到的任意状态。g(n)是从起始状态到n的代价。h(n)是对n到目标状态代价的启发式估计。仿真实验中，我们为A*实现了三种启发式函数，如引言中所述，一种启发式函数为当前点到目标点的欧几里得距离评估，我们定义为A*(1)；

即A*(1)算法的评估函数为：

其中启发式函数h1(i)为当前节点i到偏移目标点的欧几里得距离。

另一种启发式函数在第一种的启发式函数中增加了当前节点的父节点到目标点的欧几里得距离评估，我们定义为A*(2)；

A*(2)算法的评估函数为：

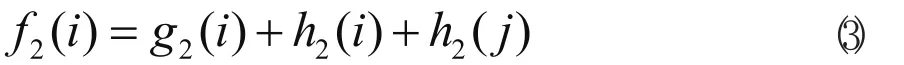
j为当前节点的父节点，h2(i)为已评估出的当前节点i的父节点到偏移目标点的距离。

最后一种启发式函数是在第一种启发式函数的评估上加入了当前点到目标点的角度评估，我们定义为A*(3)。

A*(3)算法的评估函数为：

2 仿真实验分析

实验的迷宫环境设置如下图所示，将环境划分为一个一个的栅格，红色栅格为障碍物，白色栅格为通道，生成的10个迷宫均为Pefect迷宫，保证了整个迷宫中至少有一条从起点到目标点的通道并不会产生环路。起点坐标设为(0,0)，目标点坐标设为(24,24)。

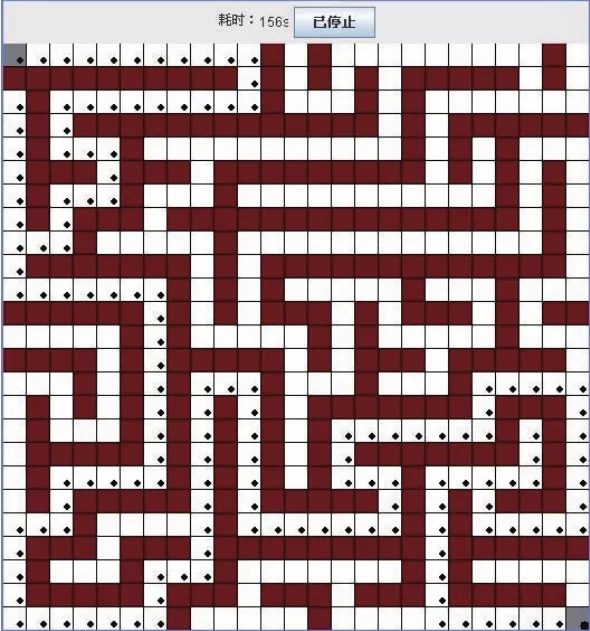
图1 迷宫仿真环境

由于机器人在检测呼救信号时存在不准确因素(例如：传感器的精度，迷宫环境障碍物对声音的阻碍作用等)，都会导致机器人在搜索时存在或多或少的误差，所以仿真实验中，为了比较真实的模拟现实搜救环境，我们对目标点做了偏差处理，处理方式如图2中所示。

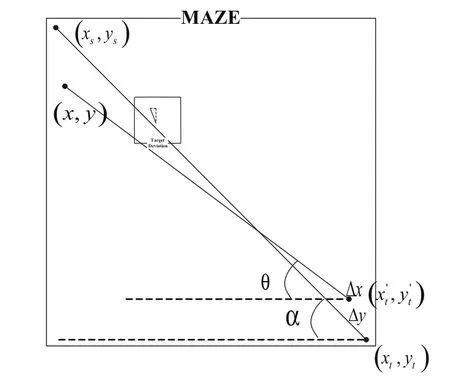
图2 目标点偏差图

其中，(xs,ys)为起始点坐标，(x,y)为机器人当前所在位置坐标，(xt',yt')为偏移目标点的坐标，(xt,yt)为实际目标点坐标：

其中，k为权重值，通过实验，取得k=40，l为当前点坐标到实际目标点坐标的欧几里得距离，L为起始点到实际目标点坐标的欧几里得距离，rand(-1,1)为随机数，随机数的取值范围为(-1,1)。

实验中，我们将三种A*算法分别在10个不同的Perfect迷宫中运行，统计结果如表1所示。

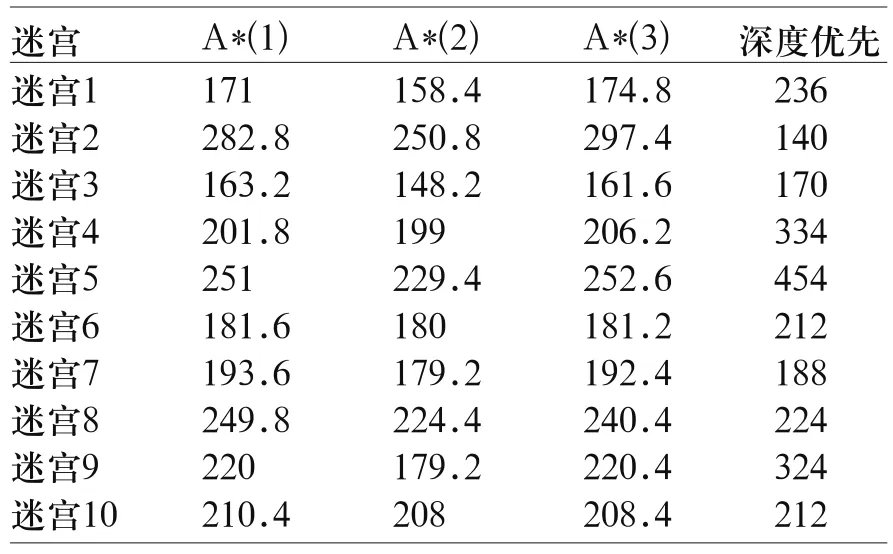
表1 仿真实验比较结果

通过上表的结果分析可知，正如文献3中所述，加入了父节点评估的A*算法（即A*(2)）在搜索时，提高了搜索速度；而在文献2中所述的提高搜索速度的优势在本次实验中没有很好的体现出来，这是因为，在本次实验中，我们加入了偏差值，对于A*(3)中的估价函数，不仅在距离上加入了偏差，同时在角度上也加入了偏差，从而使得A*(3)算法在本次搜索中没有优势。从表中我们还可以得出，带有启发式函数的A*算法要优于深度优先搜索算法。

仿真实验中，对于返回路径的优化，我们通过算法设定，让机器人每走过一个栅格都将该栅格的状态标记为“已访问”，被标记为“已访问”的栅格，机器人在搜索时就不会再走，除非遇到是死路的栅格。那么在算法中我们定义两个状态，一个状态是通过栅格的次数(count)，另一个状态是栅格是否为分支。当机器人搜索到目标点后，返回时只需要走count为1或者栅格为分支(isBranch=true)的路线就是返回的最优路线，且不会走“冤枉路”。

3 结论

本文通过仿真实验比较了A*算法与深度优先搜索算法在未知迷宫中的搜索应用，仿真实验中还同时比较了三种带有不同启发式函数的A*算法的应用，通过仿真实验比较得出的结果是：总体来说，未知迷宫中，在仅知道目标点的大概位置的情况下，进行搜索时，A*算法要优于深度优先搜索算法，而A*算法在启发式函数不同的情况下，搜索产生的结果也是不同的，从上述仿真实验结果的比较中可以得出，A*(2)算法搜索路径的时间是最优的，其次是A*(1)和A*(3)算法。同时，从实物实验比较结果也可以得出，带有启发式函数的A*算法要优于深度优先搜索算法。深度优先搜索算法在未知迷宫中进行搜索时是盲目的，而A*算法在搜索过程中通过引入启发式信息来实现向目标节点移动的判别，无需遍历地图，使得计算复杂度相对较小，实现了快速、高效。但是，这也导致搜索的过程中排除了大量节点，而由于经验及实际问题的复杂性，引入启发信息的代价函数无法做到完全正确，这些被排除的节点可能就是最优路径的节点之一。

[1] http：//www.astrolog.org/labyrnth.htm.

[2] A.Francy Golda,S.Aridha,and D.Elakkiya,"Algorithmic Agent for Effective Mobile Robot Navigation in an Unknown Environment."Intelligent Agent & Multi-Agent Systems,2009,IAMA 2009.

[3] Takayuki Goto,Takeshi Kosaka,and Hiroshi Noborio,"On the Heuristics of A* or A Algorithm in ITS and Robot Path-Planning,"Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems,pp.1159-1166,Oct,2003.

[4] 史辉,曹闻,朱述龙,"A*算法的改进及其在路径规划中的应用"[J].测绘与空间地理信息,2009,32,6：208-211.

[5] 张仁平,周庆忠,熊伟,"A*算法改进算法及其应用"[J].计算机系统应用,2009,98-100.

[6] Hiroshi Noborio,Keiichi Fhjimura,Yohei Horiuchi,"A Comparative Study of Sensor-Based Path-Planning Algorithms in an Unknown Maze,"Proceedings of the 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems,2000,909-916.