磁悬浮电主轴单元径向轴承的磁场分析
廖 萍 ,马苏扬 ,吴国庆,茅靖峰,姜安栋,夏正鹏
LIAO Ping,MA Su-yang,WU Guo-qing,MAO Jing-feng,JIANG An-dong,XIA Zheng-peng
(南通大学 机械工程学院,南通 226019)
0 引言
数控机床正在朝着高速度、高精度、高效、高智能化的方向发展[1],制造业对加工设备的性能提出了越来越高的要求,这种需求促进了机床工业,尤其是数控机床的发展。但与数控机床配套的功能部件的产业化规模和产品水平,远远满足不了数控机床的发展要求[2]。主轴组件是机床中最重要的部件之一,其性能优劣,尤其是其径向旋转精度(指装配后,在无载荷、低速转动条件下,主轴前端安装工件或刀具部位的径向跳动[3])和运动精度(指主轴以工作速度转动时的旋转精度),将直接影响到被加工零件的形状和尺寸精度[4]。
电主轴单元将高速电机与精密主轴有机结合,取消了传统机床从动源(电机)到主轴之间的传动带、齿轮等诸多机械传动环节,实现了机床主传动系统的“零传动”,具有损耗低、寿命长、精度高、转速高、振动低等优点[5]。目前,电主轴单元已成为高速数控机床的核心功能部件之一。
电主轴单元中的支承轴承大多采用混合陶瓷球轴承等机械接触式轴承[6],这类轴承虽然具有温升小、刚度大、寿命长、极限转速高等优点,但应用在长时间高速加工场合时仍存在缺点,一方面由于接触疲劳产生轴承失效,需定期更换轴承,另一方面,由于高速摩擦产生的热量通过轴承内圈传递到主轴,引起主轴的不均匀热变形。磁悬浮支承技术利用磁场力将物体悬浮,实现了无接触式支承[7]。将磁悬浮支承技术与电主轴单元相结合制成磁悬浮电主轴单元,具有定位精度高、无需润滑、无接触摩擦、低功耗、刚度大、机床噪音低、切削精度高等优点[8,9],是未来数控机床主轴单元的发展趋势。
1 磁悬浮电主轴单元工作原理及磁力计算
磁悬浮电主轴单元剖面结构如图1所示。
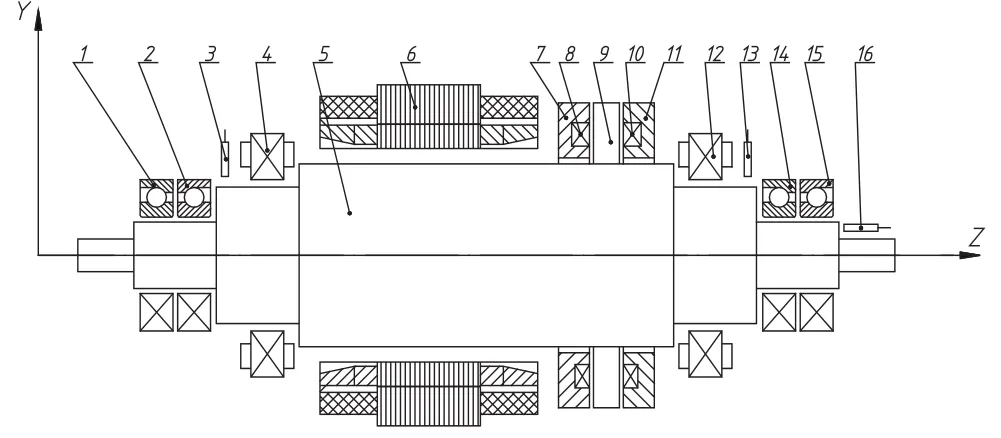
图1 磁悬浮电主轴单元剖面结构图
其工作原理为:主轴单元未工作时,主轴由辅助支承轴承1、2、14、15支承,当主轴单元工作时,径向磁轴承4、12以及轴向磁轴承7、11中线圈通电,对主轴5产生Y方向与Z方向的电磁力,使得主轴稳定悬浮。由于承受主轴自重和外加载荷的作用,上下磁极磁吸力大小不一致,上磁极磁吸力为F1,下磁极磁吸力大小为F2,F1〉F2,其磁吸力大小分别为[10]:
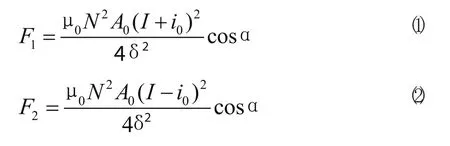
式中,µ0—真空磁导率;N—线圈匝数;I—偏置电流;i0—主轴克服自重的控制电流;A0—单个磁极面积;δ—单边气隙值;2α—两磁极夹角。
由(1)、(2)式可得主轴在自重下悬浮的吸力方程为:
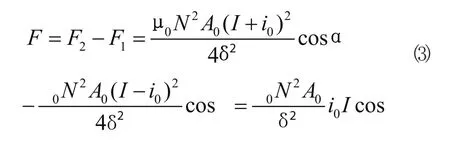
主轴稳定悬浮后,由电机6带动主轴旋转,径向位移传感器3、13与轴向位移传感器16分别用于检测主轴稳定悬浮时在Y方向与Z方向上的位置。
当主轴在Y方向上或Z方向上受到外界扰动时,由径向位移传感器或轴向位移传感器检测出主轴偏移方向以及偏移量,并将检测信号反馈给控制器,控制器根据反馈信号调整线圈中的电流大小,使得主轴回到平衡位置。设计时上下磁极与左右磁极各采用一个控制器,采用差动控制原理。以上下磁极为例,其工作原理如图2所示,设某一时刻出现一垂直向上扰动,使主轴向上偏移平衡位置x,为使主轴回到原来的平衡位置,必须加一控制电流ic即:
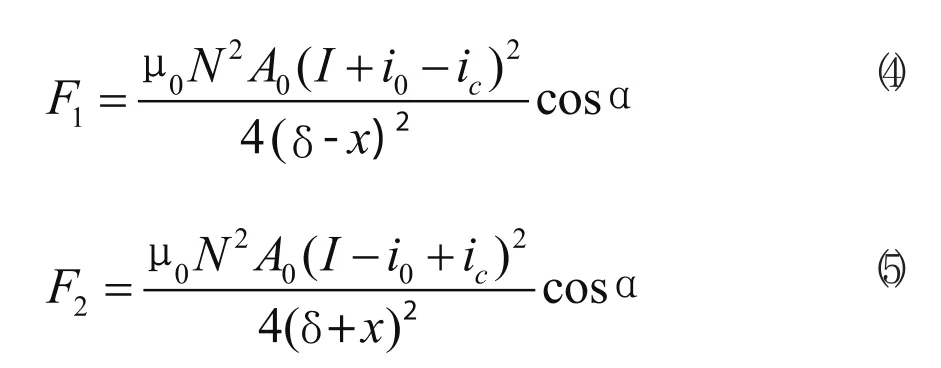
此时主轴所受合力为:
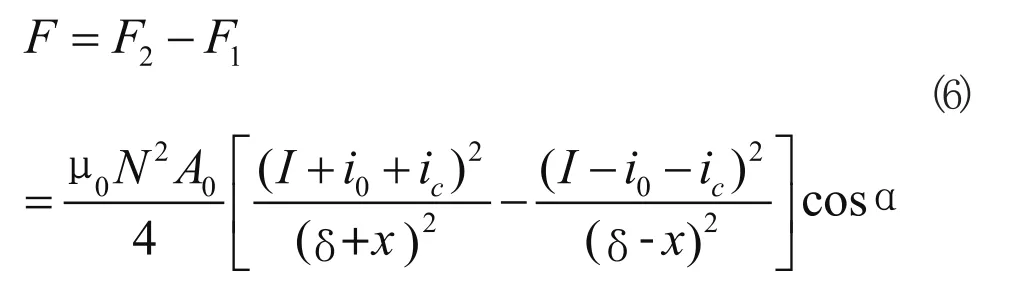
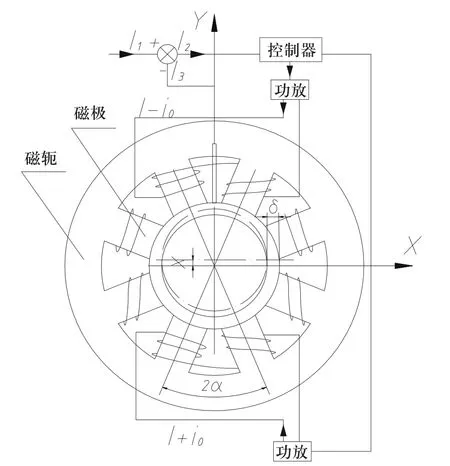
图2 径向磁轴承差动控制结构
由此可见,在控制电流ic的调整下,上磁极磁力减小,下磁极磁力增大,主轴又回到平衡位置进行工作。
2 单边气隙值对磁悬浮电主轴单元径向轴承电磁场的影响
2.1 单边气隙值的选择
由公式(3)可知,单边气隙值δ的大小对磁力轴承的性能有较大影响,一般δ=0.2~0.5mm,取较大值时可降低主轴单元加工装配的难度,但若δ值过大,又将导致磁场磁漏增加,控制系统的稳定性难以保证,因此,需对单边气隙值进行优化。根据设计的磁悬浮电主轴单元特征,采用ANSYS软件首先进行二维静态磁场的分析,磁轴承参数选择如下:I=1A,i0=0.478A(实际工作时,控制电流i0会随切削力的变化而进行调整,使得主轴始终处于稳定悬浮的位置),A0=441mm2,N=192,2α=45°,主轴径向支承轴颈公称尺寸60mm,主轴在自重下悬浮时Z方向单个径向磁轴承承载力为100N,得到单个主轴在径向磁轴承中稳定悬浮时单边气隙值为0.2~0.5mm时的磁力线分布如图3所示。
从磁力线分布图可以看出,在线圈匝数、电流、磁极面积一定时,磁路磁漏随单边气隙值的增大而增大。单边气隙值为0.2mm时,磁路磁漏很少,径向磁轴承内磁力线分布较集中;当单边气隙值为0.5mm时,磁路出现较多磁漏;当单边气隙值取0.3mm或0.4mm时,磁场磁漏相差不大,但单边气隙值取值较大时,在同样的承载力下,磁悬浮电主轴单元的结构尺寸会增大,因此,本例中单边气隙值选取0.3±0.04mm。
2.2 单边气隙不均匀性对径向磁轴承磁场的影响
上述分析均是基于单边气隙均匀情况下进行的,但径向磁轴承磁极内圈和主轴支承轴颈不可避免的存在圆度误差,引起单边气隙的不均匀。如图4(a)或4(b)所示,设磁轴承磁极内圈或主轴支承轴颈处的圆度误差为零,主轴支承轴颈处的圆度误差为δ1或磁轴承磁极内圈圆度误差为δ2,则磁极内圈或支承轴颈可看作一个假想的圆,当主轴旋转时,δ1或δ2将引发单边气隙值的不均匀,这种不均匀性打破了主轴径向力的平衡,致使其瞬间回转中心线(实际中心线)相对于理想中心线发生偏离,引起回转主轴在该瞬间的径向误差,即所谓的主轴径向旋转精度。因此,分析主轴支承轴颈圆度误差与径向磁轴承磁极内圈圆度误差,对研究磁悬浮电主轴单元的工作性能具有重要意义。
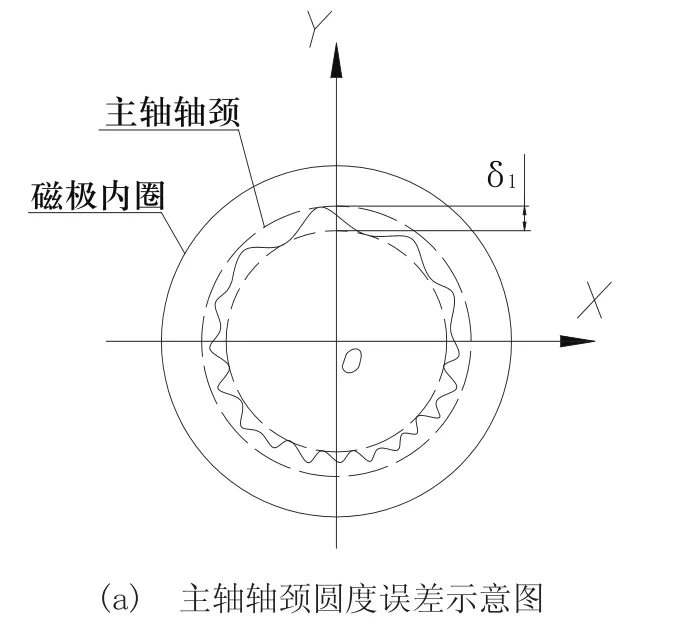
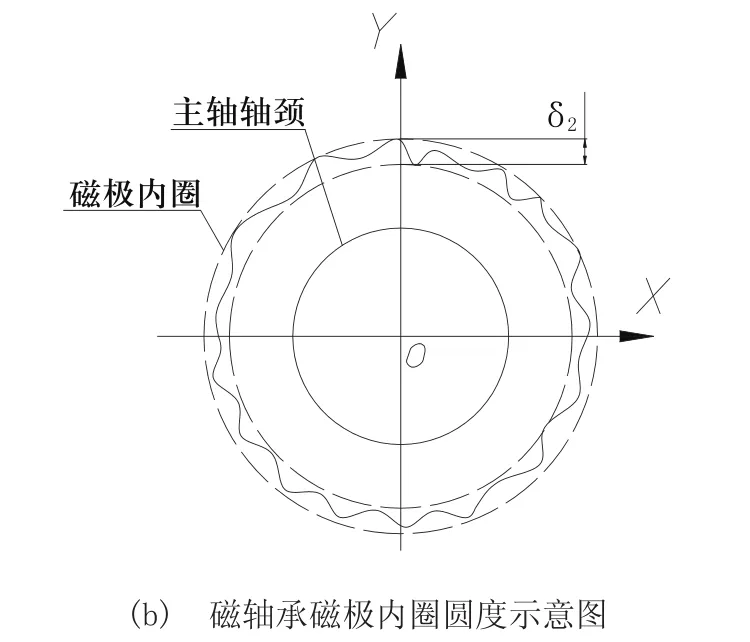
图4 磁轴承圆度误差示意图
根据一般5.5kW电主轴单元主轴设计原则,取主轴轴颈圆度误差为0.003mm,分析磁极内圈不同圆度误差引起的气隙不均匀对径向磁轴承磁场的影响。当单边气隙值取0.3mm时,圆度误差一般不超过0.2mm,由图3可得,此时的磁场磁漏对径向磁轴承的影响较小,因此,应主要考虑两者圆度误差对径向磁轴承电磁力的影响。
图5列出了同时考虑径向磁轴承磁极内圈圆度误差和主轴支承轴颈圆度误差时,气隙变化的4个极限位置。当主轴位于这四个位置时,其所受实际电磁力大小与理论值误差具有极值。图中原点o为主轴的理想中心线位置,1、2分别为径向轴承磁极内圈以及主轴轴颈的圆度误差均为0时的理想廓线,3、4分别为主轴支承轴颈和径向磁轴承磁极内圈廓线,为便于分析,3、4均仅画出圆度误差最大峰值点δ1、δ2。
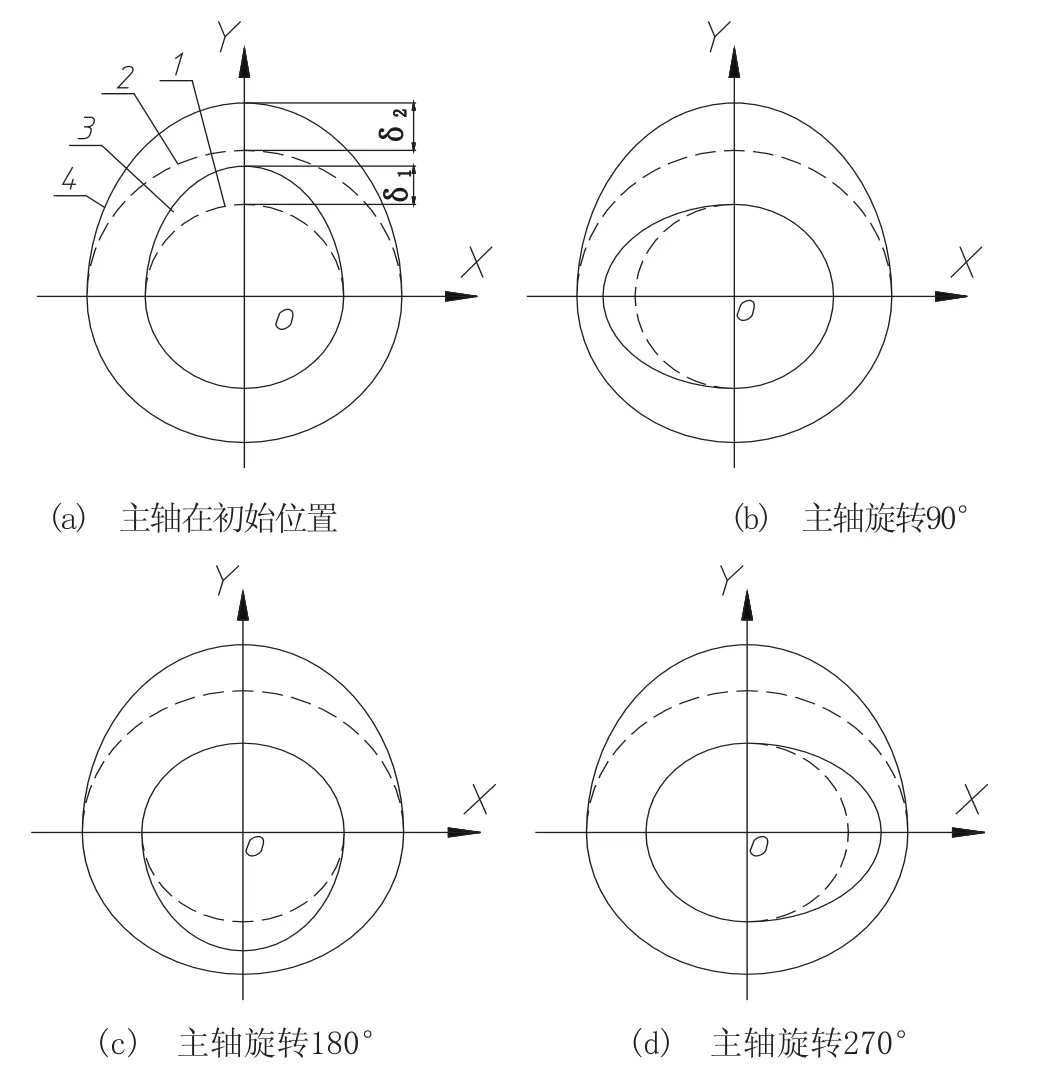
图5 主轴旋转极限位置示意图
图6为径向磁轴承磁极内圈圆度为0.001~0.012mm,主轴与径向磁轴承位置关系分别如图5(a)~图5(d)所示时,主轴所受实际电磁力大小变化曲线图。其中,横坐标为径向磁轴承内圈圆度误差值,纵坐标为主轴所受电磁力大小,a、c、d分别为主轴在图5(a)、5(b)、5(c)所示位置时所受电磁力大小随径向磁轴承磁极内圈圆度变化曲线;b为主轴与径向磁轴承内圈圆度均为0时主轴所受电磁力大小。由图6可知,主轴位于不同位置时,其所受电磁力大小随径向磁轴承内圈圆度的增加均呈减小趋势。当主轴位于图5(a)位置时,随着径向磁轴承内圈圆度的增加,主轴所受实际电磁力大小先靠近再偏离理论值,这主要是由于主轴轴颈圆度的存在,使得主轴上端处与径向磁轴承磁极内圈之间的单边气隙值小于0.3mm,径向磁轴承上磁极产生电磁力增大;主轴下端与径向磁轴承磁极内圈单边气隙值未发生变化,径向磁轴承下磁极电磁力不变,主轴在竖直方向所受电磁力合力增大。随着径向磁轴承磁极内圈圆度的增加,主轴上端处单边气隙值慢慢接近0.3mm,主轴在竖直方向上所受电磁力合力减小,与理论值误差也减小。当径向磁轴承磁极内圈圆度达到0.003mm时,主轴上端单边气隙值最接近0.3mm,此时主轴竖直方向上所受电磁力合力最接近理论值。当径向磁轴承磁极内圈圆度继续增大时,主轴上端处单边气隙值大于0.3mm,径向磁轴承上磁极产生电磁力减小,主轴所受电磁力合力减小,此时,主轴所受实际电磁力合力大小与理论值误差随径向磁轴承磁极内圈圆度的增加而增大。
当主轴旋转到图5(b)位置时,主轴上端处的单边气隙值随着径向磁轴承磁极内圈圆度的增加而增大,而主轴下端处单边气隙值变化很小,使得径向磁轴承上磁极产生电磁力减小,下磁极产生的电磁力变化量很小,主轴在竖直方向上受到的电磁合力减小。径向磁轴承磁极内圈圆度越大,主轴竖直方向上电磁合力减小的越大,与理论值误差越大。
当主轴旋转到图5(c)位置时,由于主轴下端处与径向磁轴承磁极内圈之间的单边气隙值小于0.3mm,径向磁轴承下磁极产生电磁力增大;主轴上端与径向磁轴承磁极内圈单边气隙值仍为0.3mm,径向磁轴承上磁极电磁力不变,主轴在竖直方向所受电磁力合力减小。随着径向磁轴承磁极内圈圆度的增大,主轴上端处的单边气隙值增大,上磁极产生电磁力逐渐减小,主轴实际所受电磁力合力大小与理论值误差越来越大。当主轴旋转到图5(d)时,其情况与图5(b)一致,主轴所受电磁力大小随径向磁轴承内圈圆度变化曲线与曲线b一致。
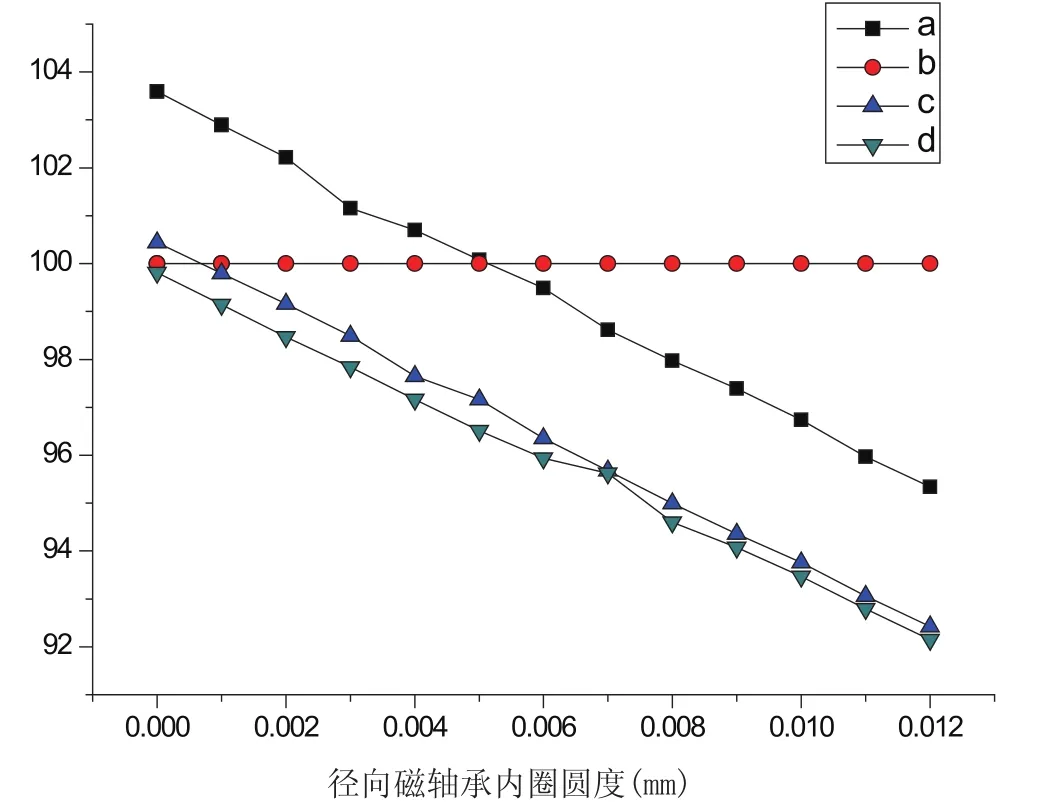
图6 主轴旋转到特殊位置时磁轴承内径圆度为不同值时电磁力大小
由上述分析可得,当主轴径向磁轴承支承处轴颈圆度取0.003mm,径向磁轴承磁极内圈圆度取0.007mm时,主轴旋转一周时在任何位置时所受实际电磁力大小与理论值误差不超过5%,此时主轴所受合力5N,由传感器检测出主轴偏离平衡位置到控制器发出信号调整控制电流所需时间大约为8毫秒~10毫秒之间,通过计算可知,主轴径向偏移理想中心线的最大偏移量为0.0025mm,满足精密加工要求。因此,本例中,主轴支承轴颈圆度为0.0025mm时,径向磁轴承磁极内圈圆度取0.007mm。
3 结论
通过对磁悬浮电主轴单元径向轴承的电磁场分析,可得出如下结论:
1)采用ANSYS有限元分析程序对实例进行了仿真计算与分析,得出了不同单边气隙值下径向磁轴承的磁场磁漏情况。对于功率为5.5KW的电主轴,当单边气隙值取为0.3±0.04mm时,其磁场磁漏小、结构紧凑。
2)当主轴径向磁轴承支承处轴颈圆度为0.003mm,径向磁轴承磁极内圈圆度为0.007mm时,主轴径向偏离理想中心线的最大偏移量为0.0025mm,主轴具有较高的径向旋转精度,可满足精密机床工作要求。
[1] Liping Fan and Yi Liu,Iterative Learning Control for Linear Motor Motion System,Proceedings of the IEEE International Conference on Automation and Logistics,18-21 Aug.2007 Jinan,China,pp:2379-2383.
[2] 马苏扬,吴国庆,吴爱华,朱昱,廖萍.直接驱动型磁悬浮直线进给单元[J].机床与液压,2010,38(7):22-25.
[3] 戴曙.金属切削机床设计[M].北京:机械工业出版社,1982.
[4] 李玉亭,李丽,李彦,陈长江.数控机床用电主轴[J].机械研究与应用,2009,(3):125-128.
[5] Jastrzebski RP,Hynynen KM,Smirnov A.H-infinity control of active magnetic suspension[J].Mechanical Systems And Signal Processing,2010,24(4):995-1006.
[6] 汪建平,巫少龙.基于MATLAB数控机床电主轴陶瓷球轴承的优化[J].组合机床与自动化加工技术,2008,(8):86-90.
[7] Lee DH,Park JB,Joo YH,et al.Robust H-infinity Control for Uncertain Nonlinear Active Magnetic Bearing Systems via Takagi-Sugeno Fuzzy Models[J].International Journal Of Control Automation And Systems,2010,8(3):636-646.
[8] Kang MS,Lyou J,Lee JK.Sliding mode control for an active magnetic bearing system subject to base motion[J].Mechatronics,2010,20(1):171-178.
[9] 朱益民,龚建伟,沙小红.磁悬浮实验系统的设计与分析[J].南通大学学报(自然科学版),2005,4(4):16-18.
[10]吴华春.磁力轴承支承的转子动态特性研究[D].武汉:武汉理工大学,2005.

