静态小波相关滤波法在振动信号处理中的应用
张 丹, 隋文涛,李志永,季 画
ZHANG Dan1,SUI Wen-tao2,LI Zhi-yong2,JI Hua1
(1. 山东理工大学 电气与电子工程学院,淄博 255049;2. 山东理工大学 机械工程学院,淄博 255049)
0 引言
许多机械是在非平稳状态下工作,采集的振动信号往往受到噪声信号干扰。研究机械振动信号的滤波消噪,对机械设备的故障诊断有着重要的理论和实践意义[1,2]。
传统的消噪方法是根据信号和噪声的频谱分布规律,采用滤波器进行信号降噪。先采用傅里叶变换降含噪信号变换到频域,然后采用低通滤波器进行去噪。但是,当噪声和信号的频带有重叠时,比如信号含有白噪声,低通滤波去噪效果较差。传统的消噪方法的理论基础是傅里叶变换,存在保护信号局部特性和抑制噪声之间的矛盾。小波变换具有良好的时频局部化特性,在信号消噪中得到广泛的研究并取得了非常好的应用效果,成为信号去噪的主要方法之一。
为了有效提取振动信号中的故障特征,本文提出将静态小波变换和尺度相关滤波相结合的方法。先对信号进行静态小波分解,再利用尺度相关法分离信号与噪声,提出了一种针对振动信号的噪声能量阈值估计算法。实验结果表明,静态小波尺度相关滤波法较好的保留了振动信号的边缘特征,为故障特征提取创造了良好的条件。
1 静态小波变换
为了方便计算机进行分析、处理,信号都要离散化为离散序列,得到离散小波变换,记为DWT(Diserete Wavelet Transform)。
Mallat算法是计算离散小波变换的快速算法。在Mallat算法中,输入信号分别经过低通和高通滤波器卷积后,进行隔二取一的下采样得到尺度系数和小波系数。但由于DWT中进行了下采样,得到的小波系数缺乏平移不变性。
静态小波变换(stationary wavelet transform,SWT)的引入在一定度上解决了该问题。
静态小波变换(SWT)与离散小波变换相同之处在于在每层上都运用高通和低通滤波器对输入信号进行处理,不同之处是静态小波变换不对输出信号进行下采样,而是进行上采样。
假设s[n] 的长度为N,其中N= 2J,J为整数。h1[n] 和 g1[n] 是由正交小波确定的高通滤波器和低通滤波器。在第一层,输入信号x[n]与h1[n] 相卷积得到近似小波系数a1[n],与g1[n]相卷积得到细节小波系数d1[n]。

因为没有进行下采样,所以a1[n]和d1[n]的长度都是N ,而不同于离散小波变换中的长度N/2。在静态小波变换的下一个分解层次a1[n]分解成如同前述的两部分,h2[n]] 和g2[n] 分别为h1[n]和g1[n]]通过上采样得到。分解过程如图1递归进行。



图1 静态小波分解图
2 尺度相关滤波
2.1 尺度相关降噪原理
Witkin[3]首先提出了使用尺度空间相关性来对信号滤波的思想,对含噪信号经过多尺度小波分解后,从粗尺度到细尺度逐步搜索信号的主要边缘,最终从噪声信号中得到真实信号,Xu[4]在此基础上提出了尺度相关滤波方法。具体阐述为:信号的突变点在不同尺度的同一位置都有较大的峰值出现,噪声能量随着尺度的增大而减小。因此,可以取相邻尺度的小波系数直接相乘进行相关计算。由于信号的突变点有良好的局部性质,并且出现在各尺度上,而噪声的能量却集中在小尺度上,其小波系数随着尺度的增大而迅速衰减。因此,可以利用小波系数在不同尺度上对应点处的相关性来判断是信号系数还是噪声系数,从而达到降噪的目的。
2.2 尺度相关降噪算法
尺度相关降噪算法如下:
1)计算每个尺度j的相关性函数Corr2(j,k)。
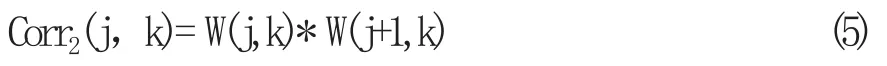
其中,W(j,k)是j尺度位置k处的小波系数。
2)对Corr2(j,k)重新归一化,使其归一化到W(j,k)的能量上去,得到
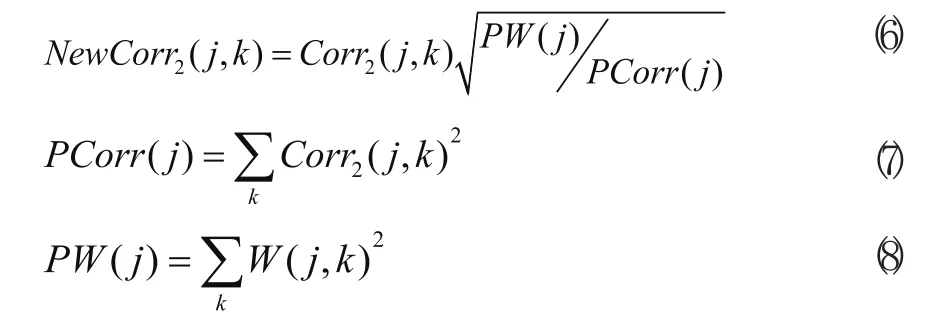
3)如果|NewCorr2(j,k)|≥|W(j,k)|,则认为该点为信号的重要部分,将W(j,k)赋予Wnew(j,k),并将Corr2(j,k)和W(j,k)置0。否则,认为该点由噪声引发,保留Corr2(j,k)和W(j,k)。
4)重复步骤2)、3),直到W(j,k)满足某个尺度j上的噪声能量阈值为止。
把从W(j,k)中抽取的数据点组成一个新向量,记作Wnew(j,k)。显然Wnew(j,k)中保留了大部分的边缘,且去除了大部分的噪声。最后,根据滤波后的数据Wnew(j,k)重构回去,就可得到滤波后的信号。
由于相关滤波中涉及噪声能量阈值的设定,且噪声能量阈值的设定没有通用的算法,因此非常必要给出一种针对振动信号的噪声能量阈值设定算法[5]。
由于振动信号平稳段对应为信号的噪声,若对该含有噪声的振动信号进行多尺度小波分解。取小波变换高频系数的一部分,本实验中取序号100-200,用这些点的方差来估计振动信号的噪声能量阈值。
2.3 仿真验证
用外圈故障仿真信号对降噪算法进行对比。图2 中(a)和(b)分别是仿真信号和加噪后信号。经过不同方法降噪后,如图3所示。静态小波相关算法最有效,小波变换阈值去噪处理后的信号,虽然光滑,但是丢失了很多信息。单独采用平稳小波得到的信号最平滑,但是冲击信息丢失也最严重。

图2 仿真信号和加噪后信号

图3 本文算法与其它降噪算法效果对比
3 实验验证
3.1 实验数据
实验滚动轴承为SKF公司的深沟球轴承,型号为6205-RS。轴承的尺寸信息和故障特征频率信息如表1所示。其中,BSF、BPFI 、BPFO分别代表滚动体故障频率、内圈故障频率、外圈故障频率。

表1 轴承规格与故障特征频率
3.2 实例分析
运用本文提出算法进行滚动轴承振动信号分析,步骤如下:
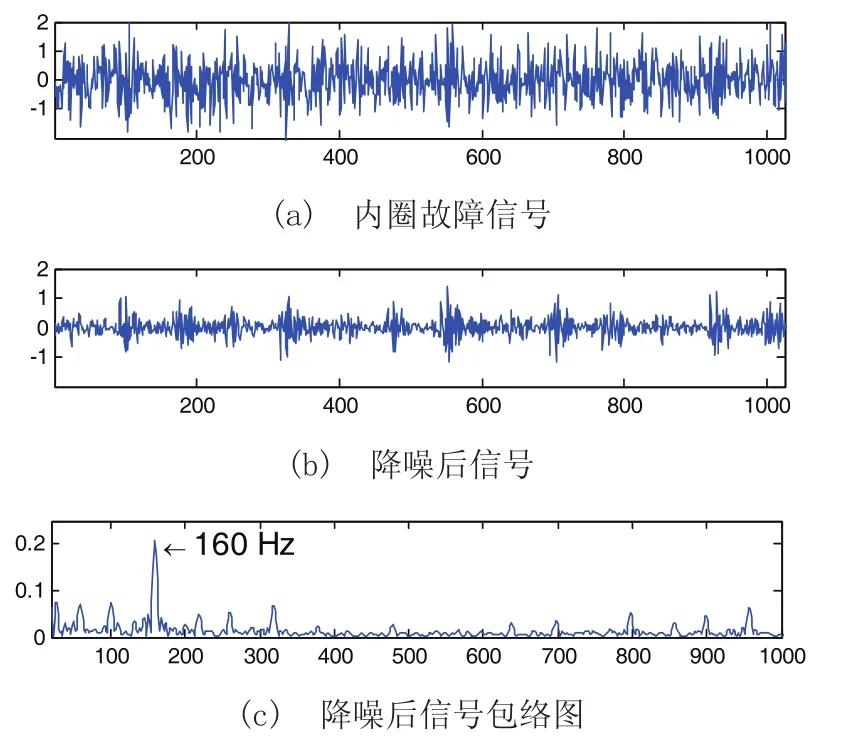
图4 本文方法分析内圈故障信号
从图4可以看出,故障信号非常微弱,已经基本上被噪声所淹没,时域图无法区分故障的存在和故障模式,采用直接进行包络分析,诊断效果不是很好。但是采用本文算法,对内圈故障信号经过降噪后,再进行包络分析,可以非常清楚的判别故障。在图4(c)中清楚显示160Hz处存在峰值,正好对应内圈故障特征频率,也就意味着内圈存在缺陷。
4 结论
本文首次将基于静态小波变换的尺度相关降噪方法用于振动信号处理。经过实例验证,取得了比较好的滤波效果,为后续信号处理提取故障特征提供保证。
[1] 程发斌.面向机械故障特征提取的混合时频分析方法研究[D].重庆:重庆大学,2007.
[2] 郑海波.非平稳非高斯信号特征提取与故障诊断技术研究[D].合肥:合肥工业大学,2002.
[3] Witkin A.Scale space filtering[A].Processing of 8th International Joint Conference Artificial Intelligence[C].Karlsruhe,Germany:IEEE,1983:1019-1021
[4] Xu Y S,John B W,Denis M H,eta1.Wavelet transform domain filters:a spatially selective noise filtration technique[J].Trans on Image Processing,1994,3(6):747-758.
[5] 李仲宁,罗志增.基于小波变换的空域相关法在肌电信号中的应用[J].电子学报,2008,35(7):1414-1418.

