基于流固耦合的U型管流致振动数值分析

庞天照 郭 伟 盛元平 郭 涛

1海军驻葫芦岛431厂军事代表室，辽宁 葫芦岛125004 2海军驻沈阳地区军事代表局，辽宁 沈阳110003 3华中科技大学 船舶与海洋工程学院，湖北 武汉 430074

基于流固耦合的U型管流致振动数值分析

庞天照1郭 伟1盛元平2郭 涛3

1海军驻葫芦岛431厂军事代表室，辽宁 葫芦岛125004 2海军驻沈阳地区军事代表局，辽宁 沈阳110003 3华中科技大学 船舶与海洋工程学院，湖北 武汉 430074

利用ANSYS＋CFX双向耦合的方法对换热器U型管的流致振动问题进行仿真分析。分别建立大涡模拟的流体控制方程和结构振动的控制方程，得到掠过U型管流体的升力系数、阻力系数曲线以及U型管振动加速度级谱线。分析表明，结构振动的主要频率成分在流体升力和阻力变化频率和结构本身的固有频率附近，可为工程实践提供参考，具有理论和实践价值。

流致振动；流固耦合；大涡模拟

1引言

壳管式换热器是石油化工、机械动力、船舶海洋等领域应用十分广泛的热交换设备，换热器的性能对产品质量和可靠性起决定性的作用。壳管式换热器的内部流体流动十分复杂，管束的振动是不可避免的，这是造成换热器疲劳破坏的主要原因。据报道，国内外很多换热器受损都是由于管束的振动引起的［1－3］。因此，研究换热器管束的振动情况对于换热器设计和改进有重要的指导作用，对于安全生产更是亟不可待。

目前，国内外学者对换热器振动机理进行了广泛的研究。到目前为止，国内外比较认同的流体诱导结构振动的机理主要有：漩涡脱落、紊流抖振、流体弹性不稳定以及声振荡［4］。本文将针对换热器内的单根U型管进行流通耦合分析，为换热器的整体分析提供分析方法与参考。

2 相关控制方程

2.1 流体控制方程和大涡模拟

对于不可压缩的粘性流体，在直角坐标系下，其连续性方程可以表示为：

运动形式可以用Navier－Stokes方程来表示：

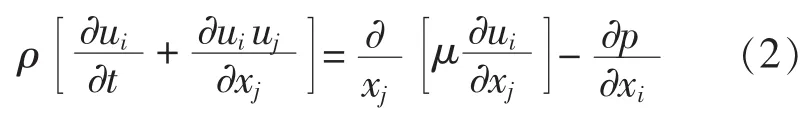
式中，u为流体速度；ρ为流体密度；μ为动力粘性系数；p为静压。

本文采用流体控制方程和大涡模拟（LES）方法来计算流体区域。LES方法将流场的流动变量分为可解的大尺度的涡和不可解的小尺度的涡，然后通过瞬态的Navier－Stokes方程求解大尺度的涡，而将小尺度的涡忽略。

任何流场的流动变量都可以写成如下形式：

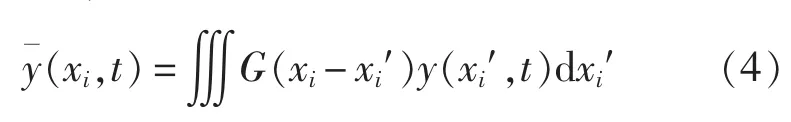
式中，G（xi－xi′）为高斯滤波器。

连续性方程（1）和Navier－Stokes方程（2）经滤波后可以表示为：

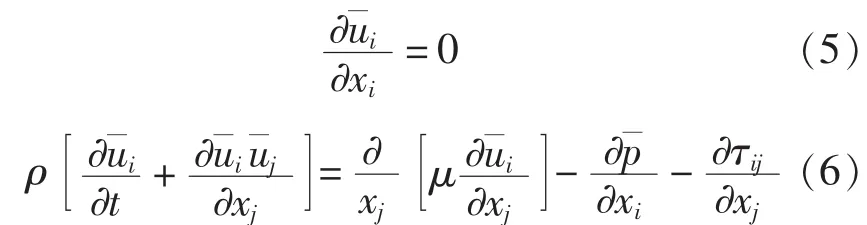
2.2 管束控制方程

首先对换热器的管束振动模型进行合理的简化。管束振动过程中，管束各个位置的横截面并没有发生变形，而只是管束横向的振动。所以管束的控制方程可以表示为：

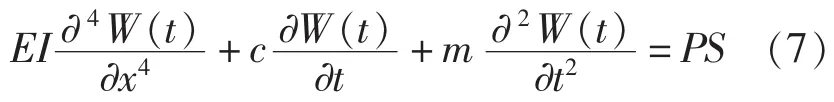
式中，E为杨氏模量；I为惯性矩；c为阻尼；m为包含附连水质量之后的质量；W（t）为绕度；P为管束受到流体的压强；S为面积。

在CFD计算中可以得到管束上各个节点的压强。将CFD计算中得到的压强施加到管束上可以计算出管束的W（t），即实现单向流固耦合。若将每一步得到的W（t）带回流体计算中，进行反复迭代，即可以实现双向的流固耦合过程。

3 数值计算模型和设置

本文利用ANSYS＋CFX软件对换热器壳程内流体诱导的管束振动问题进行相应的分析。

换热器U型管的尺寸为：直径D＝10 mm，厚度t＝1 mm，长度L＝500 mm，R＝20 mm，L0＝20 mm；流体区域的尺寸为：L1＝12×D，L2＝24×D，H＝600 mm，如图1所示。图中左端为进口，边界条件设置为进口速度，u＝1 m／s；右端为出口，边界条件设置为自由出口。U型管壁面设置为非滑移壁面（no slip wall）；其他壁面同样设置为no slip wall，其原因是本文模拟的是有界区域流动。

U型管管外流体区域为60°的空气，U型管管内流体为20°水，U型管材质为钛合金，相关参数如表1所示。

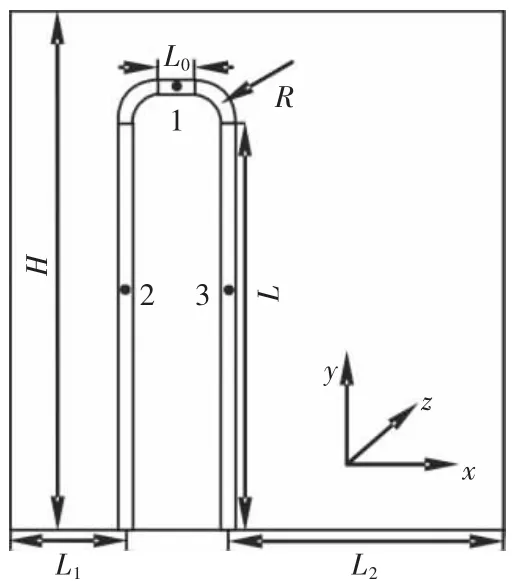
图1 U型管结构示意图Fig.1 Structure diagram of U-tube

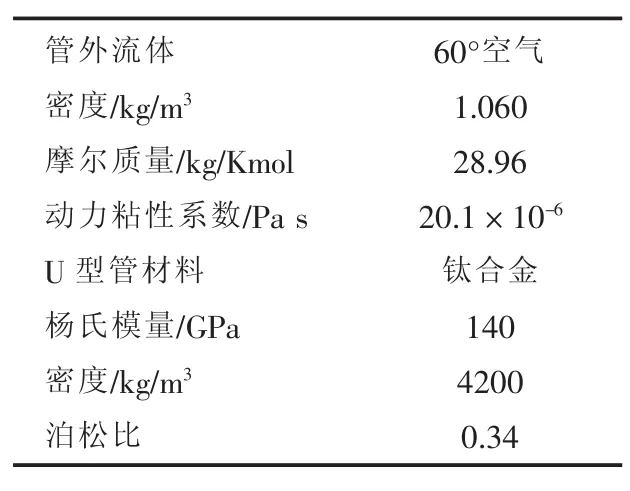
表1 材料参数Tab.1 Material parameters

换热过程中，管内管外的流体运动均会引起换热管束的振动响应，本文主要研究管外流体运动时对换热管束的响应，忽略了管内流体运动对其响应的影响。由于管内流体密度大，对管束系统固有频率的影响较大，不可忽略，故将管内流体等效为管束附连水质量加以考虑，管外流体质量忽略不计。附连水质量效应通过U型管的当量密度来反映，当量密度的计算公式如下：

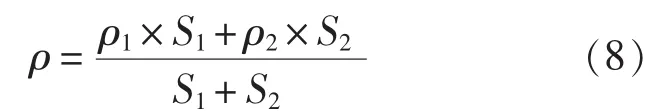
式中，ρ1为U型管的密度；ρ2为管内水的密度；S1为U型管的横截面面积；S2为管内水的横截面面积。

在ICEM CFD中划分流体区域的计算网格，在ANSYS中划分结构的网格，二者之间的耦合面上的节点不需要保持协调，计算中通过插值过程实现二者的数据传输。流体区域的网格如图2所示，流体区域节点数为557 020，单元数为534 280，计算中采用的中心查分格式，收敛残差设置为10－4。文中计算载荷步设置为0.001 s，总的计算时间为1.5 s。

图2 流体区域网格Fig.2 Fluid region grid

4 相关变量定义

4.1 升力系数和阻力系数

将沿U型管长度方向（y方向）的平均升力系数和阻力系数定义为：

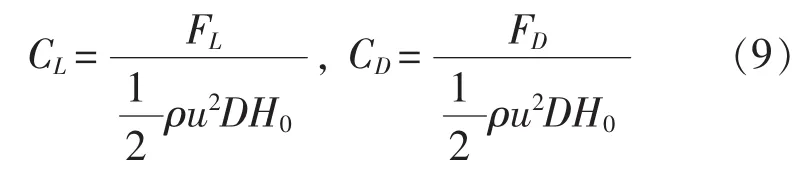
式中，FL为U型管受到来流的升力 （与来流方向垂直）；FD为U型管受到来流的阻力（与来流方向相反）；u为来流速度，H0＝2（L＋R）。

4.2 振动加速度级

振动加速度级是反映结构振动的重要指标，通过对振动加速度级的分析比较，可以评估结构的振动强弱。振动加速极的定义如下：

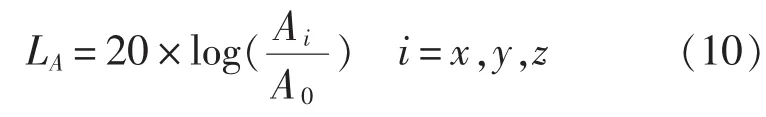
式中，Ai为结构振动i方向的加速度；A0为基准加速度，其值1.0×106。

5 计算结果

5.1 模态分析

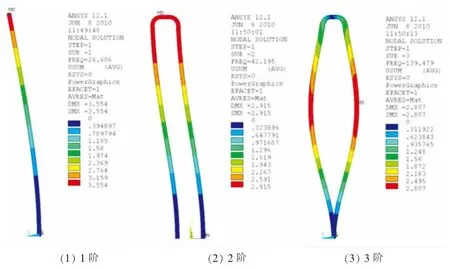
首先给出U型管的前6阶模态频率和模态响应，如表2和图3所示。

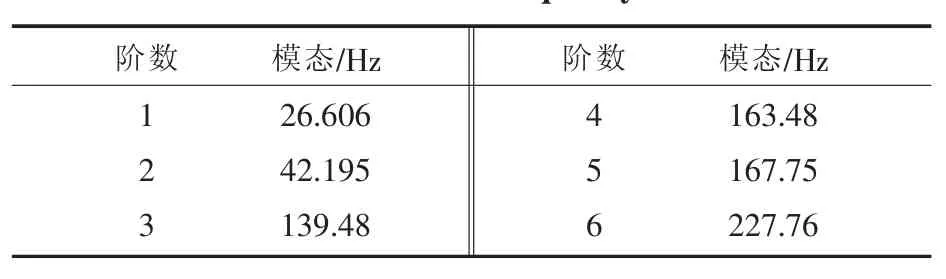
表2 U型管的前六阶固有频率Tab.2 First six mode frequency of U-tube

通过对图3进行观察，可以发现U型管的前6阶固有模态中，1、3、5阶的振动响应方向为z方向；2、4、6阶的振动响应方向为x方向。

5.2 CFD分析

首先给出流体区域不同高度 （y＝0.25 L，y＝0.5 L，y＝0.75 L，y＝1 L）的平面上，时刻为t＝1.5 s时的压强分布云图，如图4所示。由图4可见，同一时刻，y值不同，压强的分布有所不同，尤其在靠近U型管连接管的区域。说明三维流体流动问题和二维流体流动问题存在一定的差异［5-6］，在将三维流动简化为二维流动问题时必须对结果进行相应的修正。涡量的等值线图如图5所示，其中加框的区域为U型管管壁。

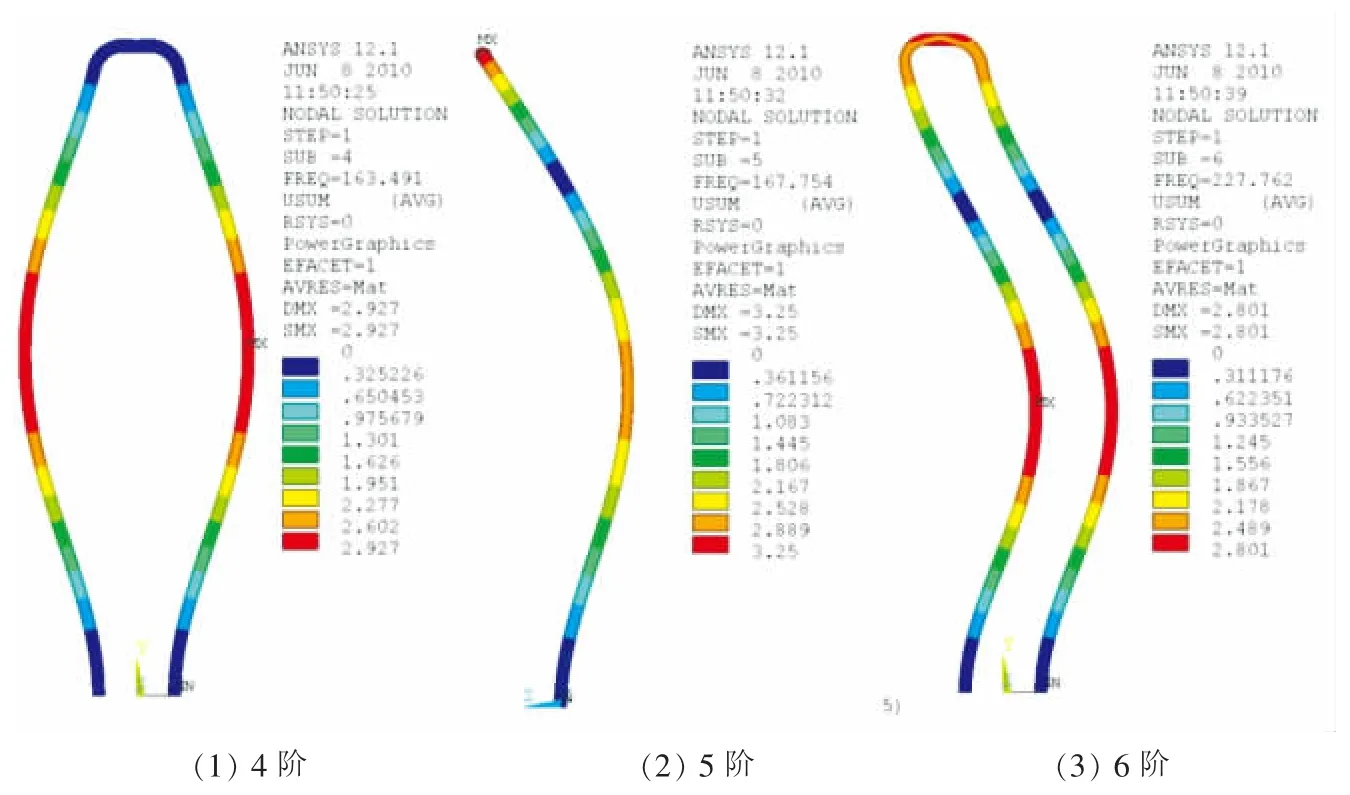
图3 U型管前6阶模态响应Fig.3 First six modal response of U-tube

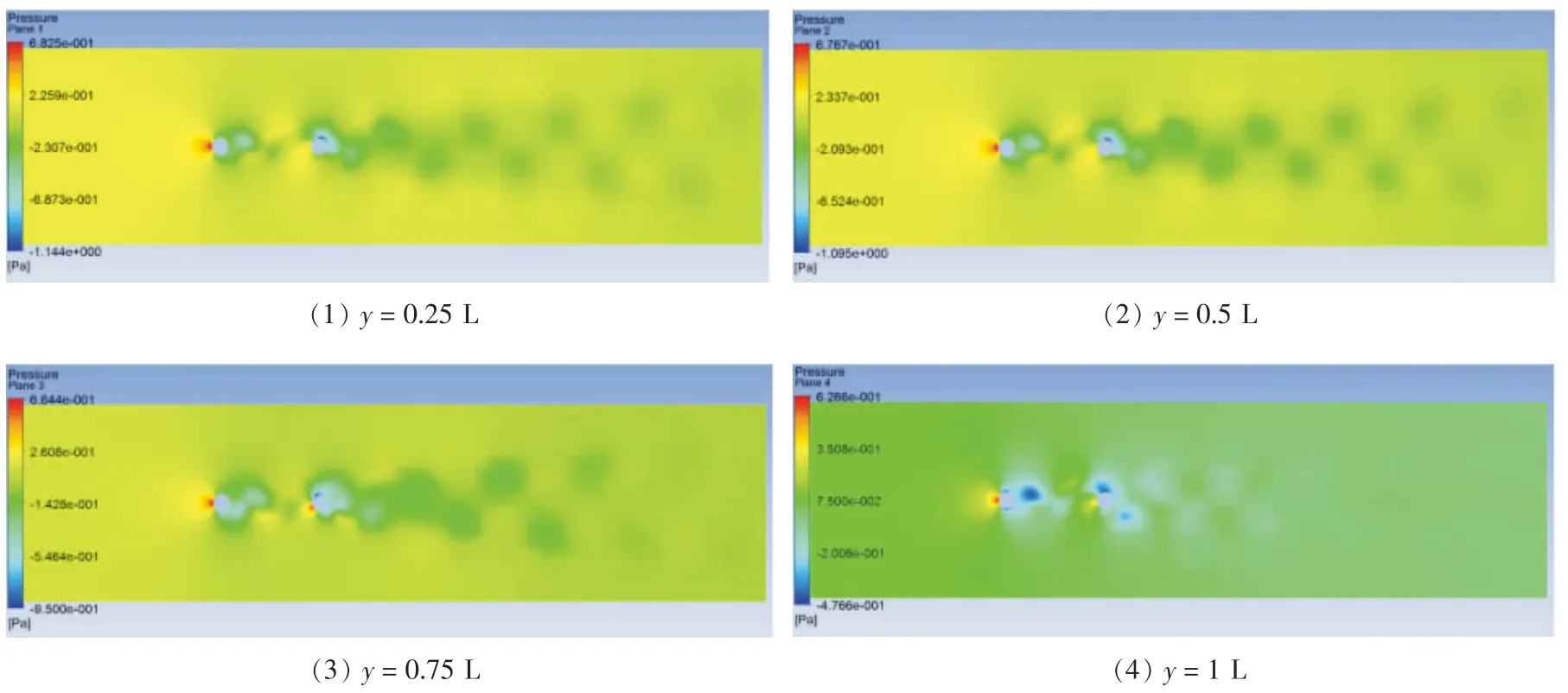
图4 压强分布云图Fig.4 Pressure distribution

从图5中同样可以看出，y值不同涡量的等值线是有所不同的。图6所示为升力系数和阻力系数的时程图，观察0.5～1.5 s稳定时段，可以得出升力系数的变化频率为16.5～17 Hz，阻力系数的变化频率为33～34 Hz，即阻力系数的变化频率为升力系数变化频率的2倍。

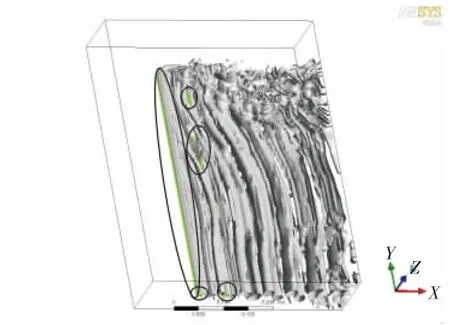
图5 涡量等值线图Fig.5 Isogram of vorticity

5.3 结构分析

下面给出U型管上3个监测点的振动加速度谱线，如图7所示。图7中的数值的点划线分别对应着升力系数或阻力系数的变化频率，虚线分别对应着U型管的1阶或2阶固有频率。对于x方向（即阻力方向）的振动加速度级谱线，在升力系数对应的频率点和2阶固有频率点均是尖峰点，2阶固有频率的振动响应方向是x方向；对于z方向（即阻力方向）的振动加速度级谱线，在阻力系数对应的频率点和1阶固有频率点也均是尖峰点，1阶固有频率的振动方向是z方向。对于其他固有频率点，在谱线上也有相应的反应，但振动幅值突变不明显。通过以上分析说明流体掠过U型管引起的振动成分主要集中在结构的固有频率以及流体升力和阻力变化的频率附近。

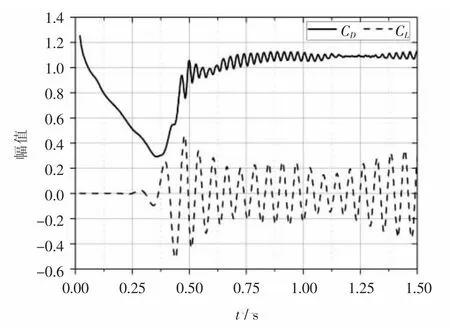
图6 升力、阻力系数时程图Fig.6 Lift and drag coefficients

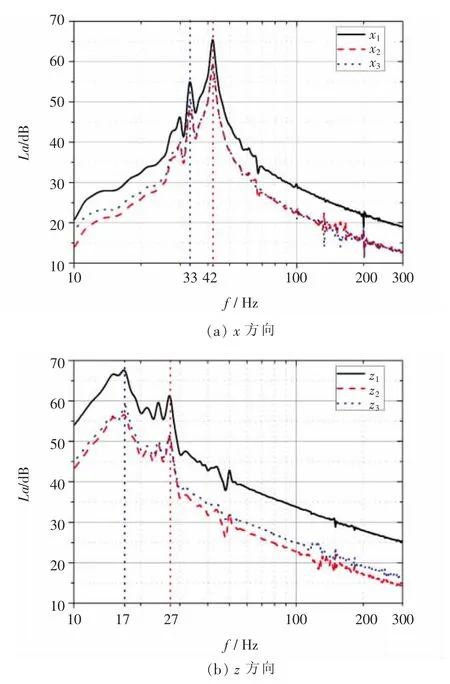
图7 U型管振动加速度级谱线Fig.7 Vibration acceleration of U-tube

图7的数值的点划线分别对应着升力系数或阻力系数的变化频率，虚线分别对应着U型管的1阶或2阶固有频率。对于x方向（即阻力方向）的振动加速度级谱线，在升力系数对应的频率点和2阶固有频率点均是尖峰点，2阶固有频率的振动响应方向是x方向；对于z方向 （即阻力方向）的振动加速度级谱线，在阻力系数对应的频率点和1阶固有频率点也均是尖峰点，1阶固有频率的振动方向是z方向。对于其他固有频率点，在谱线上也有相应的反应，但振动幅值突变不明显。通过以上分析说明，流体掠过U型管引起的振动成分主要集中在结构的固有频率以及流体升力和阻力变化的频率附近。

6 结论

本文通过对换热器内单根U型管的流固耦合分析，得到了管外流体的流动形态以及U型管振动的加速度级谱线，并总结了以下结论：

1）二维流动问题和三维流动问题大体的形态是一样的，但在深度方向存在一定的差异，在用二维模型代替三维模型进行简化时要进行相应的修正。

2）流体引起的结构振动的振动频率成分主要集中在结构本身的固有频率和流体升力和阻力变化频率附近。在对换热器管束进行设计时，要使管束的固有频率远离流体升力系数和阻力系数的变化频率，避免共振。

［1］SCWARZ G W.Preventing vibration in Shell－and－tube heat exchange［J］.Chemical Engineering，1976，83（15），134－140.

［2］钱颂文，袁明可.换热器振动破坏、振动应力及改进措施［J］.石油化工设备技术，1982（6）：1－6.

［3］钱颂文，吴家声，曾文明.换热器流体诱导振动基础［M］.武汉：华中工学院出版社，1988.

［4］PETTIGREWA M J，TAYLORB C E.Vibration analysis of shell－and－tube heat exchangers：an overview－Part 1：flow，damping，fluidelastic instability［J］.Journal of Fluids and Structures，2003，18（5）：469－483.

［5］王福军.计算流体动力学分析——CFD软件原理与应用［M］.北京：清华大学出版社，2004.

［6］王亚玲，刘应中，缪国平.圆柱绕流的三维数值模拟［J］.上海交通大学学报，2001，35（10）：1464－1469.

Numerical Simulation of Fluid－Induced Vibration in U－Tube Based on FSI

Pang Tian－zhao1Guo Wei1Sheng Yuan－ping2Guo Tao3
1 Naval Military Representative Office in No.431 Plant，Huludao 125004，China 2 Shenyang Military Representative Department，Naval Armament Department of PLAN，Shenyang 110003，China 3 School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

Fluid-induced vibration of U－tube was analyzed by two－way FSI with ANSYS and CFX software.Large eddy simulation model and structural vibration model were built，obtaining the time－dependent lift coefficient，drag coefficient of the fluid flowing past U－tube and the vibration acceleration level of U－tube.The results show the primary frequency of structure vibration is near to the frequencies of left and drag and the natural frequencies of U－tube.Numerical simulation results can support the engineering practice.

fluid－induced vibration；fluid-structure interaction；large eddy simulation

TB532

：A

：1673－3185（2011）04－29－05

2010-06-23

国家自然科学基金资助（10702022）

庞天照（1983－），男，助理工程师。研究方向：机械制造与自动控制。E-mail：2002381036＠163.com

郭 伟（1983－），男，助理工程师。研究方向：机械制造与自动控制。E-mail：513730179＠qq.com

10.3969/j.issn.1673-3185.2011.04.006