成形磨齿砂轮截面廓形建模及修形

吴锋超,邓效忠,苏建新

(河南科技大学机电工程学院,河南洛阳 471003)

0 前言

成形法磨齿是利用成形砂轮磨削齿轮的渐开线齿形,齿轮的渐开线齿形主要由砂轮廓形保证。在磨削直齿圆柱齿轮时,砂轮的轴线垂直于齿轮的轴线,砂轮轴向截形的对称线和齿轮齿槽的对称线相重合,砂轮的轴向截形就相当于齿轮齿槽的端面截形[1]。以前的砂轮截面廓形是按齿槽的公称尺寸设计,利用单面磨削方法获得齿侧间隙。这样砂轮及工件的受力不对称,不利于磨齿精度的提高,操作也繁琐。本文按照齿轮齿槽的实际尺寸设计砂轮截面廓形,砂轮及工件的受力对称,有利于磨齿精度的提高,操作相对简单,磨削效率和自动化程度高。

一般数控系统只有直线和圆弧插补功能,因此,对渐开线廓形曲线进行修形,需要进行数值处理。即用一系列的直线段或圆弧去逼近渐开线,并计算出这些小段直线或圆弧的连结点坐标,即节点坐标。圆弧逼近程序段少、误差小、而且刀具轨迹相对圆滑[2-4]。本文在 VC++环境下编写程序计算渐开线的节点及其圆心和半径,并生成NC加工代码。

1 公法线长度偏差与基圆齿槽半角之间的关系

1.1 砂轮模型建立的理论依据

在加工齿轮时常用公法线长度来控制齿厚,以达到控制侧隙的目的。在齿轮的工作图中,常看到的也是公法线长度以及上下偏差。假设公法线的长度为L,上偏差为△mL,下偏差为△ML,在(L-△mL)与(L-△ML)之间,只要给一个偏差值,就对应一个砂轮截面模型。

1.2 基圆齿槽半角

所谓基圆齿槽半角,就是基圆齿槽所夹的中心角的一半,如图1所示。标准直齿圆柱齿轮中,分度圆处的渐开角为[5-6]:

由于分圆齿槽半角等于π/(2z),故基圆齿槽半角为:

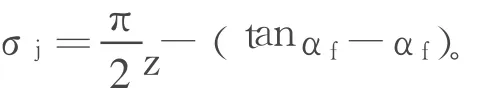
对于变位齿轮,基圆齿槽半角为:

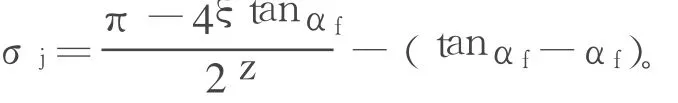
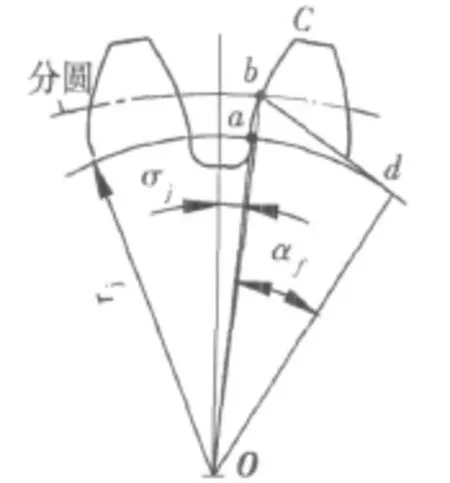
图1 基圆齿槽半角

以上公式中,z为齿数;αf为分圆压力角;ξ为变位系数。

1.3 公法线长度偏差与基圆齿槽半角的关系

对于标准直齿轮:σ′j=(tanαf-αf)+

对于变位直齿轮:σ′j=-(tanαf-αf)+

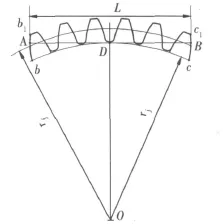
图2 公法线长度偏差与基圆齿槽半角关系

这里用 σ′j表示改变后的基圆齿槽半角,以区别于公称尺寸的基圆齿槽半角 σj。

2 砂轮截面廓形方程的建立

在图3中,以齿轮中心为座标原点 O,通过齿槽对称线作OY座标轴线。设齿槽右侧渐开线在基圆上的起点为 a点。渐开线齿形的极坐标表达式为:

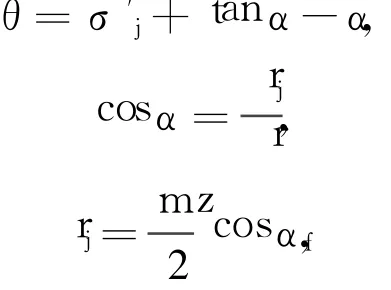
式中,α为压力角;θ为极角;r为极径。

渐开线的直角坐标表达式为:

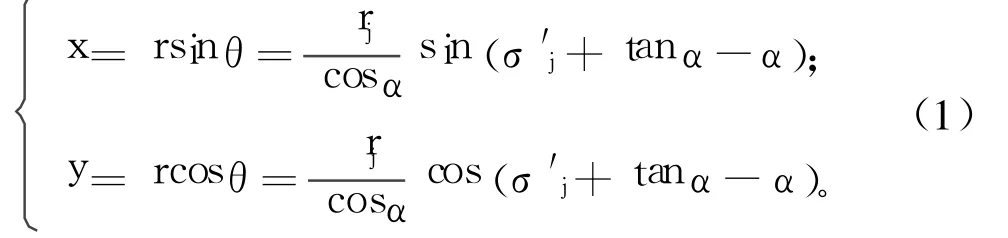
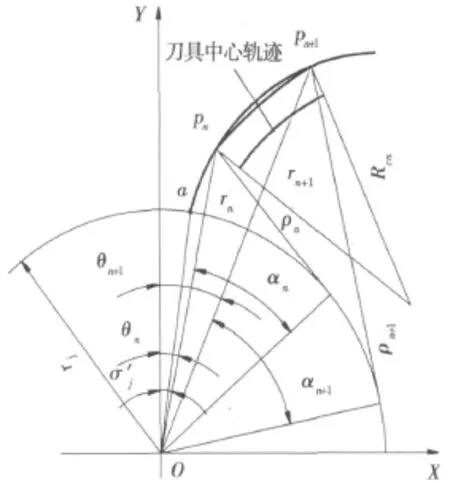
图3 渐开线齿形坐标及节点划分

由于左侧齿廓与右侧齿廓关于 y轴对称,左侧的渐开线齿形方程,只需把上面方程中的 x取负值即可,齿根圆用直线y=r根代替。

3 圆弧逼近曲线的节点计算

3.1 渐开线上节点的离散

如图3所示,设圆弧逼近允差为 ε,根据文献[7],相邻两节点 pn与 pn+1曲率半径之间的关系为:

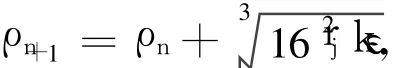
式中,k为放大系数,可在 6～9范围内选取。

逼近圆弧半径为:

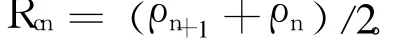
知道了划分节点的曲率半径后,就很容易求出节点处渐开线的压力角 α。

3.2 刀具圆弧中心轨迹的推导

成形砂轮廓形是靠金刚石滚轮的外圆与端面之间的圆弧倒角(半径为R)来进行修整的,圆弧倒角的中心运动轨迹曲线与砂轮轴截面廓形曲线是一对间距为 R的等距曲线。所以,要修整出正确的成形砂轮廓形,还需要利用等距曲线推导出金刚石滚轮圆弧中心的运动轨迹。这对于无刀具半径自动补偿功能的机床尤为重要。

若已知曲线的参数方程为x=x(t)、y=y(t),则间距为a的内等距曲线方程为[8]:

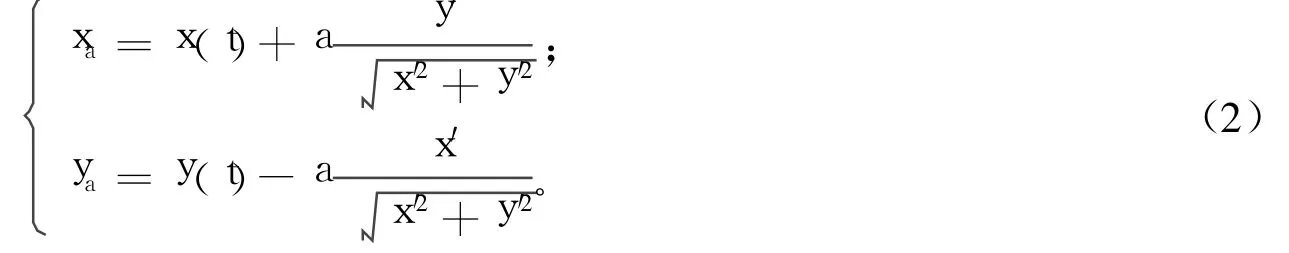
由于成形砂轮廓形凹向砂轮方向,所求刀具中心运动轨迹曲线在砂轮廓形法线的正方向,所以所求等距曲线是成形砂轮廓形的内等距曲线。分别将式(1)中x、y对α求导,并代入式(2)可得间距为 R的等距曲线参数方程

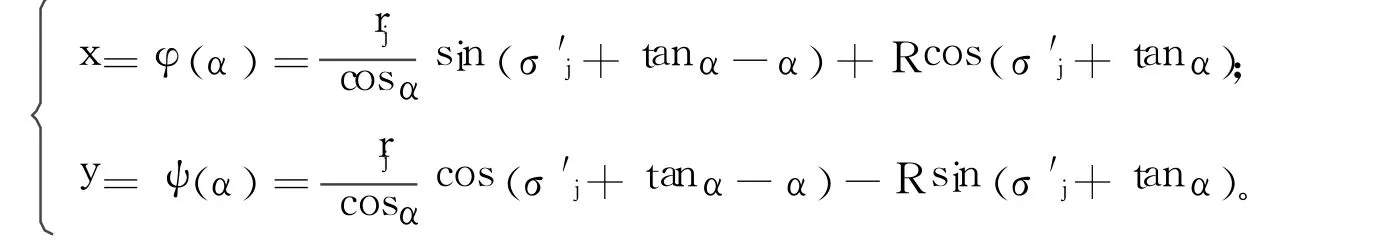
金刚石滚轮圆弧中心轨迹与渐开线的逼近圆弧是等距圆弧,其圆心相同半径相差 R。

3.3 计算机实现圆弧逼近节点计算和NC代码生成

在 VC++开发环境下开发计算程序,该程序主要包括:基本参数输入、生成节点坐标、逼近圆半径、误差值及NC代码。如果最大误差超过逼近允差,应改变放大系数k值重新计算。

现以齿数z=20,模数m=5,分圆压力角αf=20°的标准圆柱齿轮为例来计算各参数。计算表明:圆弧法逼近渐开线误差极小,逼近精度相当高,而且程序段很少。程序运行后,图形界面如图4所示。图5是生成的NC代码。

图4 程序运行界面

4 结束语

本文所建砂轮截面廓形的数学模型,改进了成形法磨齿时的磨削工艺,实现了砂轮截面廓形的数字化设计,利用程序实现圆弧逼近节点划分,自动生成数控加工代码,方便了数控程序员编程,为成形法磨削圆柱直齿轮提供了参考和借鉴。

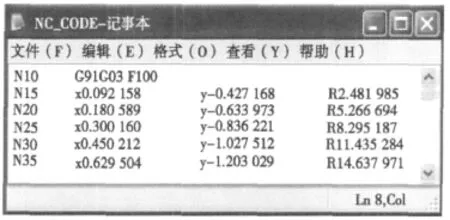
图5 生成的NC代码

[1] 贺红霞,张洛平.基于斜齿圆柱齿轮数控成形磨削方式下的砂轮修形轨迹计算[J].煤矿机械,2004(10):12-14.

[2] 丁克会,席平原,周红斌.参数方程曲线的最优逼近算法及实现[J].机械传动,2008,32(6):57-59.

[3] 王丽萍,孙国防,季绍坤.非圆曲线数控编程的等误差圆弧逼近法及其实现[J].现代制造工程,2006(10):30-32.

[4] 范云霄,马静敏,沈友徽.非圆曲线的等误差圆弧逼近法及刀具轨迹仿真[J].煤矿机械,2004(12):77-78.

[5] 袁哲俊,刘华明,唐宜胜.齿轮刀具设计:上册[M].北京:新时代出版社,1983.

[6] 秦川机床厂“七.二一”工人大学,西安交通大学机制教研室.磨齿工作原理[M].北京:机械工业出版社,1977.

[7] 张彦博.等误差圆弧逼近渐开线的节点计算新方法[J].组合机床与自动化加工技术,2003(4):26-27.

[8] 傅则绍.微分几何与齿轮啮合原理[M].东营:石油大学出版社,1999.