弧齿锥齿轮锥度切削原理与试验

彭宗和,魏冰阳,邓效忠

(河南科技大学机电工程学院,河南洛阳 471003)

0 前言

弧齿锥齿轮广泛应用于航空、航海、车辆、机床等领域。为了保证其啮合质量,凸凹两齿面沿齿高方向、齿长方向曲率需要进行不同的修正,小轮两侧齿面分别在两台机床上,采用两把刀盘分别加工,即固定安装法[1]。该方法尽管切齿精度高,但投入的机床及刀盘数量较多,适用于大批量生产。格利森公司早期设计制造了用于小轮粗切的锥度切削机床[2-3],但由于机械结构复杂,调整费时,没能够得到应用。伴随着全数控铣齿机的出现,为弧齿锥齿轮锥度切削提供了可行性。本文基于微分几何默尼埃定理,介绍了弧齿锥齿轮的锥度切削原理,建立了锥度切削的数学模型[4],利用局部综合法分析了小轮实现锥度切削的条件,最后进行了小轮锥度切削加工试验。

1 弧齿锥齿轮锥度切削的原理

1.1 锥度切削的理论基础

图1 刀盘坐标系

曲面在不同方向上的弯曲程度是不同的,如果想描述曲面在已知点邻近的弯曲性时,需要用曲面上过该点的不同的曲线的曲率来进行描述。梅尼埃定理[5]几何意义就是,曲面曲线(C)在给定点P的曲率中心就是与曲线(C)具有共同切线的法截线(C0)上同一个点P的曲率中心C0在曲线(C)的密切平面上的投影。弧齿锥齿轮的铣刀盘为一旋转锥面(见图1),锥面半顶角,即刀盘压力角为 α。具体到该刀盘锥面上,就是过P点的横切面是一个半径为r的圆,过P点的法截线在该处的曲率半径为 rn。显然,两条曲线之间的夹角等于刀盘压力角 α。则两条曲线在P点的曲率半径之间的关系为

或写为

式中,k为曲线(C)在P点的曲率;kn为曲线(C)在P点的法曲率。

由上式可以看出:当刀盘的回转半径 r一定时,该点处的法曲率 kn决定于刀盘的压力角 α。这样尽管刀盘半径 r一定,但仍可以通过改变刀盘压力角 α,来满足其对刀盘法曲率的要求[6]。

1.2 锥度切削的原理

因弧齿锥齿轮的齿底的宽度不等,总是带有一定锥度,所以两侧齿面要分别进行加工。但数控铣齿机可以在摇台往上运动时加工一个侧齿面,然后自动改变机床和刀盘的位置,在摇台往下运动时加工另一侧面,实现如图2所示的锥度切削。这种方法省去了机床的空回程,并且能像固定安装法[7]一样保证两侧相同的啮合质量。锥度切削的产形轮刀盘与双面法切齿产形轮刀盘相似,刀盘均需交替安装内外刀片,刀盘安装内刀片和外刀片根据锥度切削的方式不同而有所不同。由于数控铣齿机加工程序通过编程实现,加工参数可适时转换,所以在同一台机床上只需一次装夹,即可通过锥度切削实现齿轮的双侧齿面加工。

2 实现锥度切削的条件

图2 弧齿轮锥齿轮锥度切削原理

要进行锥度切削,刀盘的刀尖半径必须满足一定的条件,具体要求是弧齿锥齿轮小轮切削时外刀成形半径 rp1和内刀成形的半径 rp2的差值要在合理的范围内,即要求内、外刀组合图后,能进入同一齿槽,如图2所示。内、外刀尖半径须满足以下条件:

式中 ε为齿轮根部最窄齿底槽宽。

由梅尼埃定理可知在式(1)中,α角的变化与曲面曲率的大小关系着法平面上曲率的变化。当曲面曲率成为定值时,法平面上曲率的变化就与 α角的变化成了唯一确定的关系了。而刀盘半径是一个关于刀具压力角的函数表达式rcp=f(α),因此,只要调整好参数α的值,就可以使刀盘的刀尖半径满足锥度切削所要求的条件。弧齿锥齿轮的锥度切削原理适用于大轮和小轮的切削。本文以小轮为例。

3 加工参数的确定与试验

3.1 确定小轮加工参数

利用局部综合法[8],由大、小轮两齿面的主曲率、主方向之间关系可求得小轮的刀尖半径为

式中,rcp为小轮刀尖半径;α1为刀具齿形角;ku为参考点处的纵向主曲率;ucp为刀盘齿形线性坐标。

把上式对 α求微分,可得刀尖半径随压力角变化之间的关系:

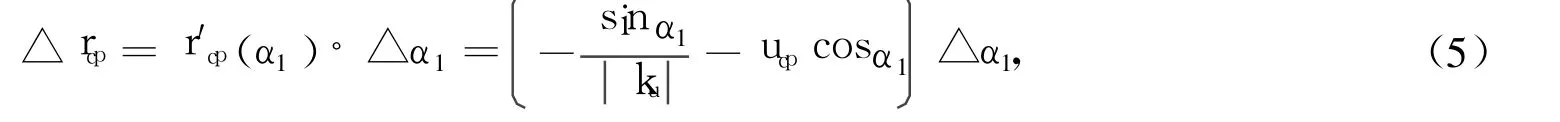
式中括号内项目可视为常数。这样△rcp与△α1呈线性关系,因此,很容易通过选择适当的压力角使刀尖半径 rcp满足锥度切削的条件要求。机床其他加工参数的确定参考文献[2]和文献[8]。

3.2 实例分析

本例以大轮右旋、小轮左旋的弧齿锥齿轮副为例进行分析,仅计算小轮加工参数[9],大轮加工参数与格里森方法相同,不再赘述。表1是弧齿锥齿轮的参数,利用Matlab编制了弧齿锥齿轮加工参数计算程序,计算结果如表2所示。

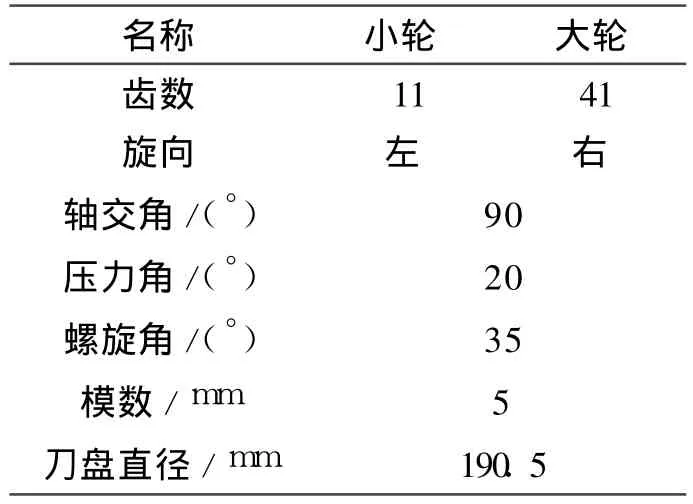
表1 齿轮参数

表2 小轮加工参数

由计算程序算出的齿轮根部最窄齿底槽宽为ε=1.553 mm,而切削小轮的内刀刀尖 rp1=96.011 mm,外刀刀尖半径rp2=95.104mm,该条件满足锥度切削条件公式(3)。

3.3 小轮锥度切削试验

利用Matlab编写的齿面点计算程序可以准确的计算出理论齿面点的三维坐标,利用Pro/E三维造型软件,导入计算出的齿面点进行小轮三维造型,如图3所示。

在小轮进行锥度切削试验验证时,只要刀盘在切削齿轮的凸、凹面时,内外刀与轮坯以及加工好的轮齿不出现干涉、过切、根切等现象,与配对的大轮进行滚检,接触印痕良好,即可说明弧齿锥齿轮锥度切削加工方法可行性。

图3 小轮三维造型

本试验在数控化改造后的GH 35C铣齿机上进行,GH35C锥齿轮铣齿机锥度切削时,刀盘同时加装内切刀片和外切刀片,但需由手工调整机床变换凹、凸加工面。加工时,机床先按小轮凸面加工参数调整,刀具从小端向大端切削展成出凸面(见图4)。当铣削完凸面后,机床再按小轮凹面加工参数调整,摇台和轮坯同时反向旋转,从大端向小端切削展成加工出凹面。由于所使用的刀盘同时加装了内、外刀片,因此在加工过程中,只要刀齿与已加工面没有发生过切、根切或干涉情况就可以认为锥度切削加工方法是可行。

为了易于观察,在切小轮凹面时,先在加工好的小轮凸面上涂上红丹粉,从试验情况看,涂在小轮凸面上的红丹粉完好无损,说明在加工凹面时,刀齿与凸面没有发生干涉。大轮切削采用相似方法进行切削加工,如图5所示。

大、小轮锥度切削完成后,放在 Y9950型锥齿轮滚动检查机上对齿面接触区进行滚动检查[10],大轮滚检印痕如图6、图7所示。从图中可以清晰的看出所得到的接触印痕都是从齿轮的齿顶延伸向小端的齿根。

因此,无论是从加工完后的小轮与仿真小轮进行对比,还是从切削后接触印痕观察,都说明弧齿锥齿轮锥度切削条件的加工参数是正确的,弧齿锥齿轮锥度切削加工方法是可行的。

4 结论

介绍了弧齿锥齿轮锥度切削的加工方法和切齿原理。根据局部综合法建立了实现锥度切削加工的条件,通过锥度切削与滚检证明了弧齿锥齿轮锥度切削的可行性,为推广弧齿锥齿轮锥度切削在数控铣齿机上的应用奠定了理论和实验基础。

[1] 北京齿轮厂.螺旋锥齿轮[M].北京:科学出版社,1974.

[2] 曾韬.螺旋锥齿轮设计与加工[M].哈尔滨:哈尔滨工业大学出版社,1989.

[3] 聂帅强.弧齿锥齿轮小轮的锥度切削与仿真[J].机械传动,2010,34(2):11-16.

[4] 张学伟,葛江华,徐克生.基于Pro/E的3D齿轮模型自动设计[J].林业机械与木工设备,2002,30(7):16-18.

[5] 梅向明,黄敬之.微分几何[M].北京:高等教育出版社,2003.

[6] 段振云,王玉石.法向圆弧锥齿轮加工干涉研究[J].制造技术与机床,2007(9):86-90.

[7] 李学军,朱萍玉,武良臣,等.弧齿锥齿轮铣齿机切削系统时序辨识[J].振动测试与诊断,2002,22(4):283-286.

[8] Litvin F L,Fuentes A.Gear Geometry and App lied Theory[M].2ed.Cambridge:Cambridge University Press,2004.

[9] 曹雪梅,方宗德,张金良,等.弧齿锥齿轮小轮加工参数的分析与设计[J].中国机械工程,2007,18(13):1584-1587.

[10] 李君.锥齿轮传动质量动态综合检测分析系统的研究 [D].重庆:重庆大学,2005.