燃气自由射流的正格式数值模拟

朱孙科，陈二云，马大为，乐贵高

(1.南京理工大学机械工程学院，江苏 南京 210094;2.上海理工大学动力学院，上海 200093)

0 引言

在火箭导弹、航空航天等军事工程技术领域都会涉及到燃气射流问题，由于射流实验受测试设备限制且费用高昂，不能提供较详细的流场细节，高分辨率的数值格式能够捕捉到燃气射流复杂流场的波系结构，数值模拟是研究燃气射流的有效手段。

目前，模拟此类流动的数值格式主要有TVD、NND、ENO和间断有限元等［1-4］。20世纪 90年代末，Liu等［5-6］提出了一种求解双曲守恒律的时间和空间均具有二阶精度的正格式，其数值通量由一个采用中心差分格式的数值通量和一个包含弱耗散和强耗散的上风格式数值通量组成，时间上利用Runge-Kutta方法进行离散。该格式构造过程简单，计算经济性好，是一种性能优良的计算格式。

本文在Liu等人工作的基础上［5-6］，将双曲守恒方程的正格式推广到轴对称Euler方程的求解，并将其应用于燃气自由射流的数值模拟。计算结果与实验照片反映的流动特征基本吻合，与高精度、高分辨率间断有限元方法的计算结果相当，马赫盘的位置与实验测量结果误差较小，表明该方法具有较强的激波捕捉能力。

1 控制方程和离散方法

1.1 控制方程

在忽略粘性和热传导效应的假设下，轴对称流动的Euler方程组的守恒形式为:

其中:Ω∈R2，T 是时间变量;U=［ρ，ρu，ρv，E］T;F(U)=［ρu，ρu2+p，ρuv，(E+p)u］T;G(U)=［ρv，ρuv，ρv2+p，(E+p)v］T;S(U)=(- ρv/y)［1，u，v，(E+p)/ρ］T;ρ是密度;u和v分别对应于x和y方向的速度分量;p是压强;E=ρe+ρ(u2+v2)/2，表示单位体积的总能量;e是单位质量的内能，对于理想气体，状态方程为p=(γ-1)ρe;γ 是比热比。

1.2 空间离散

采用正格式方法对控制方程式(1)进行离散，得到如下轴对称Euler方程组的半离散有限差分方程:

其中，Δx和Δy分别为x和y方向上的空间步长。以通量Fi+1/2，j为例，正格式数值通量的构造过程如下。

1.2.1 弱耗散格式构造

将式(2)中的数值通量Fi+1/2，j采用一个中心差分通量和一个上风通量组合而成，引入限制器L0=R diag(φ0(θk))R-1，限制器函数 φ0(θ)满足［7］:

可以构造如下的数值通量:

这里|˚A|是A=▽F的模，它等于R|Λ|R-1，其中|Λ|=diag(|λk|)。

这样可以得到数值通量的如下弱耗散格式:

1.2.2 强耗散格式构造

若A=▽F的模|˙A|=R diag(μk)R-1，这里对角矩阵diag(μk)≥|Λ|。引入限制器 L1=R diag(φ1(θk))R-1，其中，φ1(θ)是 minmod 限制器函数满足［8］:

可以进一步得到数值通量的如下强耗散格式:

1.2.3 正格式数值通量

将以上的弱耗散格式(4)和强耗散格式(6)合并，可以构造如下的正格式数值通量:

1.3 时间离散

为了与空间精度匹配，时间离散采用二阶精度的Runge-Kutta 法［9-10］，即:

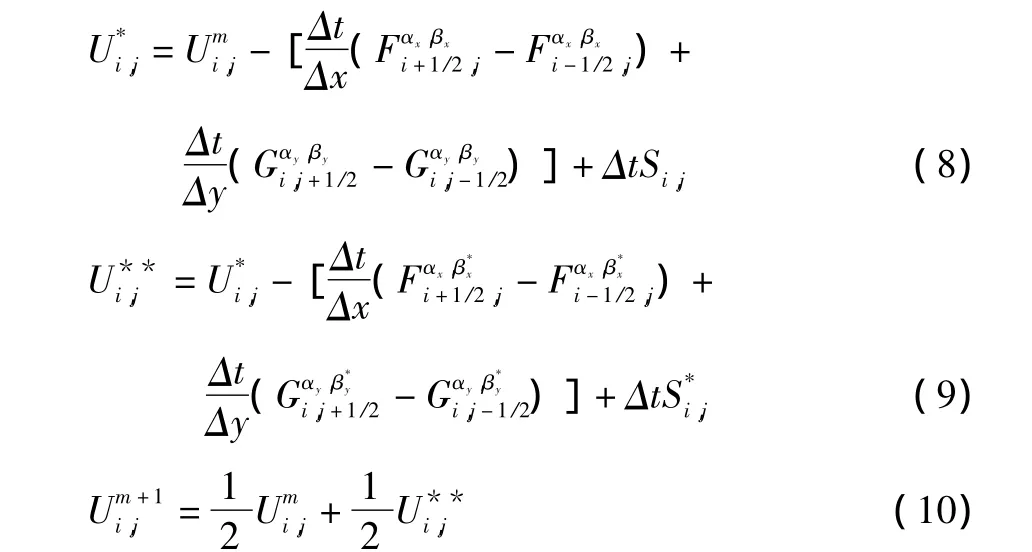
2 计算结果与分析

通过喷管射流任意子午面截得的一半区域如图1所示，计算区域取为［-1∶11］×［0∶4］，轴向距离为12de，径向取4de，其中de为喷口直径，计算网格为Δx=1/20，Δy=1/40。喷流流动参数和外流动参数如表1所示，表中下标“j”表示喷管出口流动参数，“∞”表示外流流动参数。喷流中心轴AB、喷管固壁表面EF和FG采用镜面反射边界条件，喷管出口边界GH采用表1所示的射流条件，下游边界BC采用外推，上游边界DE和外边界CD采用静止大气条件，初场赋予静止大气条件，在t=0时刻喷管出口突然喷出射流。

图1 计算区域Fig.1 Calculation domain

表1 喷流流动参数Table1 Parameters of fluid flow

图2给出了工况1在某时刻的密度和压力等值线分布，从图中可以看到，射流的流场结构类似钻石状，马赫盘略有呈现，入射激波、反射激波、马赫盘等构成的波胞交替产生，由喷管喷出的燃气射流射入压力更低的大气环境，形成的膨胀波使压力能够逐渐过渡到静止大气条件，膨胀波穿过射流传播并在射流边界处被反射回喷流，这种反射过程在射流下游会多次重复出现，形成准周期性的波胞结构。同时由于喷流与静止大气间的对流作用，流场中产生了接触间断面。另外，由于Euler方程可以看作是高Reynolds数下的近似，因此边界层区域附近将出现Kelvin-Helmholtz不稳定性，越往下游不稳定性越明显。该结果与三阶间断有限元方法的数值结果［4］吻合较好，与相同流动条件下的实验纹影照片［11］所反映的流场结构基本吻合，如图2(c)所示。

图2 工况1等值线分布和纹影照片Fig.2 Contours and schlieren photograph in case 1

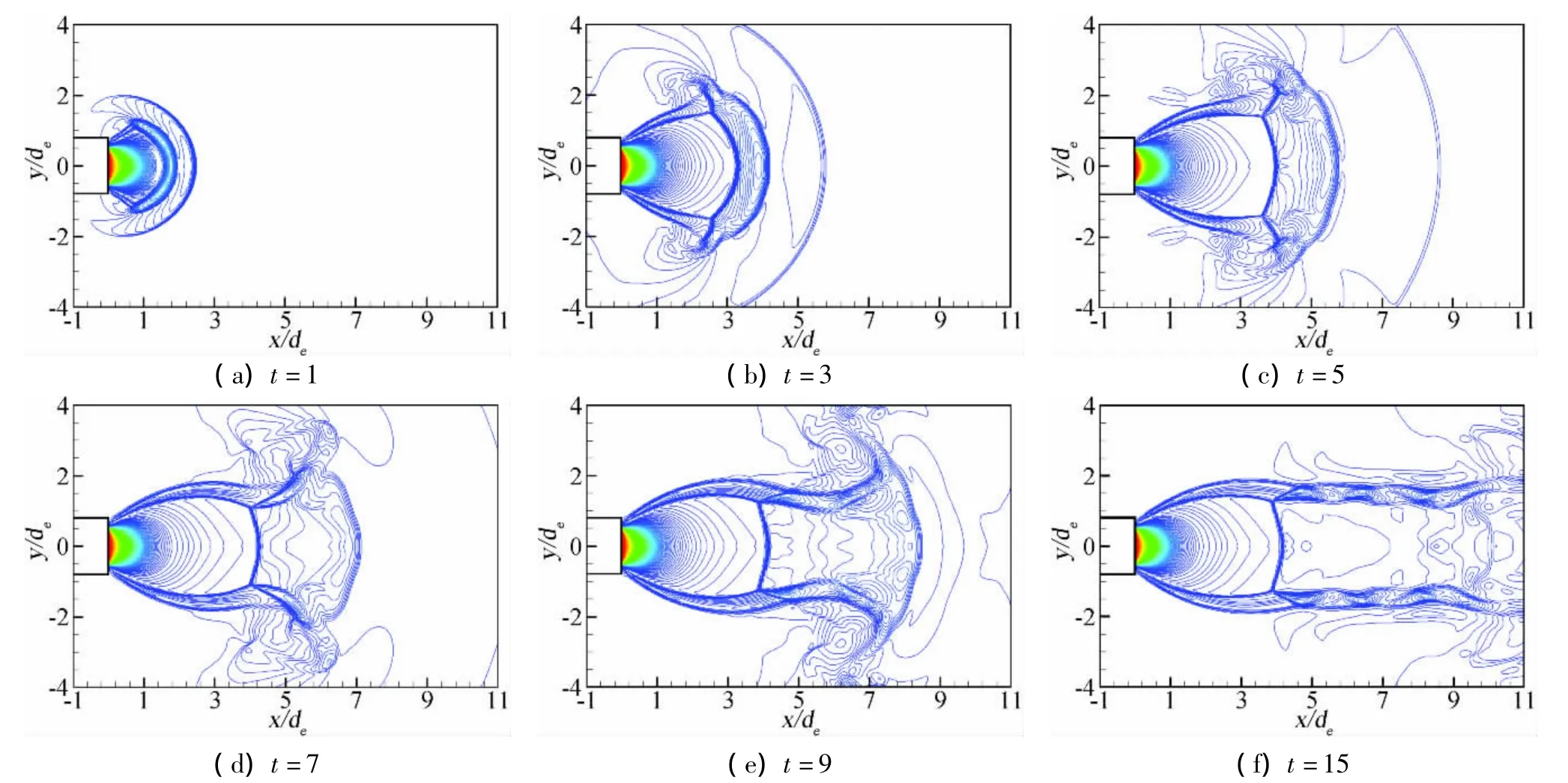
图3 工况2不同时刻密度等值线分布Fig.3 Density contours at different times in case 2

图3给出了工况2下自由射流在不同时刻(时间为无量纲时间)的密度等值线发展过程。观察图3(a)～图3(e)可知，在射流喷出喷管的初期，形成类似球状的不断向外扩张的初始膨胀波，膨胀波在传播过程中遇到射流边界后发生反射，形成的入射激波遇到马赫盘后发生反射，产生反射激波，于是在马赫盘的边缘与入射激波和反射激波交汇，并形成三叉激波，出现三波交点和滑移线。随着时间的推移，流场继续发展，马赫盘上游的流场结构相对稳定，波胞结构并未随时间而改变(如图3(f)所示)，流场趋于稳定，马赫盘下游的流场被滑移线分成内部射流以及由射流边界和滑移线包围的外部射流，并出现明显的Kelvin-Helmholtz不稳定性。与工况1的喷流流场结构相比，由于压力比增加较大，流场中只形成了一个波胞。本文的计算结果第一马赫盘距喷管出口平面的距离为4.07de，与理论预估值［12］(3.972de)相对误差为2.4%，与间断有限元计算值(4.05de)的误差为0.5%，吻合较好。另外，从图3(f)可以看到，第一马赫盘的过渡区间很窄，且三波点清晰可见，表明正格式方法对激波有较强的捕捉能力，得到的马赫盘位置较精确。

图4 工况3等值线分布和纹影照片Fig.4 Contours and schlieren photograph in case 3

图4给出了工况3在某时刻的密度和压力等值线分布，此时流场中形成了比较稳定的马赫盘结构，出现了含膨胀波、桶形激波、反射激波、马赫盘、滑移线、射流边界等非常复杂的流场波系结构，三波点清晰可见，该复杂波系结构与相同流动条件下的实验照片［13］所反映的流动特征符合较好。从图4中可以看到，马赫盘下游区域出现了波动，已有的数值结果和实验均表明，自由射流的流场波动现象是普遍存在的［14］。与工况2对比发现，在保持喷管和马赫数不变的情况下，由于压力的进一步增大，马赫盘出现在射流下游的更远处，并且直径更大。第一马赫盘距喷管出口平面的距离为4.68de，与实验测量值［13］(4.56de)，相对误差为2.6%，与间断有限元计算值(4.6de)的误差为1.7%，吻合较好。

3 结论

将二维正格式发展到轴对称Euler方程组的数值求解，并对三种欠膨胀压力比下的燃气自由射流进行了数值模拟。计算结果与实验照片所反映的流动特征基本吻合，虽然该方法只有二阶精度，但其计算结果可以与三阶精度的间断有限元相比较。利用该方法捕捉到的马赫盘位置，与实验测量值和理论预估值的相对误差小于3%，且得到的燃气射流复杂流场波系结构较清晰，这表明正格式具有较强的激波捕捉能力和较高的分辨率，在燃气自由射流的数值模拟中具有一定的应用前景，可以进一步深入研究。

［1］郑敏，张涵信.无波动、无自由参数的耗散差分格式(NND)在喷流计算中的应用［J］.空气动力学学报，1989，7(3):273-281.

［2］乐贵高，马大为，藏国才.火箭底部流动的TVD数值模拟［J］.弹道学报，1995，7(1):35-40.

［3］徐文灿，黄振宇.高精度ENO格式在射流数值模拟中的应用［J］.空气动力学学报，2001，19(4):401-406.

［4］陈二云，马大为，赵改平，等.燃气自由射流的高精度间断有限元数值模拟［J］.弹道学报，2009，21(1):79-82.

［5］LIU X D，LAX P D.Positive schemes for solving multi-dimensional hyperbolic systems of conservation laws［J］.CFD Journal，1996，5(2):133-156.

［6］LIU X D，LAX P D.Positive schemes for solving multi-dimensional hyperbolic systems of conservation laws II［J］.Journal of Computational Physics，2003，187(2):428-440.

［7］SWEBY P K.High resolution schemes using flux limiters for hyperbolic conservation laws［J］.SIAM Journal on Numerical Analysis，1984，21(5):995-1011.

［8］KURGANOV A，TADMOR E.New high-resolution central schemes for nonlinear conservation laws and convection-dif-fusion equations［J］.Journal of Computational Physics，2000，160(1):241-282.

［9］SHU C W.Total-variation-diminishing time discretizations［J］.SIAM Journal on Scientific and Statistical Computing，1988，9(6):1073-1084.

［10］SHU C W，OSHER S.Efficient implementation of essentially non-oscillatory shock-capturing schemes，II［J］.Journal of Computational Physics，1989，83:32-78.

［11］MATSUDA T，UMEDA Y，ISHII R，et al.Numerical and experimental studies on chocked underexpanded jets［R］.AIAA 87-1378，1987.

［12］张福祥.火箭燃气射流动力学［M］.北京:国防工业出版社，1988.

［13］TESHIMA K，MORIYA T，MORI T.Visualization of a free jet by a laser induced fluoresense method［J］.Journalof the Japan Society for Aeronautical and Space Sciences，1984，32(5):61-64.

［14］ISHII R，UMEDA Y，YUHI M.Numerical analysis of gasparticle two-phase flows［J］.Journal of Fluid Mechanics，1989，203:475-515.