土工格栅加筋界面摩擦特性及界面参数的确定

张大勇 刘博 刘红军

(东北林业大学，哈尔滨，150040)(国家林业局调查规划设计院)(五邑大学)

土工格栅是一种高强度聚合物网格产品，其优点是造价低廉、质量轻、高抗拉强度、高抗腐蚀性、整体连续性好、抗微生物侵蚀好、质地柔软且与土能很好的结合、不直接暴露时抗老化性高。土工格栅对土的加固机理在于格栅与土的相互作用，这种相互作用概括地总结为:①格栅表面与土粒的摩擦作用;②土粒对格栅肋的被动阻抗作用;③格栅上的孔眼对土的“锁定”作用［1］。土工格栅与土的界面作用特性直接决定加筋土工程的稳定性，所以格栅与填料的界面特性是关键的技术指标［2］。国内外许多学者利用直剪试验和拉拔试验研究土工合成材料与填料土的界面作用特性［3－5］。研究结果证明，土工合成材料与填料之间界面特性与土的类型、土的级配、土体含水率等许多因素有关［6－10］。

目前，评价土工格栅的加筋效果主要采用试验和理论计算。理论计算常常采用有限元法，在有限单元法的计算中，把筋土界面设为接触面单元，计算参数选取的准确性直接影响到有限单元法计算的精度。接触面元关键确定切向刚度系数，确定切向刚度系数需要5个参数，这五个参数需要用试验方法来确定，因此，本文重点讨论了5个参数的确定方法，旨在为类似加筋土的研究提供依据。

1 理论基础

在土工格栅加固软土地基的处理中，高模量格栅材料的加入使得土和格栅两种材料之间性质相差悬殊，在一定的受力条件下，两者间的接触面上可能会产生错动滑移或者开裂。

在数值计算过程中，接触面采用无厚度节理单元模拟，用增量形式可表示为:

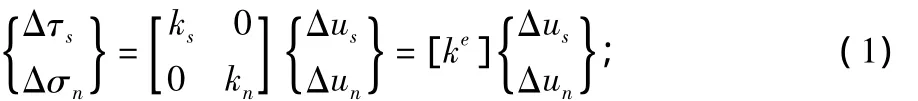
式中:ks为切向刚度系数(单位为kN/m3);kn为法向刚度系数(单位为kN/m3)。

单元长度上的刚度系数ks和kn，表示两片接触面之间要产生单位相对位移所需要的力。对于法向刚度系数kn，为了表征土单元与格栅单元不会在接触面处重叠，在计算中可以取一个极大的数(如1011N/m3)，可使相互嵌入的相对位移小到可以略去不计。通常，计算中更关心接触面上的剪应力。切向刚度系数ks由式(3)可知，共有5个参数，可由筋土界面的摩擦试验确定。

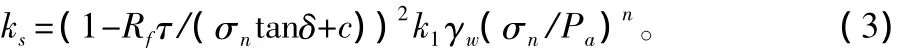
2 试验方法

采用的应变式直剪摩擦试验仪由上下两部分剪切盒组成，上下盒尺寸相同，有效剪切面积为400 cm2。水平剪切力由变速电动机控制的螺旋千斤顶施加，法向压力由螺旋千斤顶施加，水平向剪切位移和剪力由自动采集系统读取。剪切速率采用1 mm/min。

首先，粉质细砂和换填砂砾分别按密度2.08、2.30 g/cm3计算所需用料，用砂砾填平下部剪切盒，并均匀捣实。然后铺一层土工格栅，再将上部剪切盒与下部剪切盒对齐，用螺栓将上下剪切盒联为一体。再将粉质细砂装入上部剪切盒中，捣实找平后放上加压板，连同剪切盒一起放到剪切台上。将连接上下剪切盒的螺栓拔出，各部位充分接触后，施加预定压力后进行剪切。施加的法向应力分别为50、100、150、200 kPa。试验中采用的土工格栅为钢塑格栅，网孔尺寸为15 cm×15 cm，经拉伸试验确定E=2.45 MN/m。

3 结果与分析

图1为不同法向压力作用下，筋土界面的剪应力与剪切位移的关系曲线。由曲线的展布形态可知，加筋界面的抗剪强度随着法向应力的增加而增大，相对的剪切位移小于5 mm时，剪应力增加的较快。

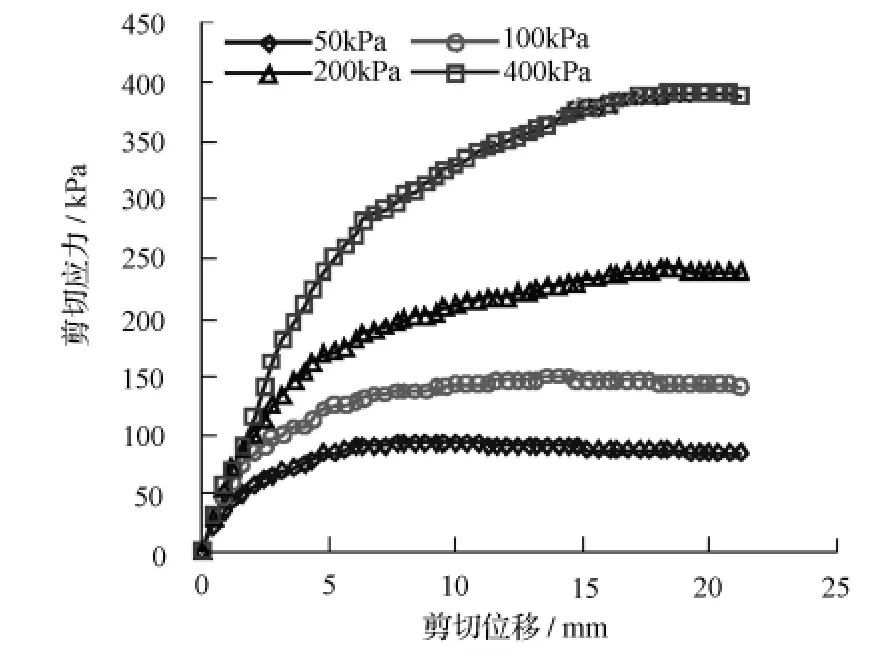
图1 不同法向压力作用下剪应力与剪切位移的关系

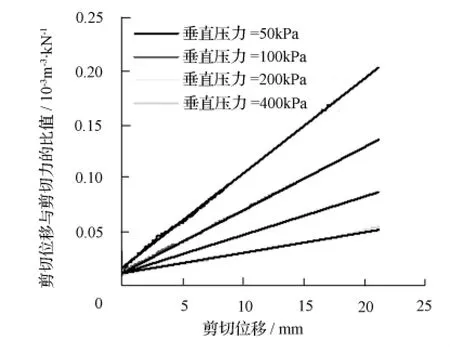
图2 不同法向压力作用下剪切位移和剪应力的比值与剪切位移的关系

对于切向刚度系数ks，根据土与土工格栅接触面上的摩擦试验，如图1所示实测的试验结果，剪应力(τ)与剪切位移(ωs)呈非线性关系，当τ较小时ks较大，τ接近破坏时ks较小。将试验中量测的τ与ωs的数据点绘成图，用类似于表示应力－应变关系非线性的方法将曲线近似表示为双曲线公式。

上式也可以写成

以ωs/τ为纵坐标，以ωs为横坐标，如图2所示，得到截距为a、斜率为b的直线。它们都是剪切面垂直压力σn的函数，各自的方程为:

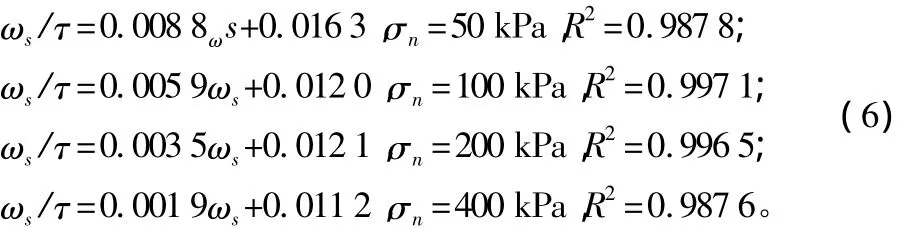
对于某一σn，有

式中:ksi为初始剪切刚度，即图1中曲线在ωs=0处的切线斜率;τu为当ωs→∞时的剪应力，即曲线渐近线的纵坐标。同时可以将ksi和τu与σn的关系分别表示为:

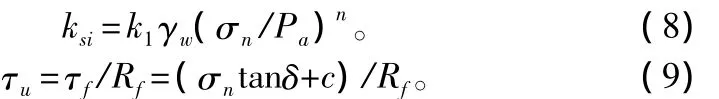
式中:k1、n、Rf为非线性指标;δ为接触面上材料的外摩擦角;γw为水的密度;Pa为大气压力。

将式(7)、(8)、(9)代入式(4)，得:

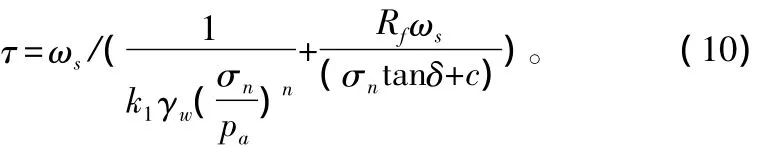
对ωs求偏导，并利用上式将所得方程中的ωs消去，得:

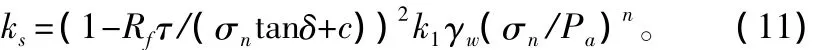
ks就是切线剪切刚度系数，其中所包含的常数k1、n、Rf均可由直剪试验确定。

本文根据直剪试验的结果，利用式τu=1/b，求得每级垂直压力的τu。利用式Rf=τf/τu，求得每级垂直压力的Rf，最后取4级垂直压力的平均值作为ks表达式中的Rf(τf为相对应每级垂直压力下的峰值剪应力，按照JTG E50－2006《公路土工合成材料试验规程》，如果不出现峰值，取相对剪切位移ωs=20 mm对应的剪应力)。

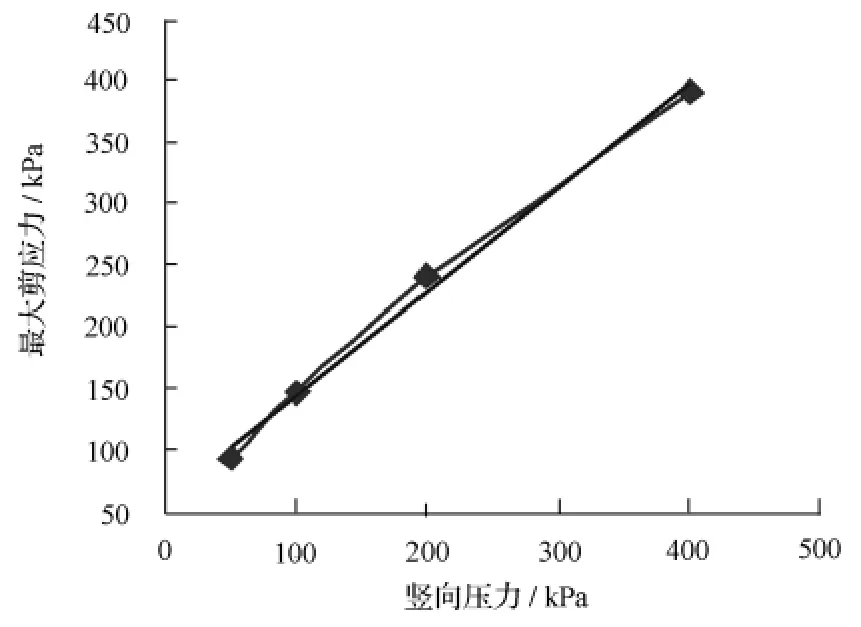
图3 最大剪应力与竖向压力的关系

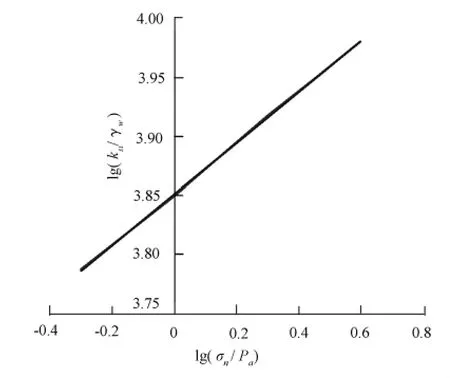
图4 lg(ksi/γw)与lg(σn/Pa)的关系

利用式lg(ksi/γw)=nlg(σn/Pa)+lgk1，以lg(σn/Pa)为横坐标、以lg(ksi/γw)为纵坐标，如图4所示，得到截距为k1，斜率为n。利用图3确定接触面上材料的外摩擦角和黏聚力。根据图3和图4得到的拟合方程分别为式(12)和式(13)。

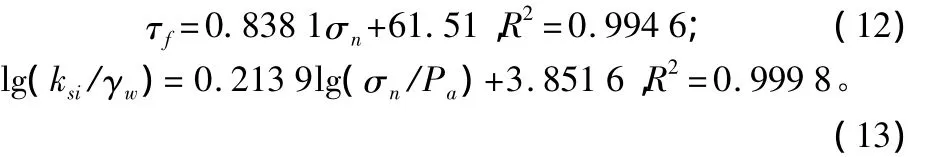
土工格栅铺设在粉质细砂与砂砾之间，根据以上方法确定的接触面元计算参数为:k1=710 6 kN/m3;kn=108kN/m3;δ=40.0°;c=61.51 kPa;Rf=0.83;n=0.21。

4 结论

利用室内加筋界面的直剪试验研究筋土界面的摩擦特性及确定接触面单元参数一种比较可靠的方法，得到了人们的认可。因此，模拟工程中土的实际状态的物理力学性质，进行筋土界面的摩擦直剪试验。根据不同垂直压力下的τ与ωs、ωs/τ与ωs、τf与σn、lg(ksi/γw)与lg(σn/Pa)曲线确定了模型中的5个参数。

在确定模型参数的过程中，采用了对试验数据进行拟合的手段，通过拟合得到的直线方程确定接触面元参数，并利用相关系数验证了试验数据的离散性和可靠性。

［1］吴景海，陈环，王玲娟，等.土工合成材料与土界面作用特性的研究［J］.岩土工程学报，2001，23(1):89－93.

［2］黄培彦，周绪平，赵琛.FRP片材在土木工程中应用的几个关键力学问题［J］.华南理工大学学报:自然科学版，2002，30(11)):101－105.

［3］施有志，马时冬.土工格栅的界面特性试验［J］.岩土力学，2003，24(2):296－299.

［4］Huang P Y，Long Z Q，Lou Y，et al.Experimental study on loadcarrying capacity of carbon fiber-sheet-rein-forced concrete threepoint bending specimen with a V notch［J］.Proc SPIE，2002，4537:95－98.

［5］徐林荣，吕大伟，顾绍付，等.筋土界面参数的拉拔试验过程划分研究［J］.岩土力学，2004，25(5):709－714.

［6］马学宁，杨有海.土工格栅与土界面特性的试验研究［J］.兰州铁道学院学报:自然科学版，2003，22(4):88－90，104.

［7］张文慧，王保田，张福海，等.含水率对经编土工格栅与土界面作用特性的影响［J］.中南公路工程，2007，32(3):24－41.

［8］尹光志，张东明，魏作安，等.土工合成材料与细粒尾矿作用特性的试验研究［J］.岩石力学与工程学报，2004，23(3):426－429.

［9］杨广庆，杨春玲.土工格栅拉拔试验影响因素分析［J］.地下空间，2004，24(1):31－32，63.

［10］刘文白，周健，苏跃宏.风砂土基本性质及其与土工格栅作用试验［J］.中国沙漠，2003，23(6):697－702.