三次样条插值在电弧炉无功补偿中的应用

贾文超， 赵 欣

（1.长春工业大学电气与电子工程学院，吉林长春 130012; 2.国营汉光机械厂，河北邯郸 056028）

0 引 言

电弧炉以其灵活性、可靠性、较快的冶炼速度以及较优的冶炼质量等优势在冶金行业得到了广泛应用。电弧炉工作时，由于电弧长度急剧变化，引起无功急剧波动，导致电网电压的闪变和波动;由于各相电弧电压是独立变化的，三相电弧各自急剧无规则变化，故其三相电流是不对称的，产生负序电流;平均功率因数低于0.75，在发生工作短路时甚至低于0.1[1-2]。由于电弧炉的容量大，是用电大户，导致其所在的电网也存在电压闪变和波动严重、高次谐波多、电网功率因数低的问题，这不仅影响电炉自身的质量，使电耗、电极消耗增大，更危及发配电和大量用户，成为目前电网最主要的公害之一，进行无功补偿是解决以上问题的必要手段。

1 晶闸管可控电抗器的基本原理

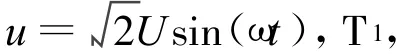
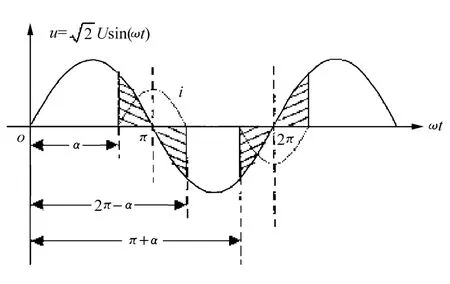
图1 TCR单相电压电流波形图

TCR的基波等效电纳为[4]:

XL——实际电抗值。

我们得到:

对于基波，晶闸管控制的电抗器可看作一个可控的电纳。在反并联晶闸管完全对称的情况下，TCR产生的主要是奇次谐波，在电流系统中容易消除3次谐波，而5，7，11，13等次谐波分量已足够小，所以只需考虑基波电纳[5-6]。TCR中电感电流的导通时间与电感本身无关，仅取决于α。所以无功补偿就在于得到无功量，进而求得补偿电流即可，无功补偿的问题只要精确控制了相位角α，也就控制了电流量，就可以精确地进行无功补偿。另外，TCR的动态响应好是一个独具的优点，也是它被广泛应用的重要原因[7]。

2 样条插值函数

在实际应用中，通常是先得到补偿电纳值，再根据该值，通过解方程组得到触发角的值。由于式（1）为超越方程，在计算机中求解比较困难，故采用函数逼近的方法，根据已知条件，建立相应的函数[8]。因为晶闸管控制角的计算精度直接影响无功补偿的效果，故选择合理的计算方法就比较重要，文中运用三次样条插值法来实现晶闸管控制角的计算。在可控电纳BL（α）与控制角α的关系式（1）中，如果取

则有:

三次样条插值重点是求取弯矩方程，下面介绍弯矩方程:设R（x）在节点a≤x0＜x1＜…＜xn≤b上的二阶导数值为R″（xi）=Mi（i=0，1，…，n），由于R（x）在[xi，xi+1]上是二阶光滑三次多项式，故R″（x）在[xi，xi+1]上是线性连续函数，表示为:

其中，hi=xi+1-xi，对此式两端在区间[xi，xi+1]上求积分两次，并利用R（xi）=fi，R（xi+1）=fi+1可确定积分常数，从而得到样条插值函数:

这里，Mi（i=0，1，…，n）是未知量，但它可利用条件R′（xi-0）=R′（xi+0）（i=1，2，…，n-1）得到关于 M0，M1，…，Mn的方程组，当 x∈[xi，xi+1]时，对R（x）求导得

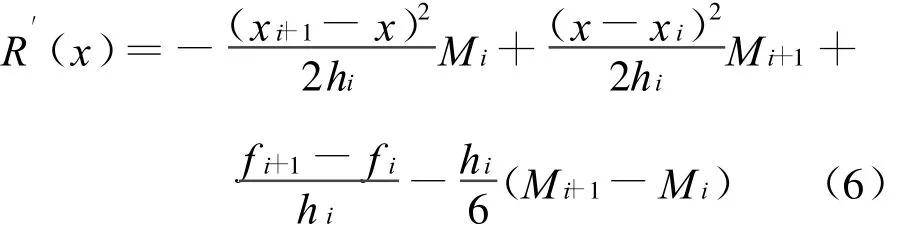
由此可得

当x∈[xi-1，xi]，可得

由R′（xi-0）=R′（xi+0），可得到

其中

式中:f[xi-1，xi，xi+1]——f（x）关于节点xi-1， x，xi+1的二阶差商。

式（9）是含有n+1个未知量M0，M1，…，Mn的（n-1）个方程，再由R′（x0）=f′（x0），R′（xn）=f′（xn）补充两个方程，它们可由式（5）当i=0时及式（6）当i=n时得到，即

矩阵形式表示为

其中

3 计算结果与仿真

其计算结果见表1。

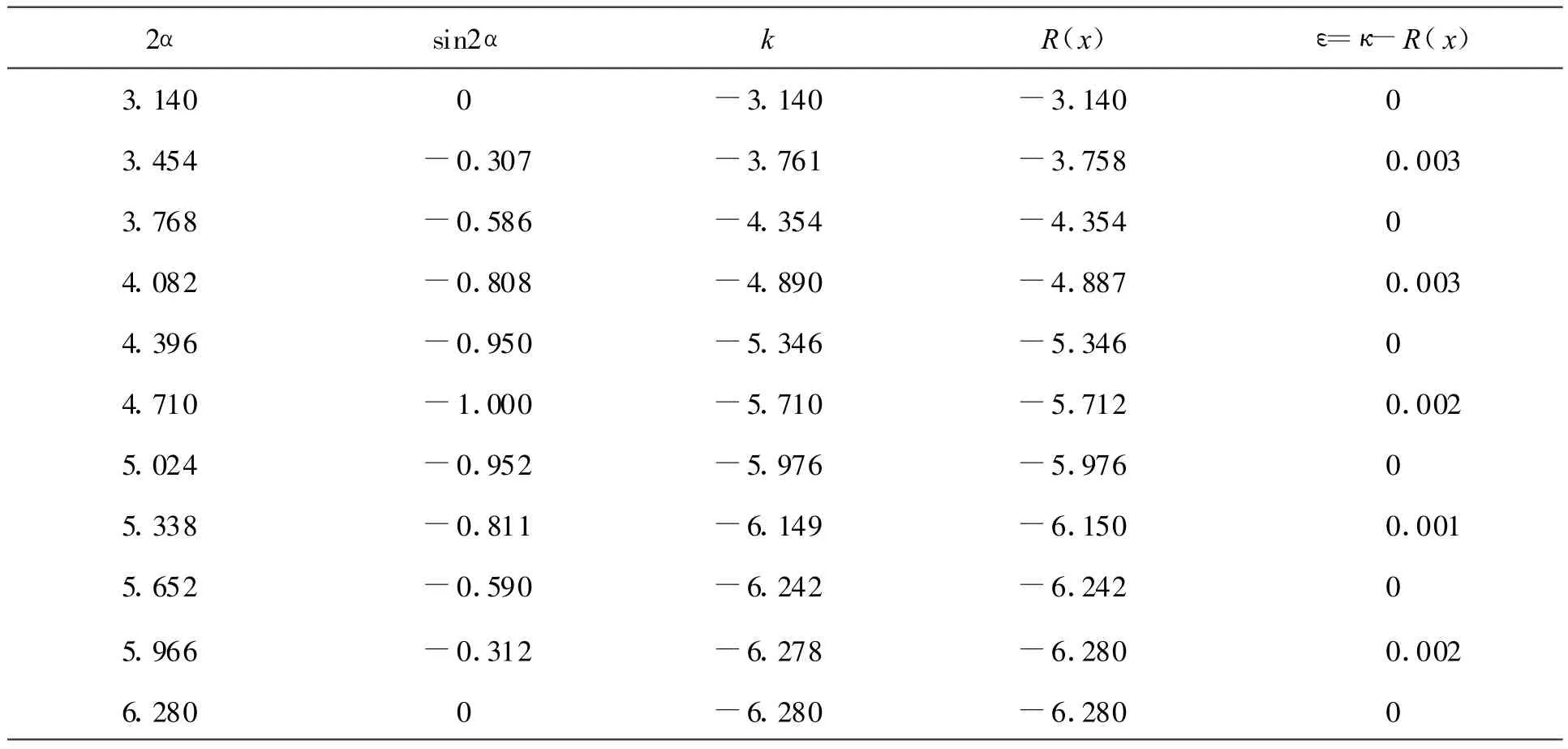
表1 原函数与插值函数对照表

由表1中的计算结果可知，计算误差最大为0.003，完全符合预期的要求。

根据所得插值函数结果，在MATLAB下进行仿真。将原晶闸管触发角函数曲线sinγ-γ=κ和建立的样条插值函数曲线R（x）进行对比，利用plot（x，y）得到拟合图形，如图2所示。

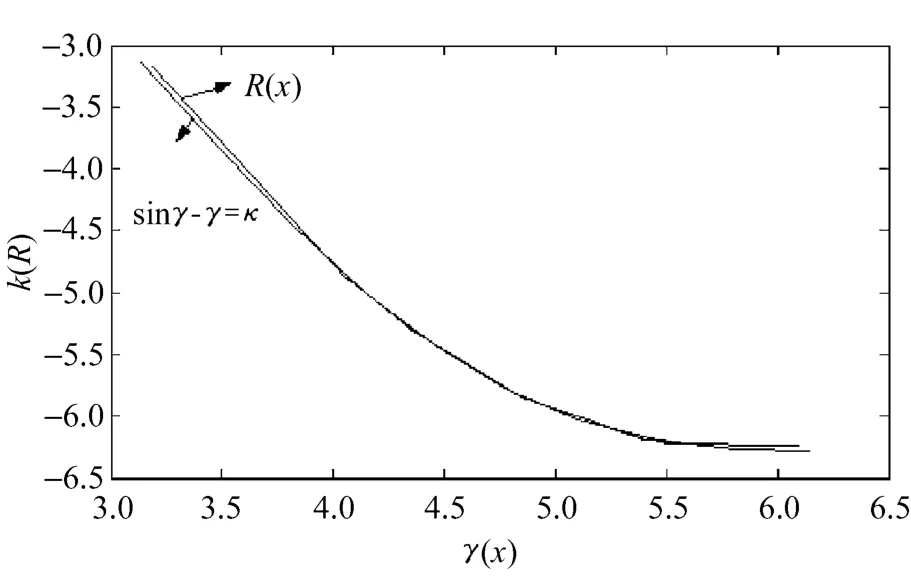
图2 原函数与样条函数对照

4 结 语

阐述了当前无功补偿技术在应用中存在的一些问题，采用晶闸管可控电抗器可以减小损耗，降低冲击电流产生的负面影响，实现节能的目的。由于晶闸管可控电抗器方程不能直接求解，所以采用函数逼近的方法建立起三次样条插值方程，通过计算机仿真表明，该方法原理正确、方案可行。

[1] 张定华，桂卫华，王卫安.大型电弧炉无功补偿与谐波抑制的综合补偿系统[J].电网技术，2008，32（12）:23-29.

[2] 贾文超，宋恩锋.基于PDF的电弧炉电极控制系统[J].长春工业大学学报:自然科学版，2008，29（6）: 684-687.

[3] 方忠民，赵延明.基于SVC的电弧炉谐波抑制研究[J].中国仪器仪表，2008（1）:62-66.

[4] 赵欣.基于对称分量法的矿热炉短网补偿技术的研究[D]:[硕士学位论文].长春:长春工业大学电气与电子工程学院，2003.

[5] 任丕德，刘发友，周胜军.动态无功补偿技术的应用现状[J].电网技术，2004，28（23）:81-83.

[6] 贾文超，唐兆国.电弧炉动态运行参数的研究[J].铁合金，2010（4）:30-33.

[7] 夏祖华，沈斐，胡爱军，等.动态无功补偿技术应用综述[J].电力设备，2004，5（10）:27-31.

[8] 刘巍，谷阔，谭佳伟，等.多项式函数极小化问题的全局优化算法[J].长春工业大学学报:自然科学版，2010，31（6）:605-608.