时滞微分方程弱解的最终可微性

王惠玲， 王文彧

（山西农业大学信息学院，山西晋中 030800）

考虑如下形式的时滞微分方程:

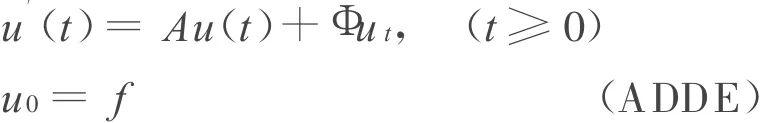
其中

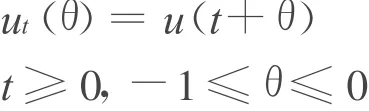
和

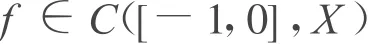
虽然（ADDE）弱解的最终可微性看起来是一个自然的问题，但在这个课题的研究上，仅发现了几篇文献[1-4]。而文献[2-4]都作用在Lp空间上，考虑了在标准X值函数空间上T（t）是解析和Φ是无界（但在某些意义下关于 A相对有界）的情况。而文献[5]是作用在C（[-1，0]，X）空间上，且较文献[2-4]而言，在 Φ上有较强的假设，即Φ有界，但在T（t）上的条件却是最优的。它利用A的预解式显得表达出了半群VΦ的生成元的预解式，再根据文献[6]的定理2.4.7得到VΦ的最终可微性，进而由 VΦ的最终可微性推出（ADDE）弱解的最终可微性。

文中继续探讨（ADDE）弱解的最终可微性问题，也就是相应于任一初始值f，（ADDE）的弱解是否在[t0，∞）对某个t0是（ADDE）的古典解。文中仍然假定Φ有界，但T（t）立刻可微和Φ的值域R（Φ）⊂D（A）中，在这些条件下，直接利用可微性的定义来讨论（ADDE）的弱解u（t）对某个t0的最终可微性。

考虑时滞微分方程（ADDE），假定A生成X上的一个C0半群{T（t）:t≥0}，Φ:C（[-1，0]，X）→X是一个有界线性算子。

为了通过半群的方法解决（ADDE），我们引入相应的C（[-1，0]，X）空间上的时滞微分算子（BΦ，D（BΦ）），定义为:

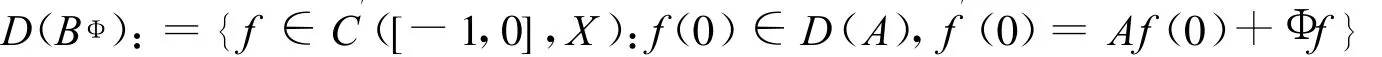
定理 1[7]定义（1）中的算子 BΦ生成C（[-1，0]，X）空间上的强连续半群{VΦ（t）:t≥0}。

半群{VΦ（t）:t≥0}有下面的平移性质:

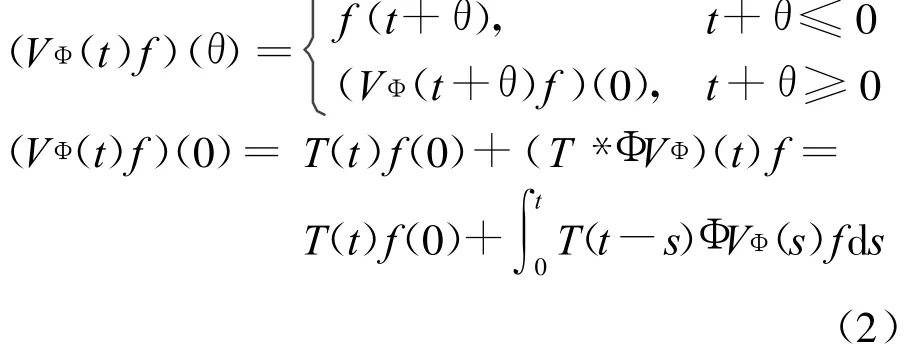
下面的命题总结了VΦ与（ADDE）弱解之间的关系，并证实了（ADDE）是适当的。

命题1[5]f∈C（[-1，0]，X），定义

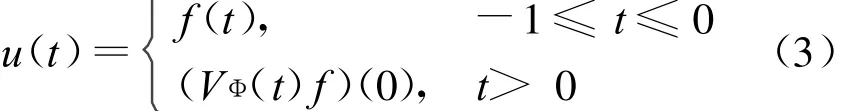
1）u是（ADDE）的唯一弱解。

2）如果 f∈D（BΦ），那么u是（ADDE）的一个古典解。

3）如果u′（t）对某个t≥0存在，那么u（t）∈D（A）且u′（t）=Au（t）+Φ ut成立。

定理2 时滞微分方程（ADDE），A生成X上的一个立刻可微半群{T（t）:t≥0}，Φ:C（[-1，0]，X）→X有界，且Φ的值域R（Φ）⊂D（A），则时滞微分方程（ADDE）的弱解最终可微。

证明:由命题知（ADDE）的弱解为:

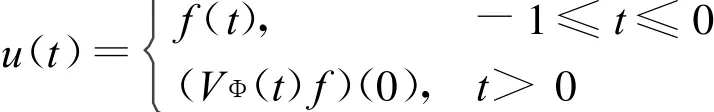
下面考虑t＞0的情况，由式（2）和式（3）有:

T（t）可微，得到

由于Φ的值域R（Φ）⊂D（A）

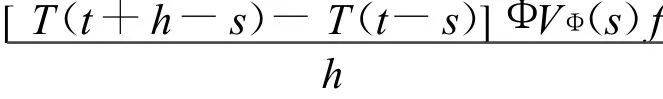
下面证明，当h→0时

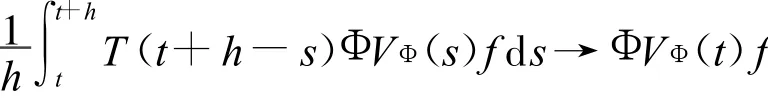
当h→0时，s→t，t+h-s→0，故当0≤h＜δ时，由T（t）的强连续性，有

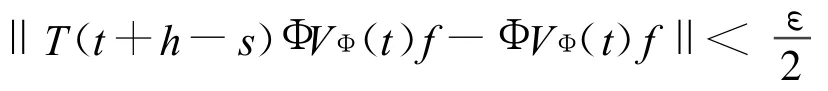
又由 Φ，VΦ的有界性有，当0≤h＜δ时

所以

故

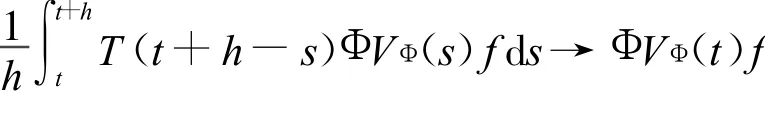
所以

因此，时滞微分方程（ADDE）的弱解最终可微。证毕。

[1] Andras Batkai，Susanna Piazzera.Semigroups for delay equations in Lp-phase spaces[M].[S.l.]: Book Manuscriptin Press，2003.

[2] G Di Blasio.Differentiability of the solution semigroup for delay differential equations[C]//G.R.Goldstein，R.Nagel，S.Romanelli（Eds.）.Evolution Equations:Dekker，2003:147-158.

[3] G Di Blasio，K Kunisch，E Sinestrari.Stability for abstract linear differential equations[J].Israel J. Math.，1985，50:231-263.

[4] E Sinestrari.A noncompact differentiable semigroup arising from an abstract delay equation[J].C. R.Math.Rep.Acad.Sci.Canada，1984，6:43-48.

[5] Charles J K Batty.Differentiability and growth bounds of solutions of delay equations[J].J. Math.Anal.Appl.，2004，299:133-146.

[6] A Pazy.Semigroups of linear operators and applications to partial differential equations[M].New York:Springer-Verlag，1983.

[7] K J Engel，R Nagel.One-parameter semigroups for linear evolution equations[M].New York:Graduate Texts in M ath.Springer-Verlag，2000.

[8] 周民强.实变函数[M].北京:北京大学出版社，2001.