次分量分析恒模盲多用户检测算法

刘顺兰，张鹏

(杭州电子科技大学通信工程学院，浙江杭州310018)

0 引言

在码分多址通信中，当通信用户数比较多时，多址干扰成为最主要的干扰。由于多用户检测可以提高系统容量，克服远近效应的影响，而成为克服多址干扰的有效技术。盲多用户检测［1－6］技术由于只需要待检测用户的观测数据，而不需要其他的用户信息而成为多用户检测的主要发展方向。这方面主要的技术有解相关多用户检测，MMSE多用户检测，恒模算法盲多用户检测，Kalman滤波器盲多用户检测，最小输出能量盲多用户检测和基于子空间盲多用户检测等。传统的恒模算法［2］收敛速度太慢，且非常容易捕获到干扰用户的信息而非期望信号。最小二乘恒模算法［5］对线性无关的输入数据能确保全局收敛性和稳定性，收敛性能有所提高。本文提出了一种基于次分量分析恒模算法［7］的盲多用户检测算法，与最小二乘恒模算法，线性约束的最小二乘算法［8］等相比在信干比和误码率方面有明显的改善。

1 信号模型

考虑一个用户数为K的二进制DS-CDMA基带通信系统，假设噪声为加性高斯白噪声，则接收的信号波形为:

式中，T为用户的码元周期;Ak为第k个用户信号到达基站时的幅度;bk为第k个用户传输的信息序列，bk(i)∈{－1，+1};sk(t)为第k个用户的归一化传输信号波形(扩频码);n(t)为实部和虚部统计独立且功率谱密度为σ2的基带高斯噪声。

当系统同步时，只需要考虑一个比特周期内的信号检测，因此不妨省略i得到:

在接收端按码片速率采样，可得到N×L的输出样本矩阵r，L是接收到的符号数:

式中，S=[s1，s2，...，sK]，A=diag(A1，A2，...，AK)，b=[b1，b2，...，bK]T。n是高斯噪声的采样矩阵，具有零均值和相关单位矩阵I。

2 次分量分析恒模算法

次分量分析［7，9］恒模算法是在恒模代价公式的基础上，满足wwH=1的约束条件，推导出一种Rayleigh熵形式的代价函数。本文将其应用于多用户检测，推导出最优权矢量对应于Rayleigh熵的极小值点［9］。

次分量分析恒模算法的代价函数［7］为:

假设式4满足约束条件，则可以推导出:

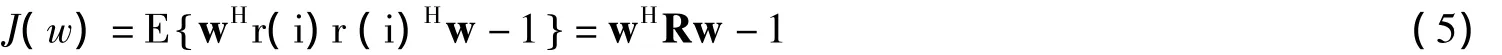
式中，R=E［r(i)r(i)H］，寻找最优权矢量wopt使代价函数最小，即:

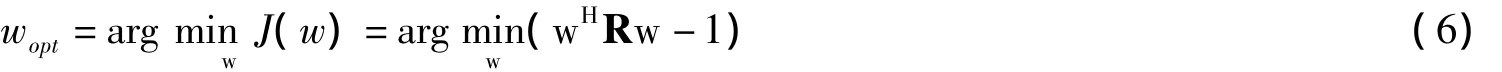
把约束条件wwH=1代入式5中，可以得到:

式中，R'=R－I，对式7变换得:

这就是Rayleigh熵的形式，由Rayleigh熵的性质，可知Rayleigh熵的极小值对应于矩阵R的最小特征值，为了找寻这些极值点，计算梯度:

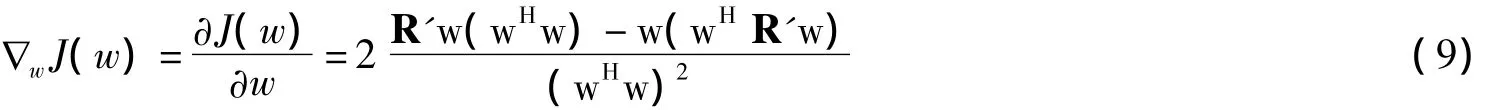
由式9可以看到对应于梯度为零的稳定点满足:

若w为对应于特征值λ=wHR'w的R'的单位长度特征矢量，则可以满足式9。可以看出，最小特征值对应的特征向量即为最优权矢量。采用文献10提出的实时迭代算法进行权值优化，可得应用于盲多用户检测中的次分量分析恒模算法的迭代公式为:

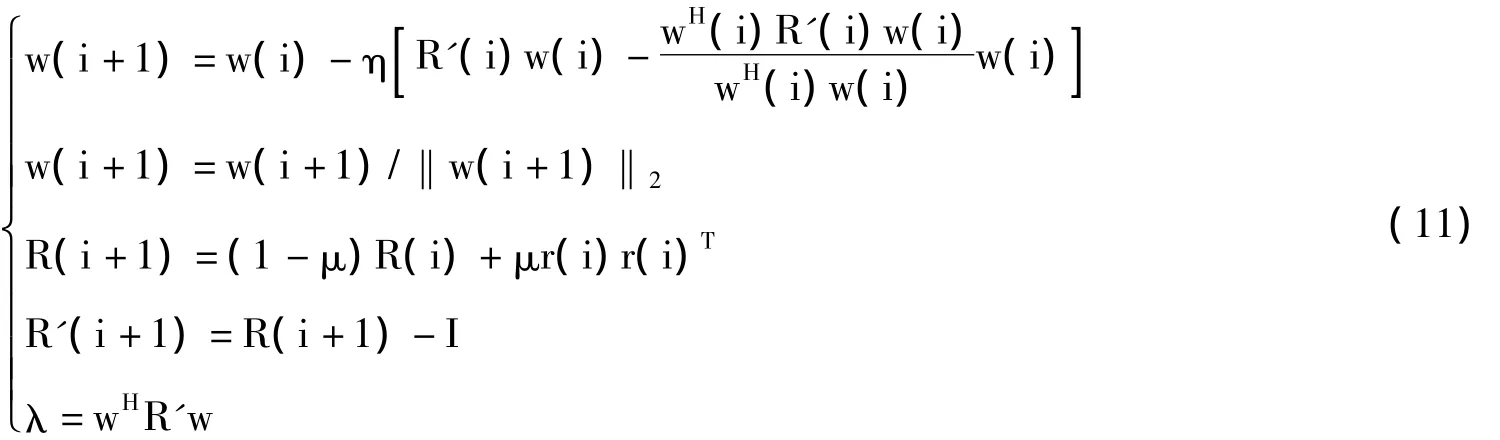
式中，η和μ分别为步长因子。

3 仿真分析

多用户检测器的主要性能指标包括:误码率、信号干扰噪声比、渐近多用户有效性和抗远近能力等。本节将通过仿真对次分量分析恒模盲多用户检测算法与传统的最小二乘恒模算法、线性约束最小二乘恒模算法进行性能对比。仿真考虑DS-CDMA系统，AWGN信道，使用N=31的GOLD序列扩频，系统用户数为6个，存在5个干扰用户，干扰用户与待检测用户功率之比为A2k/A21，k=2，3，...，6，多址干扰MAI=10lg(A/A)。用MCA-CMA、LSCMA、LCLSCMA分别表示次分量分析恒模盲多用户检测算法、最小二乘恒模算法以及线性约束最小二乘恒模算法仿真结果中用直线表示MCA-CMA、虚线表示LSCMA、点划线表示LCLSCMA。

实验1以信干比作为性能尺度。仿真在相同多址干扰MAI=10lg(A2k/A21)=10dB k=2，...，6，SNR=10的条件下进行的。输出信干噪比随迭代次数的变化曲线如图1所示，图1中，本文提出的次分量分析恒模算法算法输出信干噪比要优于最小二乘恒模算法、线性约束最小二乘恒模算法，具有更强的抗多址干扰的能力。在迭代次数为1 000时3种算法的处理时间分别为1.645s、1.836s、2.472s。输出信干比定义为:

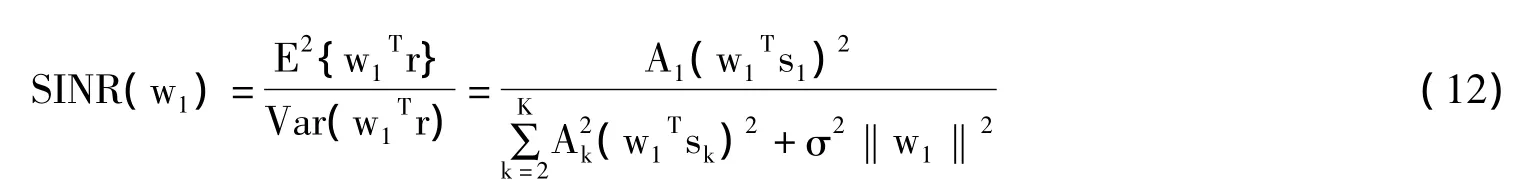
实验2以误码率作为性能尺度。仿真模拟系统远近效应MAI=10dB k=2，3，...，5。MAI=20dB，k=6。误码率随信噪比的变化曲线如图2所示，图2中MCA-CMA算法在各个信噪比的情况下误码性能都要好于最小二乘恒模算法和线性约束最小二乘恒模算法。说明本文的算法输出误码率低，检测性能较好。

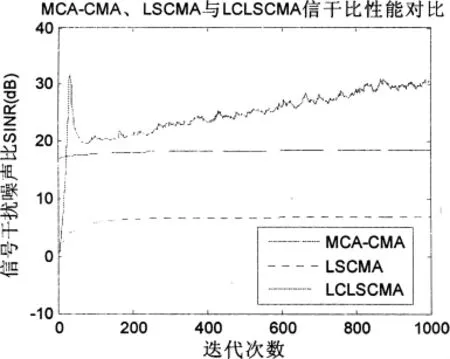
图1 SNR=10时3种方法的输出信干比

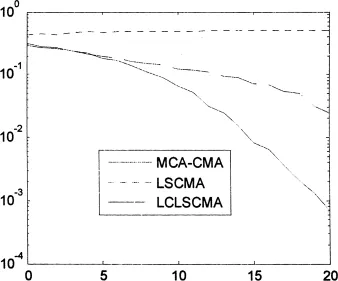
图2 3种方法的误码性能比较

4 结束语

本文在恒模多用户检测算法的基础上，提出了一种基于次分量分析恒模多用户检测算法，它利用Rayleigh熵的性质，推导出最优权矢量对应于Rayleigh熵的极小值点。仿真结果表明，新提出的算法在输出信干噪比和误码率性能上比传统的最小二乘恒模算法、线性约束最小二乘恒模算法都有很大的改善。而且由于避免了矩阵求逆的运算，大大减小了算法的复杂度。

［1］De Lamare R C，Sampaio-Neto R.Low-complexity variable step-size mechanisms for stochastic gradient algorithms in minimum variance CDMA receivers［J］.Signal Processing，2006，54(6):2 302－2 317.

［2］Treichler J R，Agee B G.A new approach to multipath correction of constant modulus signals［J］.Acoustics Speech Signal Processing，1983，31(2):459－472.

［3］Shynk J J，Gooch R P.Performance analysis of the multistage CMA adaptive beamformer［A］.IEEE Milcom Proceedings［C］.New York，1994:316－320.

［4］Agee B.The least squareS C～IA-a new technique for rapid correction ofconstant signals［C］.Los Angeles，Signal Processing，1986:953－956

［5］Wang X，Poor H V.Blind multiuser detection:A subspace approach［J］.Information Theory，1998，44(2):677－690.

［6］王淑艳，吴仁彪，石庆研.MCA-CMA次分量分析恒模算法［J］.数据采集与处理，2008，23(3):270－272.

［7］傅洪亮，酆广增.线性受限最小二乘恒模盲多用户检测算法［J］.信号处理，2005，21(5):490－493.

［8］黄磊，吴顺君.最小Rayleigh熵恒模信号分离算法［J］.电子与信息学报，2005;27(10):1 531－1 534.

［9］Andrzej cichocki，Shun—ichi amari.吴正国，唐劲松，章林柯，译.自适应盲信号与图像处理［M］.北京:电子工业出版社，2005:126－128.