基于MVEKF的被动声网络定位算法

郭云飞，苏刚，林岳松

(杭州电子科技大学信息与控制研究所，浙江杭州310018)

0 引言

随着电子干扰和反辐射导弹等雷达对抗软硬杀伤技术的发展，人们开始努力开发具有低截获特性的无源探测定位技术［1，2］。利用声传感器被动接收低空飞行器产生的特定声波可以对目标进行定位。使用多个声传感器组网，可扩大目标的探测范围，融合网内多个声传感器的方位角信息实现对网内目标的较为准确的定位和态势估计。对于解决声被动定位问题，多年来，研究者发表了大量相关论文，提出多种方法。其中一种提出测向交叉定位的方法，利用几何学原理实现目标的定位［3］;一种提出时差定位的方法，通过处理3个或多个测量站采集到的信号到达时间的测量数据对辐射源进行定位［4］;一种提出基于概率的定位方法，用服从正态分布的概率密度函数来描述传感器的一个测量，以便进一步求解目标状态［5］。本文针对声传感器在测量目标时接收到的声波信号存在量测纯方位的问题，提出一种被动声传感器网络的MVEKF定位［6，7］处理算法。首先通过给定的时延处理方法对时延信号进行处理，同时修正滤波过程中的协方差矩阵，防止其产生病态，弥补EKF算法在跟踪目标时的不足，达到稳定跟踪的目地。仿真结果说明了该算法的有效性。

1 问题和算法描述

1.1 数学模型

假设目标在二维平面内做近似匀速直线运动，则它的离散系统的目标运动状态方程及声传感器的观测方程为:

式中，X(k)=［x(k)，vx(k)，y(k)，vy(k)］T为第k时刻的状态变矩阵，(x(k)，y(k))为目标在第k时刻的位置坐标，(Sx(k)，Sy(k))为声传感器的位置，β(k)为观测值，w(k)和v(k)分别为相互独立的过程噪声和量测噪声，均为零均值高斯白噪声。

1.2 信号时延及处理

假设用两个声传感器对目标进行定位，那么，在同一融合周期内，两个声传感器上报的目标方位角量测信息不对应于目标同一位置，因此需要对方位角信息进行时延校准处理，使得在同一融合周期内，声传感器所得方位角信息对应于目标的同一位置。

假定以3个声传感器S1、S2、S3组成一个被动声传感器网络。首先根据滤波定位可以得到在时延条件下的目标初步位置为(xp，yp)，然后计算此点到各个声传感器的距离分别为D1、D2、D3。设距离关系为D1＜D2＜D3，在第k时刻各个声传感器上报的方位角信息分别为β1(kT)、β2(kT)、β3(kT)，工作时刻分别为T1(k)、T2(k)、T3(k)，以其中某个声传感器的时刻(假设为T3(k))为基准，对声传感器S1和S2上报方位角的时刻进行追溯，即:

式中，c为声速，T1(i)、T2(i)为声传感器S1和S2在T3(k)之前的某个工作时刻。当首次出现i，T1(i)、T2(i)、T3(k)3个时刻所对应的方位角信息α1(iT)、α2(iT)、β3(kT)即对应于目标的同一位置。此时，声传感器S1、S2对应的新的方位角为:

式中利用经时延处理后得到的新的方位角信息就可以重新获得目标的位置，其坐标为(x，y)。

1.3 修正协方差扩展卡尔曼滤波

传统的非线性滤波常采用扩展卡尔曼滤波方法，但这种滤波方法有很多不足之处，如具有依赖初始状态估计并受测量噪声影响大等特点，估计过程中协方差易出现病态，收敛速度慢，滤波效果不稳定。

对于高斯白噪声条件下的线性系统卡尔曼滤波，由正交定理得:

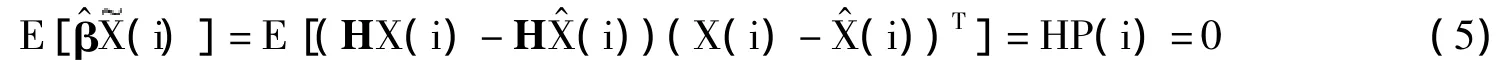
但是在实际的EKF滤波器中，由于测量方程是非线性的，且预测值(i/i－1)存在一定的偏差，导致在预测点(i/i－1)处所求得的Jacobian矩阵也存在一定的偏差，使得:

式中，P(i/i)－为EKF中第i个测量时刻滤波状态协方差阵。

针对式1所示系统，本文提出的MVEKF方法的基本思想是在计算出状态滤波值(i/i)之后，重新计算Jacobian矩阵:

利用新的Jacobian矩阵作为测量矩阵对协方差矩阵进行更新，得到更加准确的修正协方差矩阵P(i/i)+，使得:

用滤波值计算的H(i)+进行卡尔曼滤波增益和滤波协方差阵的计算，由于其中隐含了当前时刻的测量值的信息，因此能够改善非线性估计的性能。

2 仿真及性能分析

设定如下场景:目标做匀速直线运动，初始状态为x0=5 000m，vx=45m/s，y0=4 000m，vy=－45m/s。用3个声传感器S1(7 991m，1 879m)，S2(4 670m，1 319m)，S3(6 576m，4 569m)组成一个被动声传感器网络。场景如图1所示。参数:声传感器独立工作，工作周期为1s，测量误差为3°。分别用EKF方法和本文算法对目标状态进行更新，经过时延处理后两种定位算法对目标的定位距离误差比较曲线如图2所示。从定位效果来看，采用本文算法的定位轨迹平均误差为30.8m，而EKF算法的定位轨迹的平均误差为50.2m。可见，本文算法完全适用于带有时延的纯方位量测目标定位问题，且定位精度高。

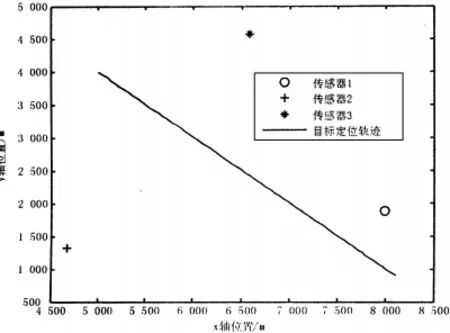
图1 目标运动场景

图2 误差比较

3 结束语

本文分析了非线性的无源定位模型，针对声传感器测量目标发出的声波信号存在测量纯方位的特点，提出一种被动声传感器网络的MVEKF定位算法。由仿真结果可以看出，本文算法与EKF算法相比，定位精度更高，收敛速度更快。验证了该算法具有更好的跟踪性能。

［1］Chen Ling，Shaohong Li.IMM Tracking of a 3D Maneuvering Target with Passive TDOA System［A］.Nan Jing，China:International Conference on Neural Networks and Signal Processing［C］.2003:14－17.

［2］Lo K W，Ferguson B G.Broadband passive acoustic technique for target motion parameter estimation［J］.Aerospace and Electronic Systems，2000，36(1):163－175.

［3］孙仲康，陈辉煌.定位导航与制导［M］.北京:国防工业出版社，1987:125－160.

［4］戴剑华，尹成友，黄冶.三星时差定位系统的数据关联与定位算法［J］.现代雷达，2002，(2):21－38.

［5］胡来招.无源定位.北京:国防工业出版［M］，2004:41－60.

［6］孙仲康，郭福成，冯道旺，等.单站无源定位跟踪技术［M］.北京:国防工业出版社，2008:320－350.

［7］郭福成，李宗华，孙仲康.无源定位跟踪中修正协方差扩展卡尔曼滤波算法［J］.电子与信息学报，2004，26(6):917－922.