中子多重性移位寄存器功能模拟实现
管才路 张全虎 王中杰 刘 杰
(第二炮兵工程学院 西安 710025)
中子多重性测量是军控核查研究中的重要属性测量技术,在军控核查和核安全保障领域中应用广泛[1]。不同于传统的符合测量方法,多重性测量分别记录中子符合分辨时间内的分布情况,得到二重符合中子、三重符合中子、四重符合中子等更多重符合中子,所以中子多重性测量在处理中子脉冲时采用更为先进的多重性移位寄存器来处理中子脉冲[2]。本文在研究多重性移位寄存器(Multiplicity Shift Register, MSR)工作原理基础上,用C语言编程模拟MSR,以处理中子脉冲序列,为后续计算得到样品信息奠定基础。
1 MSR原理
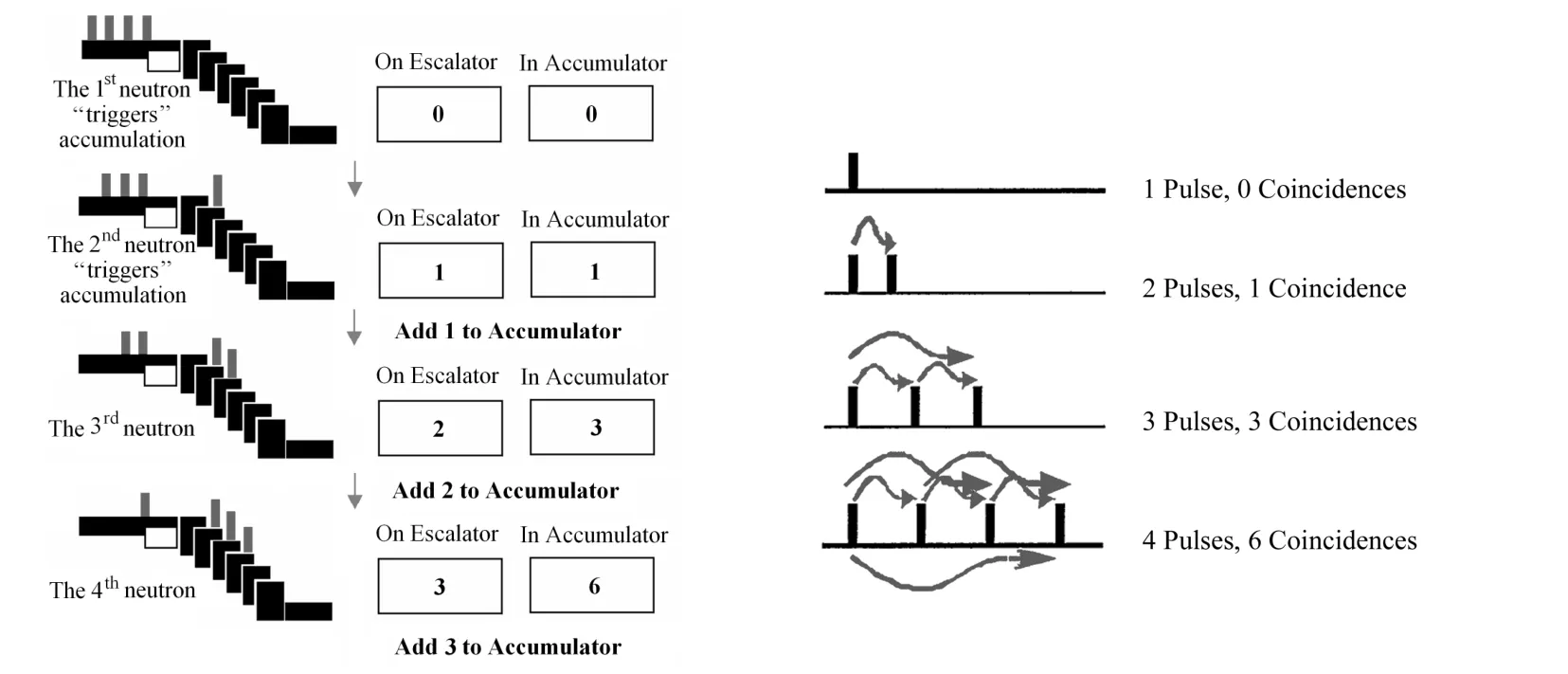
图1 移位寄存器处理四个脉冲以及这四个脉冲的可能符合情况Fig.1 Example of shift register operation with four neutron pulses and possible coincidence pairs between 1, 2, 3 or4 pulses.
自发裂变、诱发裂变可同时发射1个或多个中子,脉冲序列既可看作是事件随时间的分布,也可以看作是裂变事件间的时间间隔分布。理想的中子脉冲序列有相关事件和非相关事件,相关事件与非相关事件的时间间隔较大,没有干扰。实际的脉冲序列则要复杂很多,主要是因为不同的本底事件之间、不同的裂变事件之间、本底事件与裂变事件之间的交迭。样品发射出的中子在经过一系列的慢化、散射之后,被探测、吸收或逃逸。在此过程中,中子的数量逐渐减少,其规律遵循Rossi-a分布[3]。移位寄存器能在实际测量中处理中子脉冲序列输出真符合和偶然符合计数。
1.1 传统移位寄存器
符合电路在计数时,会受到门宽G的影响,即损失门宽时间内的符合计数。传统移位寄存器可很好解决此问题[3]。与符合电路不同,移位寄存器保存每个通过移位寄存器的脉冲,而这些脉冲都会产生自己的符合门与其他的脉冲比较,其算法可用图1来说明。
当4个相关联的中子脉冲通过移位寄存器时,移位寄存器的可逆计数器(Up-down Counter)类似于电梯,电梯上同时出现的中子数量可有0、1、2、3四种情况,累加器计数分别是0、1、3、6,最后共有6种符合情况。也即对n个事件,记录到的符合计数为n(n–1)/2,即组合数Cn2。移位寄存器原理示意图如图2所示:
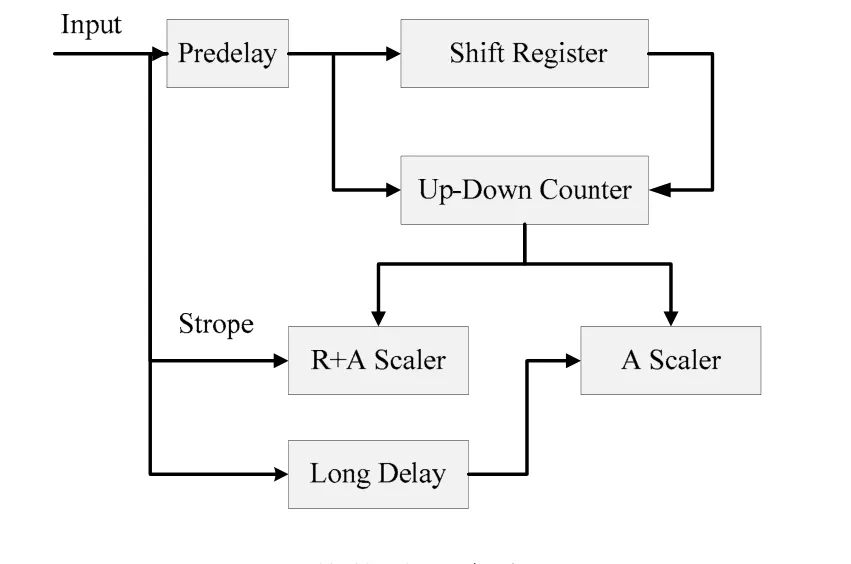
图2 传统移位寄存器Fig.2 Conventional shift register circuit.
输入脉冲首先触发 R+A计数器,将可逆计数器[4]中的脉冲数记录到R+A计数器中,选通脉冲经过一个较长延迟(~4096 μs)后,再将可逆计数器中脉冲数存入A计数器中;然后输入脉冲进入预延迟电路,经过预延迟后进入移位寄存器。
1.2 多重性移位寄存器
图3是MSR的工作示意图。MSR的基本原理与传统移位寄存器类似,不同之处在于它可以记录符合时间内脉冲个数的分布[4]。 基于这一思想,使中子脉冲序列的每一个中子脉冲都激发一个门宽,判断后面的中子脉冲信号有多少在该门宽内,并记录下来。如有1个在该门宽内,则标记为“1”的计数器加1,若有2个在该门宽之内,则标记为“2”的计数器加 1,依次进行判断。这样记录下来的中子脉冲既含有真符合事件,也含有偶然符合事件。为得到偶然符合事件的计数分布,可随机激发产生与上述门宽相同数量的同宽度门宽,判断后面的脉冲信号是否在此门宽内,采用同样的记录方式,这样得到的就是偶然符合计数。偶然符合计数也可通过脉冲长延迟后激发一个同宽度门宽来得出,处理方式相同。

图3 MSR工作示意图Fig.3 Multiplicity shift register circuit.
2 MSR参数
MSR 的参数主要有符合门宽(tg)、死时间(δ)、预延迟(tp)、长延迟(t))。在模拟时,也要根据实际情况设定合适的参数。
(1) 符合门宽:MSR在一个中子脉冲到达时,激发产生有一定宽度的时间,比较此脉冲后所有脉冲到达的时刻是否在此宽度内。门宽若过小,则有可能漏记真符合事件,过大,则大量偶然符合事件也被记录,两种情况都造成真符合事件计数(R+A)-A和偶然符合事件计数A的误差偏大。
(2) 死时间:由于受探测器电流收集时间、脉冲成形时间、基线恢复时间、脉冲甄别或门(OR gate)电路、移位寄存器同步输入等影响,测量中会有死时间,造成中子计数率损失与测量误差[5]。
(3) 预延迟:由于电子器件的影响,一个中子脉冲到达时,并不能立即激发产生一个门宽,所以增设预延迟电路,预延迟tp值已固化在MSR电路中[6]。但在模拟MSR时,不存在电子器件的影响,可以根据需要设定一个预延迟,也可不考虑预延迟,即:tp=0。
(4) 长延迟:其目的是测量偶然符合事件计数,长延迟之后激发的门宽内中子脉冲相对于激发脉冲信号都是偶然符合事件。长延迟的值要适当选择,如过小,则长延迟后的门宽内有可能含真符合事件,测量结果不准确。
3 MSR模拟及结果
基于上述原理和思想,本文利用计算机C语言编写程序,通过 MATLAB软件运行后,实现了对MSR功能的模拟,并用该程序对模拟钚样品中子脉冲序列进行了分析。图4为模拟示意图。

图4 MSR模拟示意图Fig.4 Sketch map of MSR computer simulation.
4π立体角计数器模拟测量238Pu样品输出的中子脉冲序列为:2.7831200E–7、7.2670700E–7、7.7297311E–5、 1.1569005E–4、 1.1734291E–4、8.8941688E–4、 8.9037518E–4、 8.9320438E–4、1.0966829E–3、 1.9703140E–3、 1.0966829E–3、1.9739338E–3、 2.4581264E–3、 2.6776674E–3、2.6781093E–3、2.67810939E–3、2.7074169E–3、2.7139145E–3、3.4010066E–3、3.4045689E–3, ··。
用该MSR程序分析上述脉冲序列,得到(R+A)和(A)的分布情况,见表1,bin为计数的标记分类。
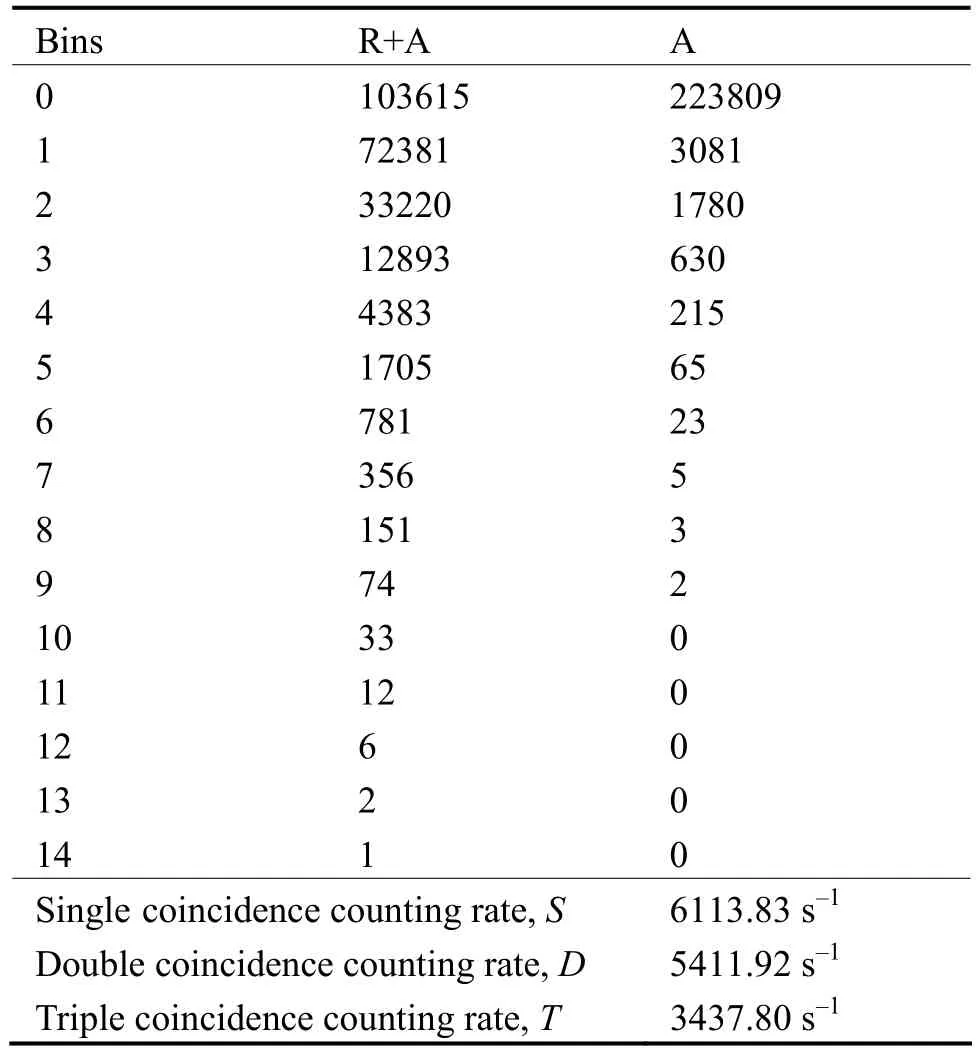
表1 238Pu模拟测量数据的中子多重性情况Table1 1Neutron multiplicity distribution from simulation data of 238Pu
4 分析与结论
由表1,在bin=0时,A的数据甚大于A的其它数据,多重性次数多达223809次,偶然符合计数非常少。其原因主要有两点:(1)本次所用的计数器是一种理想的模型,其衰退时间非常短,只要裂变产生中子,就立刻被3He俘获;这就使偶然符合计数减少;(2)对于计算机模拟而言,所产生的中子脉冲序列以及MSR的处理相对于实际测量时较理想,不存在实际测量中的电子学器件的影响,使偶然符合计数减少。
在得到(R+A)和A的分布后,计算它们的阶乘矩,得到中子多重性测量方程的一重符合计数率(S)、二重符合计数率(D)、三重符合计数率(T),求解测量方程可得到样品信息。计算结果与相同条件下的实验数据偏差较小[7],说明本文所采用的模拟方法是正确可行的。
1 Ensslin N, Harker W C, Krick M S, et al.Application guide to neutron multiplicity counting [Z].USA: Los Alamos National Laboratory, 1998, 5–10
2 丁大钊, 叶春堂, 赵志祥, 等.中子物理学 [M].北京:原子能出版社, 2001, 100–102 DING Dazhao, YE Chuntang, ZHAO Zhixiang, et al.Neutron physics [M].Beijing: Atomic Energy Press, 2001,100–102
3 许小明.中子多重性测量技术研究 [D].北京: 中国原子能科学研究院, 2008, 32–34 XU Xiaoming, Development of neutron multiplicity counting [D].Beijing: China Institute of Atomic Energy.2008, 32–34.
4 Ensslin N, Krick M S, Langner D G.Passive neutron multiplicity counting [Z].USA: Los Alamos National Laboratory, 1991.13–15
5 Dytlewski N.Dead time corrections for multiplicity counters [J].Nucl Instr Meth, 1991, A305:492–494
6 Krick M S, Swansen J E.Neutron multiplicity and multiplication measurements [J].Nucl Instr Meth, 1984,A219: 384–393
7 Peerani P, Weber A, Swinhoe M T, et al.ESARDA multiplicity benchmark exercise [J].Esarda Bulletin, 2009,42: 1–15

