基于GPU并行计算实现快速显微CT重构

沈 飞 陈荣昌 肖体乔

1 (中国科学院上海应用物理研究所 上海 201800)

2 (中国科学院研究生院 北京 100049)

近些年来，三维CT在医学和工业领域得到广泛应用。随着探测器分辨率的改进，CT投影图像采样分辨率也不断提高，对高质量输出容积体期望值的不断提升，使存储容量和数据的处理量越来越大，严重影响CT重建速度。目前，上海光源成像线站采用串行的 CT重建程序并通过 CPU完成计算，计算数据容积为2 048×2 048×1 500，就需40多小时，迫切需要进行CT重建的加速。

图像处理器(GPU, graphics processing unit)是高度并行化的流式处理器，并行计算能力强，运算速度快，在通用计算(GPGPU)领域有极大优势。文献[1]利用 GPU 实现 FDK 算法(The algorithm of Feldkamp, Davis and Kress)的加速，最高可达15倍左右的加速比。Scherl[2]利用 CUDA在 NVDIA Geforce8800实现了FDK算法，取得5倍左右的加速比。

使用FDK算法和迭代算法进行CT重建的GPU加速研究，已取得较佳效果[3−5]。而基于滤波反投影算法的GPU加速的研究并不多见，该法的主要优点是重建速度快。本文采用滤波反投影(FBP)算法实现CT重建，由于反投影时每个位置的像素值重建相互独立，可同时进行重建计算，故可将其并行化设计。

1 GPU并行化实现CT重建

1.1 CUDA编程模型

CUDA编程模型[6]将CPU作为主机(Host)，GPU作为协处理器(co-processor)或设备(Device)。一个系统中可存在一个主机和若干个设备，采用单指令、多线程执行模式(SIMT)。

模型中CPU和GPU协同工作，各司其职。CPU负责进行逻辑性强的事务处理和串行计算，GPU则专注于执行高度线程化的并行处理任务。CPU和GPU各自拥有相互独立的存储器地址空间：主机端的内存和设备端的显存。

一旦确定了程序中的并行部分，即可考虑把这部分计算工作交给GPU。将运行在GPU上的并行计算函数称为kernel(内核函数)。一个kernel函数并不是一个完整的程序，而是整个CUDA程序中一个可被并行执行的步骤(图1)。一个完整的CUDA程序，是由一系列设备端kernel函数并行步骤和主机端串行处理步骤共同组成。这些处理步骤会按照程序中的相应语句顺序依次执行，满足顺序一致性。

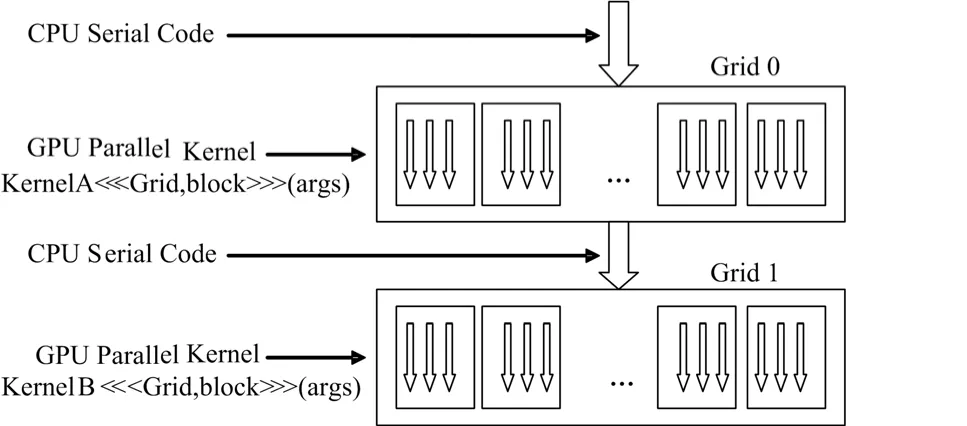
图1 CUDA编程模型Fig.1 Programming model of CUDA.

进行GPU代码设计时，对全局现存的访问是否符合合并访问条件是对 CUDA程序性能影响最明显的因素之一，可能产生一个量级的差距。因为，若符合一定的访问条件，只需一次传输即可完成一个Half-warp所有线程的数据访问[6]。

1.2 CT重建kernel的设计

滤波反投影重建是一种解析方法，先获取某一层所有角度的投影数据得到正弦图，再进行滤波降噪处理，最后进行反投影重建得到断层每个位置的像素值，其优点是重建速度快[7]。

1.2.1 正弦图

滤波反投影前，需获取重建切片的正弦图，由于直接获取的正弦图含有背景噪声，需去除之，我们采用的方法如式(1)：

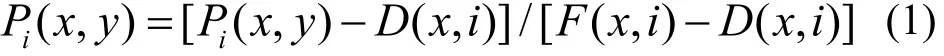
式中，Pi(x,y)为第 i层切片(x,y)处的像素值，D(x,i)为无光照时第 i层切片(x,i)处的像素值，F(x,i)为有光照无样品时第i层切片(x,i)处的像素值。

由式(1)，每个坐标处的计算互不相干，可并行执行，则可在CPU代码中获取正弦图数据，并编写kernel函数去除背景噪声，可见kernel执行过程的数据访问符合合并访问的条件。

1.2.2 滤波处理

由于滤波反投影算法会带来星状伪迹，故需进行滤波消除伪迹。本文采用Sheep Logan滤波函数进行滤波处理，用滤波函数重建图像，其振荡响应减小，对于含有噪声的投影数据，重建效果较好[8]，其函数式为：

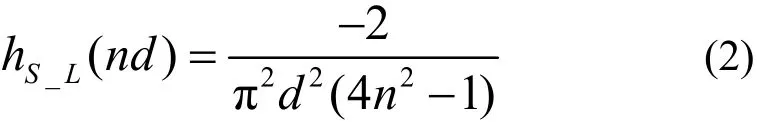
式中，n为取值范围(−width/2,width/2)，width为图像的宽度；d取1。其图形如图2所示。

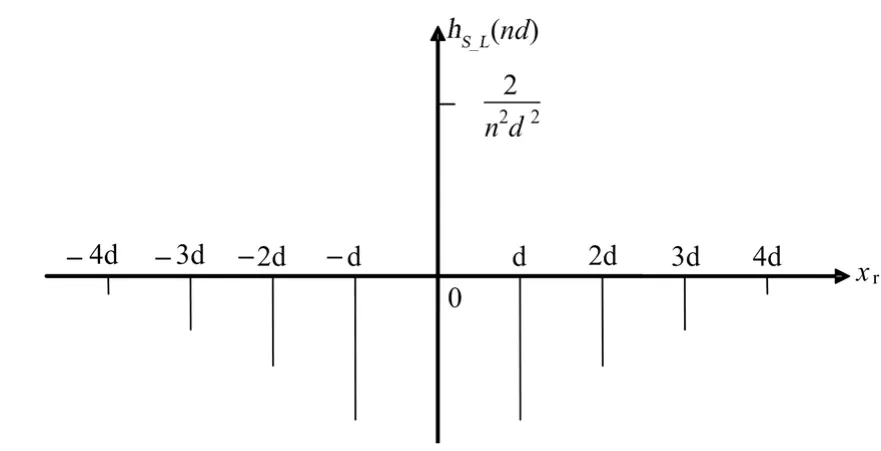
图2 S_L滤波函数的离散表示Fig.2 Discrete representation of S_L filter function.

将图像函数和滤波函数进行卷积操作，即：

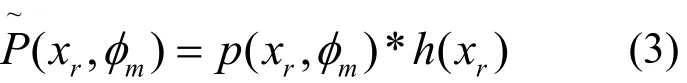
由于CUDA有FFT和IFFT的API，本文采用傅里叶变换方式求卷积，滤波函数的取值范围和图像的宽度相一致。傅里叶变换后求乘积即位置相对应的点相乘，可将其并行化处理，而且两个函数的宽度一样，所以kernel在执行时其数据访问符合合并访问的条件。

1.2.3 反投影

CT重建的计算量主要在反投影部分，反投影部分的加速效果直接影响重建过程的加速比。反投影过程即为累加求和的过程，在进行累加求和前需进行射束计算和线性内插。图像重建时指定切片的像素为N×N，如图(3)所示。

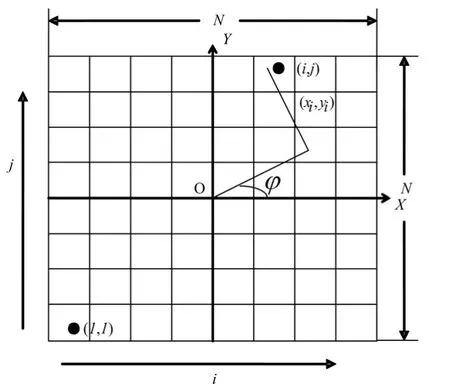
图3 图像重建时所用的坐标系Fig.3 Coordinate system of image reconstruction.

滤波反投影公式为：

由式 4，图像重建时每个点的重建互不干扰，且每个点重建的方法相同，只是重建时所需的数据不一样。所以，单个切片的每个坐标处的重建是可以并行执行的。

由于重建时数据的访问不符合合并访问的条件，带有随机性，所以采用将数据映射到纹理存储器。纹理存储器通过缓存利用数据的局部性提高效率，使用纹理时未严格遵守合并访问条件，也能获得较高的带宽[6,8]。

2 实验结果与分析

实验平台的配置为：中央处理器Intel i5-650，图形处理器NVIDIA GTX295，内存Kingston DDR3 4GB，操作系统Windows XP Professional SP2 X86，显卡驱动NV driver 190.20 + CUDA 2.3 SDK。

开发工具为 Visual Studio2005，主机端使用C++进行编程，设备端采用CUDA标准的类C语言进行编程。

我们在CPU中进行CT重建时，采用单精度浮点型数据进行保存，而GPU支持双精度浮点运算，其重建结果符合实验要求(图4)。

图4 CPU和GPU重建结果的比较Fig.4 Comparison of reconstruction between CPU and GPU.

由于GTX295拥有30个流多处理器(SM)，而每个SM中拥有8个SIMD的流处理器(SP)，总计算核心达 240个。实验中对尺寸为 704×301×1 200的数据进行了重建的加速(704和301是图像的高度与宽度，1 200是投影数)，其中对单张切片的正弦图处理、滤波、反投影部分采用GPU加速后的时间进行了比较，结果见表1。

由表1，除去数据传输的延时，使用GPU加速，其正弦图处理和滤波部分可得到200倍以上的加速比，而在反投影部分，将数据映射到纹理存储器中，其加速比增加一个量级。本实验还对尺寸为1 016× 1 016×1 620和2 048×2 048×1 500的物体进行重建加速的比较，计算部分的加速比都在150倍以上。

表1 某一层数据重建的时间(物体尺寸：704×301, 投影数：1 200)Table 1 Reconstruction time of a slice(object size, 704×301; projection number, 1 200).

随着数据量的不断增加，CPU读取硬盘数据及CPU内存与GPU显存之间数据传输的时间不断增加。对不同容积的数据，读取硬盘数据和 CPU与 GPU间数据传输并将数据写存到硬盘的总时间见图5(a)；图像重建的加速比见图5(b)。

由图5(b)，当重建的数据大小达到一定程度时，其整体的加速比会降低，这是因为当数据量增至一定程度，其计算部分的加速比达到饱和，而此时CPU的内存和GPU的显存之间以及CPU内存和硬盘之间数据传输的时间随着数据尺寸而增大，从而使整体的加速比降低。

图5 不同容积的数据传输时间(a)和加速比(b)的比较Fig.5 Comparison of different data sizes in transmission time (a) and speedup ratio (b).

3 结语

本文研究了通过 GPU加速使用滤波反投影原理的CT重建方法，得到了比较理想的结果。实验表明，支持单精度的GPU重建图像质量完全符合要求，其单张切片的重建可得到150多倍的加速比。GPU强大的计算能力可用于快速CT重构，是一种性价比较高的重构算法。若采用多GPU进行CT重建的加速，则加速比更高，甚至直接用于实时 CT重构。

1 FANG Xu. Real-time 3D computed tomographic reconstruction using commodity graphics hardware[J]. Phys Med Biol, 2007, 52(12): 3405–3419

2 Scherl H. Fast GPU-based CT reconstruction using the Common Unified Device Architecture (CUDA)[Z]. IEEE Nucl Sci Symp, Med Imaging Conf, 2007, (6): 4464–4466

3 Mueller K, Yagel R. Rapid 3-D cone-beam reconstruction with the Simultaneous Algebrmc Reconstruction Technique(SART) using 2-D texture mapping hardware[J]. IEEE Trans Med Imag, 2000, 19(12): 1227–1237

4 Sharp G C. GPU-based streaming architectures for fast cone-beam CT image reconstruction and demons deformable registration[J]. Phys Med Biol, 2007, 52(19): 5771–5783

5 胡君杰. 利用 GPU实现三维图像重建方法研究[J]. 世界科技研究与发展，2008, 30(1): 24–26

HU Junjie. The research of 3-D image reconstruction in GPU[J]. Res Dev world, 2008, 30(1): 24–26

6 张 舒. GPU高性能运算之CUDA[M]. 北京: 中国水利水电出版社，2009: 16–168

ZHANG Shu. High performance computing of GPU–CUDA[M]. Beijing: China Water Power Press, 2009: 16–168

7 庄天戈. CT原理与算法[M]. 上海: 上海交通大学出版社，1992: 30–60

ZHANG Tiange. The principle and algorithm of CT[M]. Shanghai: Shanghai Jiaotong University Press, 1992: 30–60

8 马车平. GPU多重纹理加速三维ct图像重建[J]. 计算机工程与应用，2008, 44(7): 227–230

MA Cheping. Accelerating the 3-D CT image reconstruction with multiple texture of GPU[J]. Comput Eng Appl, 2008, 44(7): 227–230