基于TDOA定位GSM移动台的信号处理算法

王红军

(解放军电子工程学院,合肥 230037)

1 引 言

无线定位技术是实现无线定位业务的技术基础,是指通过对接收到的无线电波的一些参数进行测量,根据特定的算法以判断出被测物体的位置,测量参数一般包括传输时间、幅度、相位和到达角等,定位精度取决于测量的方法。GSM移动通信在全球范围内应用广泛,有很多成功的商用系统,因此在GSM数字移动通信系统(以下简称GSM系统)中应用无线定位技术有很大的意义和价值。

目前,在GSM系统中采用的定位方式基本分为3类:基于电波场强的定位法、基于电波到达入射角(AOA)的定位法和基于电波到达时间(TOA)或到达时间差(TDOA)的定位法。相比之下,当前最为主流、研究最多、定位精度较高的定位算法为基于TOA的定位算法和基于TDOA的定位算法。笔者在项目研究中结合实际需求,工程中实现了基于TDOA算法定位GSM移动台的技术。本文的技术突破源于算法在工程实现时,摆脱了通常测定TDOA需依靠基站和移动台的协同来完成的局限,而利用研制成功的基于GSM系统的MLSE接收机来独立完成,极大地提高了定位GSM移动台的灵活性且无需对基站和移动台进行任何改造。

2 TDOA定位算法的信号处理模型

获得TDOA有两种方式:一是求两个接收机的信号到达时间(TOA)之差值来获得TDOA;另一种是采用相关技术,将一个接收机接收的信号与另一个接收机接收的信号进行互相关运算以获得TDOA。设计时采用了第一种方式,定位时,参与定位每个接收机都接收移动台的传输信号,记录信号的到达时间,并把TOA发送给定位中心,由定位中心完成时延的测定。下面以3个接收机为例来说明定位算法的信号处理模型。

设被定位移动台在平面上的坐标为(x,y),接收机1的坐标为(x1,y1),接收机2的坐标为(x2,y2),接收机3的坐标为(x3,y3),接收机的位置坐标由自配的GPS来确定。被定位移动台到1、2号接收机的TOA差值为 T1,到1、3号接收机的TOA差值为T2,T1、T2分别乘以光速 c得到距离差为a1和a2,则移动台轨迹可由如下方程来表示:

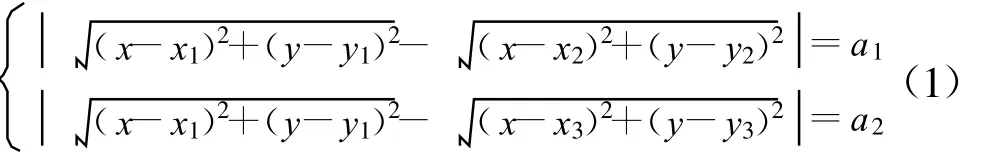
经过化简可以证明这个方程组的每一个方程均表示了一条双曲线,所以同一个移动台的信号到达两个接收机的时间差就决定了一条移动台所在的双曲线轨迹。测出两条双曲线轨迹相交点的值就可以得出移动台的位置,如图1所示。在某些环境下,可能出现两条双曲线轨迹相交两点,引起不确定因素,在这种情况下,可以采用TDOA多次多点测量或依靠一些相关的先验信息来解决这种不确定因素。

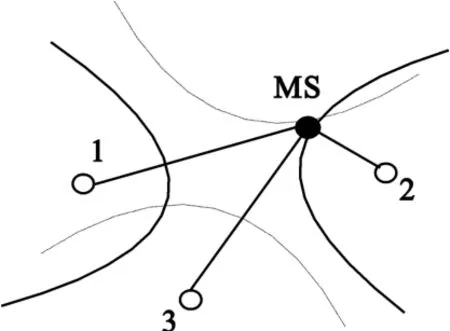
图1 双曲线定位算法的处理模型Fig.1 The processing model of the hyperbola location algorithm

利用TOA获得TDOA的方法,需要接收机与移动台之间同步且接收机之间时钟统一,否则TOA测量将产生双曲线轨迹的偏离误差。实际中接收机与移动台之间的同步由MLSE接收机在对移动台上行信号的均衡解调时实现,接收机之间的时钟问题则通过接收机配置GPS接收机和站间通信设备来解决。

3 定位算法中的信号处理技术

技术实现的前提:完成对GSM系统中被定位移动台视距传播(LOS)的RF信号的接收、A/D转换、数字化滤波和均衡解调,确定出被定位移动台信号的接收时间窗。

实现定位的设计思想是:利用GSM协议所规定的突发脉冲中8种训练序列自相关函数的特殊形状来确定接收时间窗,估计突发脉冲到达的起始时刻进而利用最大似然估计(ML)判断其到达时间,再利用TDOA算法进行定位。

按照GSM协议,8个训练序列实际上是从8个不同的周期为16的伪随机序列中截取下来的,这8个伪随机序列具有良好的自相关及互相关联特性,每个序列的中间16 bit正好是一个周期,它们是训练序列中用作相关运算的关键部分,考虑到信道冲激响应的时延扩散和接收突发的计时抖动,左右各加5 bit作为保护比特,这样训练序列比特数共为26 bit。

设计中采用了ML技术估计信号的到达时间。在进行ML估计之前,首先运用相关法进行到达时间的粗略估计,在此基础上再进行ML估计。

为解决对GSM移动台进行有效定位的问题,设计了专用的定位接收机,其原理图如图2所示,图中虚线部分采用DSP信号处理技术完成,图示的相关运算实际是均衡同步的过程。由于本文主要阐述的是信号处理的算法实现,硬件部分的内容在此不再赘述。

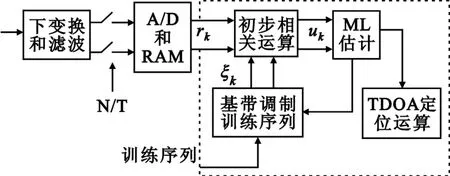
图2 相关定位接收机Fig.2 The correlation location receiver

3.1 信号到达时间的处理技术

由于是对移动台进行定位,所以必须截获被定位移动台的上行常规突发信号,在接收机完成对被定位移动台的上行常规突发RF信号的接收后,接收机中的DSP首先进行定位算法运算,确定信号的到达时间。

3.1.1 到达时间的初步判断技术

接收机中的A/D电路对滤波后的I、Q两路基带信号进行取样,取样速率为Rb(Rb为GSM的突发脉冲比特速率,即270.833 kbit/s),得到一个时间间隔为T的I、Q两路接收样值序列,记为{uI(k)}、{uQ(k)},且{uI,Q(k)=uI,Q(kT+t0)},其中,t0 为初始采样时刻。

采用已知训练序列26 bit的中间16 bit的GSM本地基带信号作为参考信号,取每一比特中一点为采样点,记为{rI(k),k=0,1,…,15},{rQ(k),k=0,1,…,15}。

计算参考信号与接收样值序列的相关函数

即在0< n ≤6范围内,训练序列自相关函数具有良好的自相关特性,若 n >6,这一特性不再满足,所以式中常数N的选择应考虑这一因素,N的选择应使得进行相关计算的接收序列样值尽量靠近序列的中部。

确定该突发点的突发定时 N′,即寻找 N′,使得接收信号中间部分的采样值和本地参考信号样值的相关函数达到最大,即:

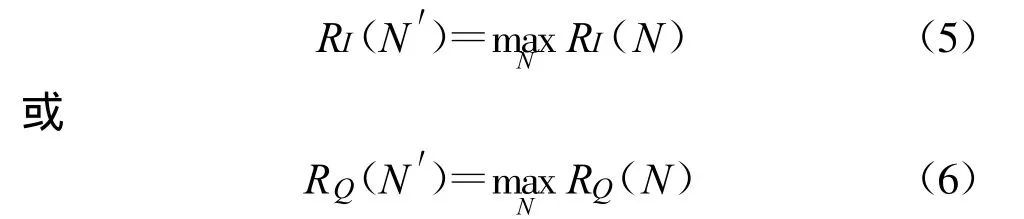
所以信号到达时间初步定为 t′0=t0+N′×(T/4),此时MLSE接收机与移动台实现同步,故此时间亦被称为信号有效接收时间窗。同时,利用GPS确定起始时间。

3.1.2 时延的ML估计处理技术

当接收时间窗初步确定后,为克服多径影响,采用最大似然估计ML算法[1],其本质是把对接收信号难以实现的多倍采样转化为对本地训练序列的多倍采样。具体叙述如下。

u(k)(uI(k)或uQ(k))为GMSK基带信号单倍抽样后的值,其中u(0)为训练序列中第6个比特起始时刻的值,u(k)的表达式为

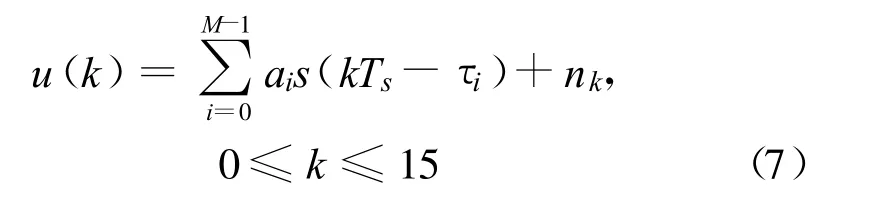
式中,M为信道多径数,ai为第i条信道的衰减因子,nk为复高斯白噪声,其协方差为 Cn,写成矩阵形式为

式中,U=[u0,u1,…,u15]T,A=[a0,a1,…,aM-1]T,N=[n0,n1,…,n15]T,

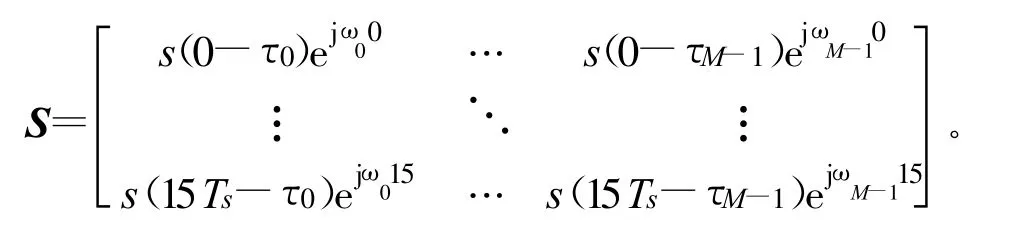
式中 ,τ=[τ0,τ1,…,τM-1]T为时延向量 ;ω为多普勒频移,在算法中不予考虑;Ts=T/N为对本地参考信号做N倍抽样后的抽样间隔。当N足够大时,时延 τi可以认为是Ts的倍数。另外,假定 nk是互不相关的,即E{nknHl}=0,k≠l。对于未知参数 τi和ai的最大似然估计就是求式(9)的最小值:

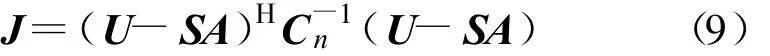
再假定已知信道的多径数目和每个信道时延值,即已知矩阵 S的情况下,则可以推算出要使J取最小值,A需满足:

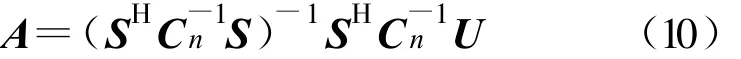
经过一系列的数学推算,可以求出J取最小值等价于式(11)取最大值:

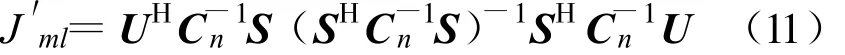
不失一般性,假定噪声为静态、均值为零、方差为N0的白高斯随机过程,那么 Cn=N0I,I为单位矩阵,则式(11)可表示为

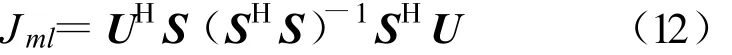
在S未知的情况下,算法要完成的就是以 Ts步长搜索可能的时延值,构造出 S来计算Jml,使Jml最大的时延值就是算法需得到的结果。

归结运算步骤如下:

(1)完成对uk的相关运算,求出I′值,得到矩阵 U;

(2)以 Ts为步长遍历时延向量τ的所有可能值,对每一种可能值,构造矩阵S;

(3)根据U和S可求出Jml。

找出使Jml最大的时延向量τ,则其中最小的时延分量τmin就是算法所要求的直达波的时延。

3.2 上行信号到达时间的确定技术

最后,根据获得的上行信号的 t′0和 τmin可确定出上行突发脉冲信号的到达时间:

用于定位的所用接收机均采用该方法确定被定位移动台的TOA,并将该参数送至定位中心。

当然,到达接收机的RF电波也有可能是反射、折射等非视距(NLOS)传播波,亦称为虚假目标电波,这时TOA测量中会存在一个附加超量延时,造成定位算法性能下降。工程实现中可采用Wylie算法进行NLOS误差鉴别、抑制和消除[2]。限于篇幅,关于如何提取真假目标作者将另文阐述。

4 定位算法中的方位信息处理技术

当TOA传到定位中心后,理论上依据双曲线方程则可求出移动台的位置,但是在实际中由于双曲线方程不是一组线性方程组,求解并不容易。经过比较,实际中采用了Fang算法[3-4]进行求解。该算法无需提供TDOA测量值误差的先验信息,算法简单明了,其定位估计值的模糊性可以通过蜂窝小区的有关信息来排除。该算法能得到基于TDOA测量数据的最优解。

TDOA的双曲线公式

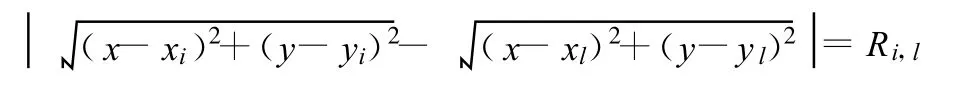
经过简化后可得:

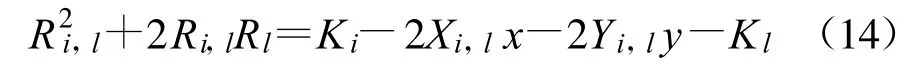
式中,Xi,l=Xi-Xl,Yi,l=Yi-Yl;Ri,l=cdi,l=Ri-Rl为信号达到接收机i和l之间的距离差,c为电波传播速度,di,l=TTOA,i-TTOA,l为接收机i和l之间的信号到达时间差;Ki和Kl为推导过程中出现的常数;Rl、x和y为未知数。

Fan算法利用3个接收机对移动台进行二维定位。为简化计算,将3个基站置于以下坐标系统:接收机1(0,0),接收机2(x2,0)和接收机3(x3,y3)。将坐标代入并经过一系列的推导后有[3]:

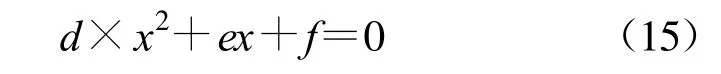
其中:

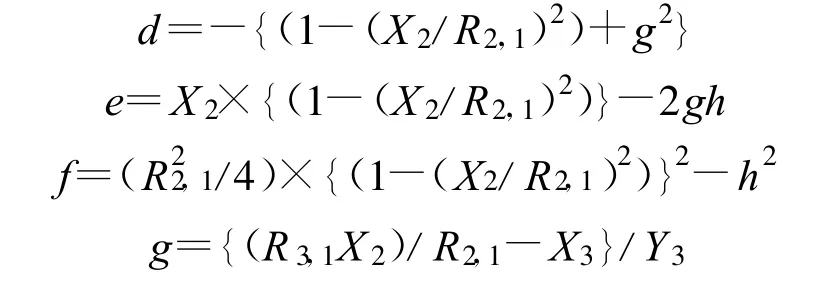
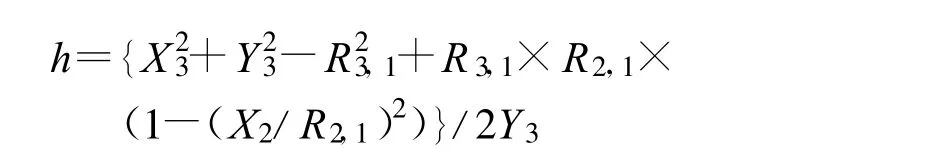
上面的方程有两个根,根据有关文献[3]的仿真结果,其中由根确定的移动台位置通常超出服务小区的范围,所以选择x=(-e-为解,将之代入式(14)中可以得到移动台的估计位置(x,y)。

5 定位算法的精度分析、实际测试结果及结论

5.1 定位算法的精度分析

精度分析基于误差分析的基础上,以无线信号的TOA进行定位得到的结果一般存在如下误差:

(1)无线电波在不同介质中传输速度不同造成的误差;

(2)移动台发射电路的频率稳定度造成的误差;

(3)信号是经过多径传输到达接收点的,即接收到的信号可能不是直达信号,则测得的时延不一定是直达信号的传输时延,即存在所谓非视距传播(NLOS)误差;

(4)即使存在直达路径,由于多径传输导致接收到的信号由多个路径信号合成,这时利用本地信号与接收信号进行ML估计时其相关峰值不一定出现在本地信号和直达信号的对齐处,出现步进误差。

第一种和第二种情况造成的误差一般在误差综合时加以考虑;对于第三种情况,如前所述,可以通过Wylie算法进行NLOS误差鉴别、抑制和消除;对于第四种情况,因误差与算法相关,本文作如下讨论。

当进行粗略的到达时间估计后,在ML估计时首先需将一个比特进行2L倍细化,即得到Ts进行步进。假定1个比特时间为T,在N倍采样的情况下,可能的时延误差就为(T/(L×N))。在GSM系统中,正常突发的1个比特时间为3.69 μ s,如采用4倍采样并进行反折后(即L=8,N=4),此时时延误差为(3.69/(8×4))=0.115 μ s,造成测距误差为(0.115×(3×108/106))=34.5 m。需要说明的是:由于 N不可能无限取高,且N达到一定数值后算法精度也不再提高,因此综合多种情况,实际工程中取N=4。

再结合第一种和第二种情况造成的误差和借鉴微波频段定位的经验值,利用时差得到的距离存在80 m左右的理论误差,因此具有较高的精度。

5.2 实测结果与结论

工程化时,利用DSP技术将如上算法固化在研制的GSM MLSE接收机中,形成专用的定位设备。在实际性能评估时,结合项目的需求,在典型市区、典型山区和典型平原这3种典型的环境下进行了测试。3台基于GSM系统的MLSE接收机和一部被测移动台在视距(LOS)的情况下经过100次测试后得到如表1所示的结果。

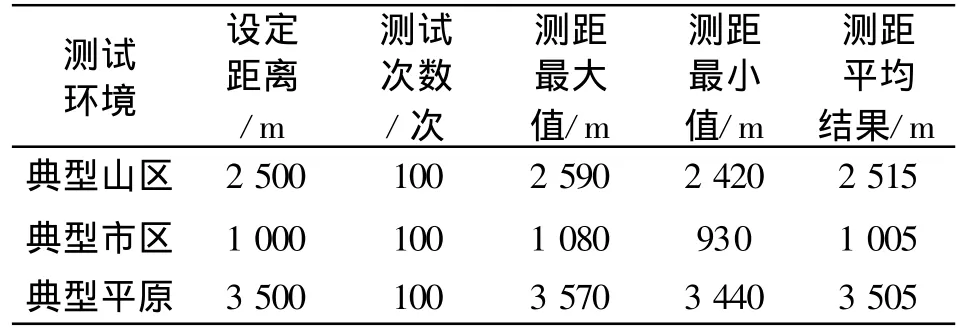
表1 测试结果Table 1 The test results

由表中数据比较可见:在平原环境下,由于无明显的多径效应且有直达波的存在,测试结果较为理想,误差较小,波动范围为±70 m;山区环境下,由于多径时延较为明显,测向定位误差较大,波动范围为±90 m;市区则处于中等水平,其波动范围为±80 m。实际测试结果与国内外相关实验室大量计算机仿真的结果[3,4]相比较,基本符合理论研究得出的结论。

目前,该算法已成功地应用于某大型军用系统中,实际使用效果表明该算法具有一定的应用价值。

[1] Saarnisaari H.ML time delay estimation in a multipath channel[C]//Proceedings of IEEE 4th International Symposium on Spread Spectrum Techniques and Applications Proceedings.Mainz:IEEE,1996:1007-1011.

[2] Wylie M P,Holtzman J.The non-line of sight problem in mobile location estimation[C]//Proceedings of 19965th IEEE International Conference on Universal Personal Communications.Cambridge,MA,USA:IEEE,1996:827-831.

[3] 范平志,邓平,刘林.蜂窝网无线定位[M].北京:电子工业出版社,2002.FAN Ping-zhi,DENG Ping,LIU Lin.The wireless location of the cell network[M].Beijing:Publishing House of Electronic Industry,2002.(in Chinese)

[4] Fang Bertrand T.Simple Solutions for Hyperbolic and Related Position Fixes[J].IEEE Transactions on Aerospace and Electronic Systems,1990,26(5):748-753.