基于参数估计精度的Bayes试验设计方案研究★

王囡，刘琦

（国防科学技术大学信息系统与管理学院，湖南 长沙，410073）

1 引言

装备试验设计就是根据试验的目的和要求，运用统计学原理，基于试验鉴定中的参数估计精度要求，合理选取试验样本，制定出优化的可行试验方案，以尽可能少的试验次数来获取足够有效的数据或资料，对试验结果作出推断，对战技指标进行评价，得出比较可靠的试验结论[1]。装备战术技术指标 （参数），如可靠度、命中率和可用度都是装备作战适用性的重要度量标准。对战术技术指标（参数）的评估通常是依据统计学原理，从总体中选择样本进行试验，然后根据试验结果进行统计推断，从而给出参数的估计值。该方法导致了参数估计的精度在很大程度上依赖于抽样时样本量的大小。通常情况下，样本量越大，对参数的估计[2]就越精确。那么在试验中到底选择多大的样本量才能满足参数估计的精度要求，这就是基于参数估计精度要求的试验方案设计需要解决的问题。

基于参数估计精度要求的装备试验设计方案可以定量地为装备试验提供一个实施试验的标准，从而在工程中得到了广泛的应用。在经典统计学领域，Charles R.Allmen等[3]基于Weibull分布，给出了在不同的置信水平及试验时间下，可靠性试验需要的样本量；Ming-Wei Lu等[4]对基于置信水平要求的Weibull分布验证试验设计方法进行了分析，在给定置信水平的条件下，推导出了试验时间的计算方法；武小悦等[1]给出了正态分布条件下基于参数估计精度要求的样本量计算方法；崔卫民等[5]研究了试验数据服从双参数Weibull分布时，在一定精度指标和置信水平下，如何确定估计特征寿命和安全寿命时所需的最少试件数。

随着装备技术含量的增加，其研制、生产和试验费用日趋昂贵，基于经典统计方法进行试验通常需要较大的样本量，这在试验实施中通常是不可行的。因此，需研究装备在小子样条件下的试验设计。武器装备在进行现场试验之前，通常有大量的验前试验信息可供利用。Bayes由于能综合利用各种验前信息而在武器装备试验鉴定中得到广泛的应用[6]。因此，研究利用Bayes方法进行试验设计具有重要的实际工程应用价值。在小子样条件下，利用Bayes方法对产品的试验方案进行设计，已有部分学者进行了研究。如在基于两类风险 （使用方风险和生产方风险）需求的试验试验设计方面[2]，Amrit L.Goel等[7]针对寿命服从指数分布的情况，基于两类风险要求，研究了试验时间与失效数的关系；Ming-Weilu等[8]基于置信水平 （参数的验后概率）要求，给出了失效数为零时的样本量求解方案；张硕云等[2]对方差已知正态分布情形下的装备Bayes试验设计方案进行了研究，基于两类风险给出了试验样本量的计算公式。在基于参数估计精度要求的试验设计方面，冯广斌等[9]考虑失效数为零时，通过给定置信水平及系统可靠度，得到了试验样本量的计算方法。但没有给出参数估计精度要求的通用描述，并且仅对指数分布零失效的情况进行论述，没有将结果进行推广。

本文基于参数估计精度要求，对装备试验设计的需求进行了分析。对基于Bayes方法的二项分布装备性能指标验证试验设计方案进行了分析，建立了基于参数可信区间要求的试验方案求解模型，给出了现场试验样本量的计算公式及MATLAB计算算法。最后，结合实例进行了理论和算法的验证。

2 基于参数估计精度的装备试验设计需求分析

Bayes方法通过对验前分布与现场信息的综合，对验后分布参数进行估计，其未知参数为随机变量，具有某种分布。当采用Bayes方法进行参数估计时，需要满足一定的精度要求，如绝对精度要求、相对精度要求等[10]。设装备试验评价中，要估计的参数θ的验后分布为π (θ|X)，其中θ根据评价指标的不同可分别表示为可靠性度、命中概率、成功率等；X为装备的现场试验数据。π(θ|X)的分布密度如图1所示，且Bayes方法中的参数精度要求可定义如下。

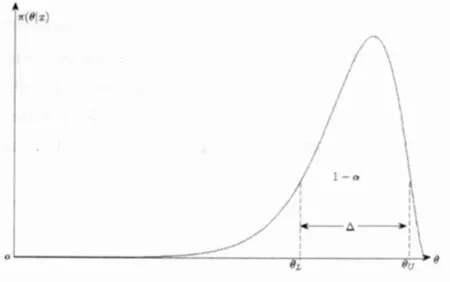
图1 参数估计精度示意图

a）绝对精度要求

绝对精度是指在一定的验后概率要求下[10]，如在验后概率1-a（等价于经典统计方法中的置信水平）要求下，要求参数θ的Bayes可信区间[11]的宽度小于等于某一给定的值，即

△——参数估计精度要求的区间宽度。

由验后分布的概率表示为：

b）相对精度要求

相对精度是指待估计参数的绝对精度与参数验后均值的比值。在验后概率1-α要求下，要求参数θ的Bayes可信区间的相对宽度的一半不大于某一给定值，即

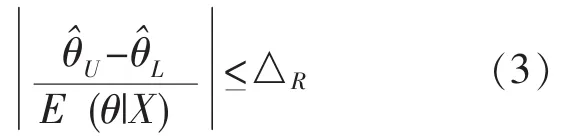
式 （2）中：E(θ|X)——θ的验后期望；

△R——给定的相对精度要求。

由于在试验设计阶段E(θ|X)通常未知，所以可由历史信息等给出E(θ|X)的估计值。相对精度要求由验后分布的概率表示为：

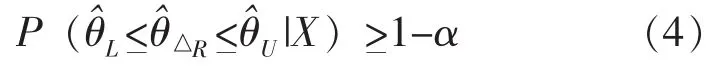
相比绝对精度要求，相对精度要求考虑验后期望，从而容易度量参数估计的结果与实际值之间差异的大小，从而便于精度估计之间的比较。

由于绝对精度求解简便且可以定量地为试验装备提供一个评价标准，便于工程试验判定；且从统计学角度而言，两个参数估计精度要求之间可以通过式 (1)和式 (4)互相转换[10]。故本文仅基于绝对精度要求，对小子样条件下的装备试验设计进行分析研究。

3 成败型装备的试验设计方案求解

在装备试验评价中，二项分布是一个非常重要的分布类型，而且很多装备的试验结果是成败型的，如飞航导弹的飞行试验命中精度[12]，引信的发火可靠性[13]等，因此，下面以成败型试验为例，对基于参数估计精度要求的试验设计方案求解过程进行说明。

设X=（X1，X2，…，Xn）是服从于参数为 p的成败型分布的独立同分布样本，其中p表示成功概率，未知，记表示第i次试验成功，Xi=0表示第i次试验失败，则s为n次试验中的成功试验次数，记f=n-s为n次试验中的失败试验次数。从而可得似然函数为:

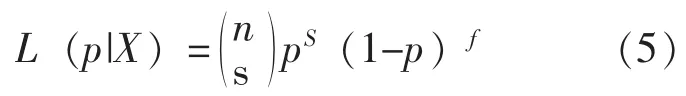
设p的验前分布为Beta分布B （α0， β0） （为p的共轭分布），其密度函数为：

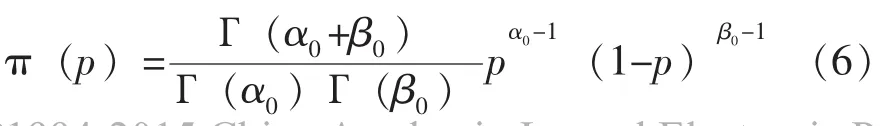
式 （6）中：α0——表示伪成功数；

β0——表示伪失败数，可由验前信息计算得出。

p的验后分布π （p|X）仍为Beta分布[14]，记为 B （α1， β1）：

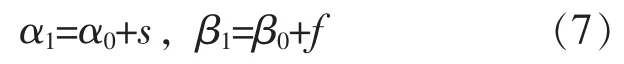
试验设计要求为在验后概率 （即可信水平）1-α下，要求参数p的可信区间之间的宽度不大于△，即

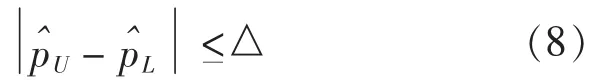
上式等价于：

对于成败型产品基于参数估计精度要求的试验设计而言，就是在选择满足式 （9）要求的最小的n。由于式 （9）中有两个未知参数 （n、s或者n、f），所以试验设计就是在给定f或者s的条件下，选择满足式 （9）要求的最小的n。

在参数的区间估计中，HPD（High Posterior Density）可信区间是所有的可信区间估计中，区间宽度最短的可信区间。

Beta分布的密度函数是单峰连续但不对称的，因此，它的HPD可信区间不是等尾可信区间，难以写出其解析表达式。可用逼近算法选择不同的n、f进行逼近，求出p的 （1-α）HPD可信区间，然后根据式 （9）选择满足要求的n、f。但本文主要目的在于阐述基于Bayes方法的试验设计，故可用等尾可信区间来表示p的区间估计，求p的（1-α）等尾可信区间。此时的满足如下积分公式：

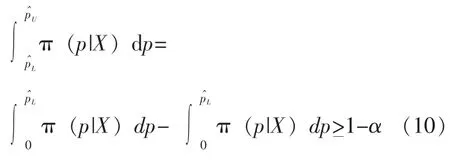
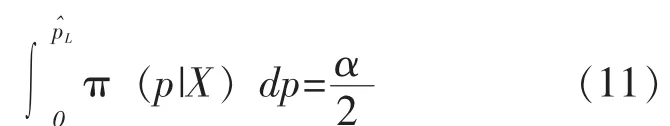
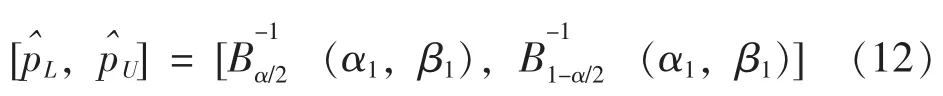
对于规定失败数，满足式 （9）要求的样本量n（记为nT，表示试验需要的样本量）为：

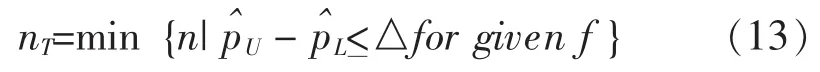
在计算时，可将n从f开始进行逐个迭代，即选择n=f，f+1，…，依次代入式 （13）进行判断，然后选择合适的nT即可。

4 实例分析

根据电子系统试验场所做过的雷达发现概率试验[15]，从历史资料中查到了相关有效的 “历史数据”，运用Bootstrap法求得其验前分布为Beta分布 B （α0， β0）， 其中 α0=67.0912， β0=1.2273，试在给定验后概率1-α=0.90，区间宽度为△=0.036的要求下，设计一个试验方案，在不同的规定失败数下，确定现场所需的试验样本量。

结合公式并应用MATLAB算法，求得在规定失败数f时，试验所需的最小样本量，如表1所示。

4.1 数据分析

通过给定不同的规定失败数f，得到在不同可信验后概率要求下的最小样本量，根据对表1的分析，可得出如下结论：

a）当失效数相同时，可信验后概率越高，现场试验所需的最小样本量越大。工程意义为装备的参数评价时要求的可信验后概率越高，试验所需的样本量越大。

表1 二项分布试验设计结果

b）在同一可信验后概率下，规定失败数越大，装备所需的最小样本量越大。工程意义为装备试验中要求得到的失败数越大，试验所需的样本量越大。

4.2 图形分析

根据表1，选取可信验后概率为0.9，规定失败数分别为0和1的情况，绘制成功概率р的验前分布密度函数曲线和验后密度函数曲线，如图3所示，分析图形可得出如下结论：

a）在同一验后概率1-α下，综合利用验前信息与现场试验信息估计参数的验后分布，所估计的总体参数可信区间宽度会变窄，精度变高。

b）在验前信息相同时，现场试验的样本量越大，所估计的总体参数的可信区间宽度越窄，参数估计的精度越高。

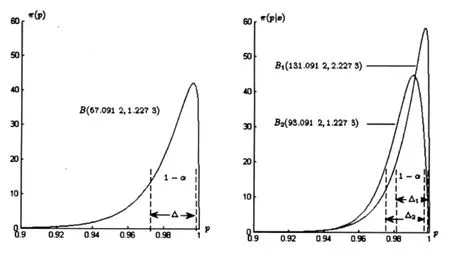
图3 Beta分布密度曲线图

5 试验设计方法的使用说明

装备试验过程中规定失败次数的确定要综合考虑试验成本、故障模式及可靠性指标等因素。例如，试验中的规定失败数越大，试验过程中所得到的故障模式就越全面，就能更加合理地满足产品的可靠性指标要求，但试验过程所需的试验成本也随之增加。反之，产品的故障模式及可靠性指标不能得到很好的检验，却能够节约试验成本。

对装备试验设计而言，本文所提供的试验设计方案的具体使用方法如下：

a）装备试验人员根据可信验后概率要求、区间宽度及规定失败数，查询表1（表1可利用本文提供的程序不断完善、扩充）。若能查询得到数据，则以此作为试验中的最小样本量；若不能查到，则通过本文所提出的算法进行计算，从而得到试验所需的最小样本量。

b）将所得的最小样本量作为试验样本量。当所有的样本试验完毕时，若试验失败数小于等于可接受的规定失败数，则试验装备达到可信验后概率要求；反之，未达到。

c）将所得的最小样本量作为判定依据。当试验中出现了规定失败数时，若试验样本量大于等于最小样本量，则试验装备达到可信验后概率要求；反之，未达到。

d）在Bayes分析中，共轭验前分布的选择简化了整个计算过程。在选取过程中，应保证选择的验前分布满足产品信息的寿命分布及验前信息的可靠性、合理性等要求，即验前分布的选取应以合理性作为首要原则。

5 结束语

本文对基于参数估计精度要求的Bayes试验设计方案进行了方法研究，具体工作包括：

a）论文对基于Bayes方法的参数估计精度要求进行了详细的阐述。并针对具有二项分布性能产品的情况，建立了参数可信区间的求解模型，对基于Bayes方法的试验设计方案进行了理论研究推导及算法实现，解决Bayes可靠性试验设计计算难的问题。

b）本文仅对等尾可信区间的情况进行了分析说明，公式的推导及算法设计过程比较容易实现。但在实际的装备试验过程中，非等尾可信区间情况的存在较为普遍，其求解过程需要逐次逼近，进而求得最优解。这个求解过程比较复杂，还没有给出成熟的解决方案，可作进一步的研究。

[1] 武小悦,刘琦.装备试验与评价 [M].北京:国防工业出版社,2008.

[2] 张硕云,武小悦,刘琦.基于两类风险的正态分布Bayes试验样本量 [J].航空计算技术,2008,(5):11-13+17.

[3] CHARLES R A CORPORATION.C Sample size for failure detection and reliability demonstration[C]//Reliability and Maintainability Symposium.1993.

[4] MING W.,R.R.J.Laboratory reliability demonstration test considerations.Transactions on Reliability[J].2001,50(1):12-16.

[5] 崔卫民,薛红军,喻天翔,等.试验数据服从Weibull分布时可靠性试验最少试件数的确定 [J].机械工程学报，2008,(1):51-55.

[6] 张金槐,刘琦,冯静.Bayes试验分析方法 [M].长沙:国防科技大学出版社，2007.

[7] AMRIT L G.Design of reliability test plans based Upon prior distribution[R].Final Technical Report,1978，12-200.

[8] Ming W.,R.J.Rudy.Reliability demonstration test for a finite population.Quality Reliability. [J].2001,(17):33-38.

[9] 冯广斌,钱林方.应用贝叶斯方法进行系统可靠性验证[J].兵工学报， 2004,(2):178-181.

[10] 武小悦,刘琦.应用统计学 [M].长沙:国防科技大学出版社，2009.

[11] 茆诗松.贝叶斯统计 [M].北京:中国统计出版社，1999.

[12] GJB 2899-1997,飞行导弹飞行试验精度分析和命中精度评定方法 [S].

[13] 中国人民解放军总装备部军事训练教材编辑工作委员会.可靠性试验技术 [M].北京:国防工业出版社，2003.

[14] LEONARD T,HSU J S J.Bayesian methods[M].Cambridge:Cambridge University Press,1999.

[15] 王国玉,申绪涧,汪连栋.电子系统小子样试验理论方法[M].北京:国防工业出版社，2003.