频率测量研究综述

陈丽锋，孟瑞，冯希

(中国地质大学机电学院，湖北武汉430074)

随着电子技术的发展，对频率测量的要求越来越高，如何如提高频率测量精度，使测量频率范围加宽，使频率测量能高速可靠自适应的进行，是迫切需要解决的问题，也成为学术界的研究热点。

频率测量误差主要来自±1个字计数误差和时基误差。时间间隔测量误差主要来自±1个字计数误差、时基误差、触发器误差和系统误差。±1个字计数误差是指当电子计数器进行一次测量时，会存在一个以最小有效数字为单位的±1个字计数模糊度—量化误差，技术模糊度存在的原因是计数器时钟频率与输入信号的不一致。时基误差是时基晶体振荡器的实际频率与其标称频率的不同所导致的误差会被直接转化为测量误差。触发器误差是指由输入信号的噪声和来自计数器输入通道的噪声所产生的随机误差。系统噪声则是开始通道和停止通道放大器的上升时间和传播延迟的极小不匹配等引起的。各学者利用新算法、新技术降低误差来优化频率测量技术。

1 直接测频法

林敏等［2］，2000年根据小波包变换的优良时频分析能力，引入阈值熵来定量地描述瞬时信号在时频空间中的分布，提出了在强噪声背景下，检测瞬时信号的到达时间和频率成分的方法。信号和噪声有截然不同的小波特性，随着分辨尺度的减小，信号的特征将越来越明显而噪声成分却相对减弱。经小波包分解后的各子频带内的小波系数，其模极大值的幅度由信号的频率成分决定，而模极大值的位置是由信号到达时间决定。这种基于正交小波包的瞬时频率检测方法简单、可靠、易于检测，可广泛应用于奇异性检测、瞬时信号定位、动态测试和故障诊断等领域。

章军等［2］，2003年提出了一种多周期同步测频的改进方法，该方法继承了多周期同步测频法的优点，同时提高了测量精度。多周期同步测频技术的闸门时间与被测信号同步，消除了对被测信号计数产生的±1个字的误差，使测量精度大大提高，且测量精度与被测信号频率无关，在全频段内测量精度是均衡的。影响多周期同步测频精度的主要因素是对标频信号的计数仍存在±1个字的误差，在不提高标频频率和闸门时间的前提下用两个计数器分别对标频上升沿和下降沿计数，再把2个计数结果进行算术平均作为修正后的计数结果，可以使误差率减少1/2。

孙进才等［3］，2005年为了提高信号的相位匹配原理估计正弦信号参数的精度，提出了一种正弦信号频率、振幅和相位参数的最小二乘估计法，并改变了序列选取方法，不再为求信号而做近似，消除估计信号中的奇异峰和噪声对被估计信号的影响。这种方法无需估计参量的先验概率密度函数或最大似然函数，且只需一次观察就可以实现信号频率、幅值和相位估计。这种方法不仅能降低估计频率带宽以外的噪声，还可降低被估计频率信号带宽内的噪声，提高低信噪比时参数估计精度。

李伟等［4］，2006年提出了一种测量低频信号频率的方法。利用高速数据采集器采集周期信号，基于最小二乘法原理，在曲线过零点附近用直线拟合，求得过零点坐标，然后利用基于电子计数器的测周法计算出频率。这种方法用于测量频率0.005～10 Hz的正弦信号、方波、三角波等，其测量精度可达到10－5Hz，这种方法取频率的工作量仅为FFT的1/2。

2 时间间隔—相位转换测频法

周渭［5－6］，1993年对相位重合点检测技术进行了研究。提出了一种既有宽频率范围又有高测量精度的相位重合点检测技术——相检宽带测频技术。两个任意周期信号之间的相位差会随时间呈周期性变化，其周期是两周期信号间的最小公倍数周期，其频率是两周期信号的最大公因子频率。将相位差按大小顺序重新排列后，其中一些相位差值远小于两个信号的周期的点称为相位重合点。当两个中高频频率间的最大公因子频率较小时，相位重合点所代表的相位差会在约几ps到十分之几ns，以这样的相位重合点间的时间间隔构成测量闸门时间时，大大降低了±1个字计数误差，这种用相检方法捕捉相位重合点实现宽频率范围测量的方法称为相检宽带测频技术。其频率测量易获得10－10/s～10－11/s的测量精度。测量的闸门时间信号，受仪器的参考闸门时间及标频信号与被测频率信号的相位重合点共同控制，当被测频率信号与标频频率值接近或互成倍数关系时，可借助频率合成器，合成一个与标频信号频差不大的另一个频率信号，代替标频对被测信号进行测量。但这种高精度的测频技术存在测频下限的问题，采用5 MHz标频测量时的测量下限在10 kHz以上。针对更低下限频率的测量，为使频率合成器有更好的频率稳定指标和更合理的频率值，使标频信号及被测信号分别与公共振荡器进行相位重合点检测，检出它们与公共振荡器信号之间时差很小时的相位重合点，参考闸门时间与两组相位重合点信号分别作用产生两个测量闸门时间信号，这种用双相检方法捕捉相位重合点实现宽频率范围测量的方法为双相检宽带测频技术，其测量范围为几kHz到数百MHz。这种方法测量精度高，测量频率范围宽，设备构成简单，广泛应用于时频测量领域。

潘继飞等［7－8］，2007年提出了一种时间—相位转换方法，是对以电子计数法为基础的原理误差T1和T2进行二次测量，将对时间的测量转换成对幅度的测量，从而通过幅度进行相位提取，得到时间T1和T2，即将T1和T2的测量转换为对基准信号的相位测量。此方法不存在原理误差，可以完成时间间隔的连续测量，时间测量范围大且测量精度高，理论测量精度可达ps量级。其测量原理图如图1示，图中TOA为脉冲到达时间，ADC为模数转换。

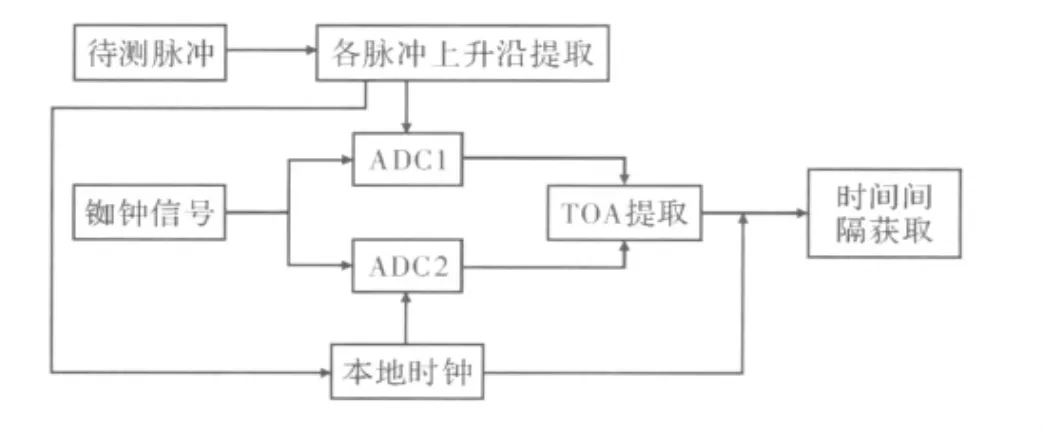
图1 基于时间—相位转换的高精度时间间隔测量原理

王海等［9］，2008年针对高精度的频率测量，分析了相位检测法的测量误差，根据分析结果提出并实现了一种基于FPGA实现的频率测量方法。该方法利用FPGA器件门时延小、电路稳定的特性，采用相位重合检测的改进方法，有效降低了闸门时间误差，即降低测量时的±1计数误差，提高了频率测量精度，其测量精度约为10－11/τ量级，比原实现方法高6～8倍，能够满足高精度、低成本的频率测量要求。

梁文海等［10］，2008年通过对直接频率测量、等精度频率测量的测量误差及产生原因的分析，并根据周期性信号之间的规律性相位差变化特性，提出了一种实现高精度频率测量的具体实现方案。直接频率测量的测量速度快、精度高，但在相同闸门时间直接测量的相对误差测量，会随着被测信号频率的变化而变化，而等精度频率测量误差只与闸门时间及标准频率有关，没有提高测量精度。通过同步检测，使被测信号和标准频率与闸门同步，解决了等精度频率测量中闸门信号只与被测量信号同步，对标准频率的±1计数误差仍存在问题，测量时通过相位同步检测电路，被测信号与标准频率的相位重合点，进一步产生与被测信号和标准信号都同步的闸门信号，从而实现频率的高精度测量。

杜保强等［11］，2010年提出了一种基于异频相位处理的高精度频率测量系统的设计方案。在异频鉴相技术的基础上，通过脉宽调整电路，减少相位重合点簇中的脉冲个数和附加相位控制电路，有效捕捉最佳相位重合点，在此相位重合点建立测量闸门，克服了传统频率测量中存在的±1个计数误差，进而提高测量精度。此方案结合现场可编程门阵列(FPGA)片上技术，既保留了相位重合检测技术客服±1个计数误差的优越性，同时也提高了测量速度、简化了测量设备、降低了成本和功耗。其实际测量精度可达10/s量级，明显优于传统测频方法的测量精度。其系统原理框图如图2所示。

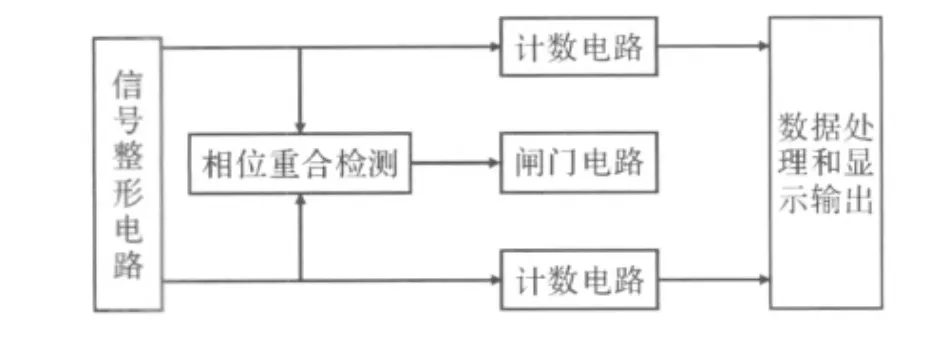
图2 异频相位重合检测原理

3 数字化测频法

国彬等［12］，2008年对等精度频率测量方法进行了两方面的改进，一方面在不提高系统频率和延长测量门限时间的前提下，通过对基准时钟信号计数值的修正，用两个计数器分别对基准时钟信号上升沿和下降沿计数，再将2个计数结果进行算术平均作为修正后的计数结果，改进后的方法较原方法测量结果的相对误差减少了1/2，进一步提高了测量精度。另一方面利用对被测信号的自适应分频，消除了预置门限时间带来的不足，简化了同步逻辑电路，提高了系统的可靠性，实现了测量门限时间的自动寻优，在基于可编程逻辑器件CPLD以及DSP芯片的硬件系统中，实现范围为1 Hz～2 MHz、相对误差≤10－4的频率测量。

杨秀增［13］，2009年采用了SOPC设计结构，用Niosll软核CPU运行自适应算法，使测量时间达到最优，并将优化后的等精度测频IP核，通过用户自定义逻辑组的方法添加到系统中，从而构建一个单片的基于NiosⅡ的自适应高精度频率测量系统。他分析了等精度频率测量基本原理，并对等精度频率测量原理进行优化，给出了优化的等精度频率测量原理图，介绍了等精度测频IP核设计方法，给出了此核的Verilog HDL程序。通过分频50 MHz的系统时钟得到各种测试信号，并给出了0.1 Hz～50 MHz的测试结果，这种方法有效克服了测频逻辑功能模块与控制器相分离的缺点，提高了系统的精度，此系统工作稳定可靠、测频精度高，最大相对误差在10－7/s级别。

汪之国等［14］，2009年为了减少普通电子计数法测频时的±1量化误差，采用数字滤波滤除量化噪声，设计了一种基于快速滤波的高精度测频电路。使用FPGA器件和VHDL语言设计了测频系统，用信号发生器所产生的标准信号测量结果表明快速滤波基本消除了量化误差的影响，实现了高速、高精度测频。

4 内插测频法

潘继飞等［15］，2006年提出了一种基于内插采样技术的高精度时间间隔测量方法。该方法对原理误差的测量转变及对基准信号相位的测量，完全克服了传统时间间隔测量原理误差，并解决了测量范围和测量精度的矛盾，能够完成实时测量，且其时间间隔测量精度能够达到十皮秒级。这种方法是将时间零头T1和T2的测量转化为对基准信号相位的测量。T1=待测脉冲间隔PRI=(n－m)T0+T1－T2=TOA1－TOA2，其中m、n是计数器输出值;f0是基准信号频率;φA、φB、φC、φD是内插采样点相位;TOA是脉冲到达时间;T0为量化时钟周期。原理结构简图如图3所示。

图3 基于内插采样技术的时间间隔测量原理结构图

刘永刚等［16］，2010年针对弱信号条件的频率精确测量问题，在现有时域和频域方法的基础上，基于数字式内插法能够兼顾实现时域插值和同步实现频域测量的特点，提出了一种新的数字式时频域频率测量系统，系统利用频域方法得到信号的粗略频率，根据粗略频率值构造跟踪滤波器对原波形进行滤波，然后在时域进行软件插值，即可得到信号的精确频率。这种新的时域和频域相结合的算法，实现了一种数字式实时高准确的频率测量系统。频率测量系统算法流程如图4所示。

图4 频率测量系统算法流程

5 混频测频法

边玉敬等［17］，1991年提出了一个适于多个频标相位和长短期频率比对的高精度测量系统，即基于双混频时差测量原理的多路ns时差自动测量系统。这种测量方法突破传统时间比对法的计数器分辨力和分频器相位抖动的限制，使相位测量的分辨力进展到皮秒或更小的量级，由此导出的短长期频率测量精度与频标表现出的最高性能相匹敌，且其取样时间的选取比较灵活，相邻频率取样完全无间隙。当比对信号采用5 MHz，与一个分辨力为1 ns的计数器相配，时差测量的理论分辨力为0.2 ps。

黄斌等［18］，1995年提出一种从宽带噪声中提取未知频率窄带信号的方案，该方案采用单滤波器与数字式频率扫描锁定系统相结合的方法，经混频后，与低速模拟/数字转换器和FFT配合，对高频信号实现细化的谱分析，此方法可提取0～26 MHz内的未知单频信号，并改善信噪比约18 dB，其工作原理原理如图5所示。

图5 工作原理框图

张彦龙等［19］，2008年针对深空USB测控系统的高精度侧音测距需要，提出了一种基于频率测量和二次混频的高精度数字锁相环实现方案。其由高精度测频、数字混频、滤波抽取、二阶数字锁相环等模块组成，在输入载噪比为25 dB·Hz，多普勒频偏为±300 kHz时工作稳定。数字锁相环由DPD、DLF、NCO等基本单元组成，输入信号被采样并与环路输出的本地载波进行相位比较，产生一个可以充分反映两者相位误差大小和极性的数字样本序列，再经过数字环路滤波器加以平滑得到控制信号对本地NCO进行控制。实现结构如图6所示。

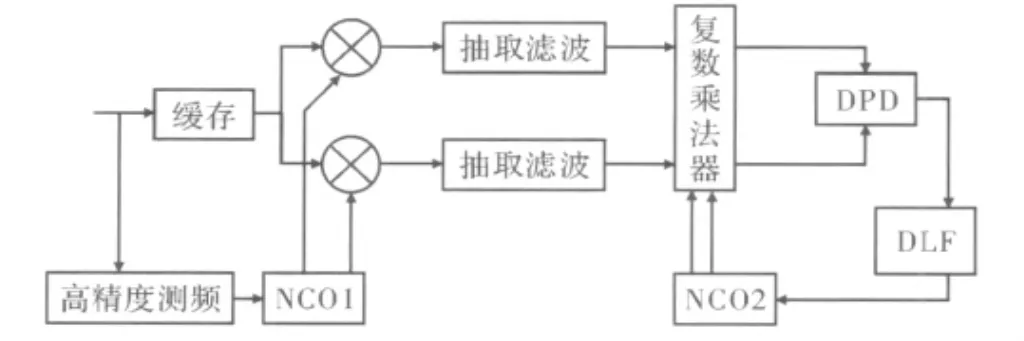
图6 高精度锁相环的实现结构

徐闽斌等［20］，2010年提出了一种适用于电磁波电阻率测井的微弱信号相位检测方法，利用基于DSP和FPGA对接收的微弱信号，实现高精度的相位检测，该相位检测方法有较高的噪声抑制能力，测量误差精度高达10－7/s量级。

刘进等［21］，2010年针对直接利用随机共振原理不能有效地检测出大频率微弱信号的问题，提出了利用混频器的频谱搬移特性，将待测的大频率信号和信号发生器产生的信号混频，从而使大频率信号转换为小频率信号，然后再加入非线性双稳态系统，能有效地检测出大频率微弱信号。原理框图如图7所示［22］。

图7 混频随机共振原理框图

6 频率测量方法分析及总结

文中通过对前人频率测量研究成果的分析和总结，对频率测量有以下几点认识:

(1)频率测量是一项基本且重要的测量技术，各学者对频率测量的研究主要分为5类:直接测频法、时间间隔/相位转换测频法、数字化测频法、内插测频法和混频测频法。直接测频法是用新算法对频率进行测量，时间间隔/相位转换测频法是利用相位重合点检测技术将对频率的测量转化为对相位的测量，数字化测频法是利用现场可编程门阵列使频率测量能高速可靠地进行，内插测频法利用内插法完全消除频率测量原理误差的优点来进行高精度频率测量，混频测频法利用混频技术使待测频率和标频相匹配来实现高精度频率测量。

(2)结合各学者的频率测量研究成果，将各频率测量方法的优点和缺点总结如表1所示。

表1 各频率测量方法的优点和缺点

(3)随着微电子工艺的发展和可编程器件性能的提高，FPGA在逻辑容量、工作频率、体积、可靠性、灵活性、软件开发环境、在线可编程等优势，使得利用FPGA完成电子线路设计成为一种趋势。基于可编程逻辑器件的高精度频率测量将得到进一步的发展，将并行通道集成在同一芯片中进行测量，利用内插器的非线性修正、利用锁相环和DSP技术进行频率测量也将成为趋势。频率测量仪将逐步实现自动化，使频率测量的一致性更好，利于减少误差，提高测量精度。

［1］ 林敏，陈希武，周兆经．基于正交小波包的瞬时频率检测［J］．计量学报，2000，21(3):227－231．

［2］ 章军，张平，于刚，多周期同步测频测量精度的提高［J］．电测与仪表，2003(6):16－18．

［3］ 孙进才，朱维杰，孙轶源，等．正弦信号参数估计的最小二乘算法［J］．哈尔滨工程大学学报，2005(1):19－23．

［4］ 李伟，石超．一种软件测量低频正弦信号频率的方法［C］．桂林:2009年全国虚拟仪器大会，2009．

［5］ 周渭．相检宽带测频技术［J］．仪器仪表学报，1993(4):358－348．

［6］ 周渭．时频测量的新技术－相位重合点检测技术［J］．宇航计测技术，1993(3):61－73．

［7］ 潘继飞，姜秋喜，毕大平．基于内插采样技术的高精度时间间隔测量方法［J］．系统工程与电子技术，2006，28(11):1633－1636．

［8］ 潘继飞，姜秋喜．一种高精度时间间隔测量方法及仿真验证［J］．光电技术应用，2007(22):71－72．

［9］ 王海，周渭，宣宗强．高精度频率测量技术及其实现［J］．系统工程与电子技术，2008，30(5):981－983．

［10］ 梁文海，麦文，张健，等．一种高精度频率测量的研究与实现［J］．四川师范大学学报:自然科学版，2008，31(3):376－378．

［11］ 杜保强，周渭．基于异频相位处理的高精度频率测量系统［J］．天津大学学报:自然科学版，2010，43(3):262－266．

［12］ 国彬，张和生．基于CPLD与DSP的高精度自适应频率测量方法的研究与实现［J］．计算机测量与控制，2008，16(12):1814－1817．

［13］ 杨秀增．基于Niosll的自适应高精度频率计设计［J］．仪器仪表装置，2009(7):13－17．

［14］ 汪之国，龙兴武，王飞．高精度测频方法及其在四频激光陀螺中的应用［J］．传感技术学报，2009，22(10):1526－1528．

［15］ 潘继飞，姜秋喜，毕大平．模拟内插法及其测量误差分析［J］．电光与控制，2007，14(1):147－150．

［16］ 刘永刚，孟真，阎跃鹏．高准确度数字式时频域实时频率测量系统［J］．电讯技术，2010，50(9):28－32．

［17］ 边玉敬，陈淑芳，王丹妮．多路纳秒时差自动测量系统的研制［J］．宇航计测技术，1991(5):44－49．

［18］ 黄斌，范录宏，周正欧．宽带噪声中未知频率窄带信号的提取［J］．电子科技大学学报，1995(S2):188－191．

［19］ 张彦龙，王世练，王培慈，等．新型频率辅助高精度数字锁相环的设计与实现［J］．电子工程师，2008(6):15－17．

［20］ 徐闽斌，李建新，杨天池．微弱信号的相位检测技术研究［J］．信息工程大学学报，2010(1):40－44．

［21］ 刘进，赵文礼，夏炜．基于随机共振原理的大频率微弱信号检测方法研究［J］．机电工程，2010，27(1):11－14．

［22］ 李孝辉，杨旭海，刘娅，等．时间频率信号的精密测量［M］．北京:科学出版社，2010．