大范围运动刚柔耦合系统动力学建模与仿真
杨正贤,孔宪仁,廖 俊,徐大富
(哈尔滨工业大学 卫星技术研究所,哈尔滨 150080)
0 引言
随着航天器、机器人等机械系统朝着轻质、高速、高精度方向发展,具有轻质柔性部件的刚柔耦合系统大量出现。以往对这类刚柔耦合系统的控制研究多是基于传统零次近似动力学模型[1-2]。这种建模方法直接使用结构动力学中的变形假设,忽略了大范围运动和弹性变形的耦合项,而且没有考虑大范围运动对弹性变形运动的振动频率和振型模态的影响。当系统存在大范围刚体运动特别是高速运动时,零次近似动力学模型已不能正确揭示刚柔耦合系统的动力学行为[3-4],所以有必要研究更符合实际的精细动力学模型。
近年来,许多学者[5-10]从连续介质力学的基本原理出发,提出了较零次近似动力学模型更为精确的一次近似耦合动力学模型,并通过实验验证了零次近似模型的局限性和一次近似模型的准确性。但是该类模型都是从精细动力学分析需求的角度出发,在变形位移场和应力-应变中保留高阶项,导致动力学模型越来越复杂并引入大量强非线性项。这对于控制器的设计来说是不利的,增加了其设计和实际应用的难度,因此有必要建立适合刚柔耦合系统控制器设计的一次近似耦合动力学模型。
本文针对中心刚体加旋臂梁的系统,首先利用Hamilton原理建立了偏微分的一次近似耦合动力学模型,然后采用有限元法对其离散得到常微分形式动力学模型。该模型在变形位移场描述中计及二次耦合项,同时忽略轴向拉伸量,使得在引入动力刚化项时,简化了动力学模型。仿真结果表明,该精简模型正确预示了系统的动力学行为,能够用于实际控制系统设计。
1 刚柔耦合动力学模型
图1为带有大型柔性附件的典型刚柔耦合系统模型。模型包括一个中心刚体和一个均匀悬臂梁式柔性附件。中心刚体在平面内绕固定点ON旋转,柔性梁固结在中心刚体OB上。假设柔性梁为小变形小应变下的等截面Euler-Bernoulli梁,材料均匀且各向同性。这种模型在航天、机器人等领域有广泛的应用背景。
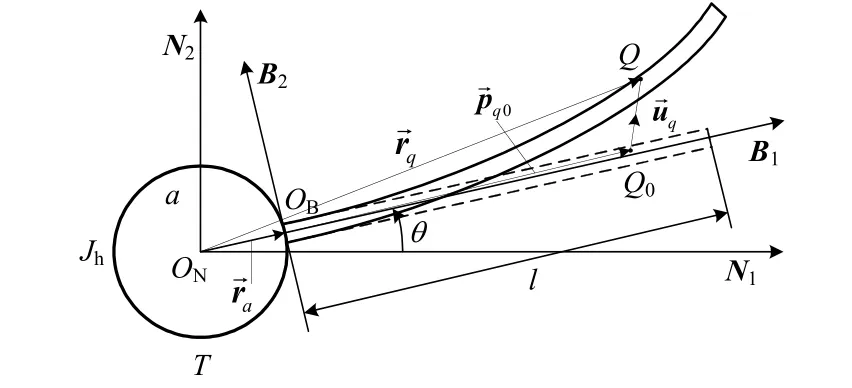
图1 刚柔耦合系统动力学模型Fig. 1 Dynamic model of rigid-flexible coupling system
图1中,中心刚体的半径和转动惯量分别为a和Jh;T为作用在其上的力矩;E、A、l、ρ分别为柔性梁的弹性模量、截面积、自然长度和体积密度;分别为惯性坐标系和固结在未变形柔性梁中与之间的夹角;为关于的矢量;未变形梁上任意点Q0变形后为Q,为其变形矢量;

1.1 梁变形描述
图2中φ为梁变形后中轴面转过的角度,柔性梁中轴线上任意点P0变形后为P,那么其变形矢量在浮动坐标系下的表示为[4-5]

式中:us、v分别为柔性梁轴向拉伸量和横向弯曲挠度;为梁变形位移的二次耦合项,是梁横向弯曲引起的纵向位移。传统零次混合坐标建模方法中,并没有考虑变形耦合,但当其与大范围运动相耦合时,将影响系统的动力学性质。矢量在浮动坐标系下的表示分别为

由图2中梁的几何变形关系,同时考虑到梁小变形下 φ为小值的假设,可以得到梁上任意点Q0(x,y)的变形矢量在浮动坐标系下的表示为

其中纵向位移 -y∂ v /∂x 项是由梁横向弯曲引起轴向伸缩变形造成的。考虑在很多实际情况下,轴向拉伸量us为微小量,忽略us得到梁上任意点的变形描述为

由公式(1)、(3)、(4)、(6)得到柔性梁上任意点Q在惯性坐标系下的速度表示

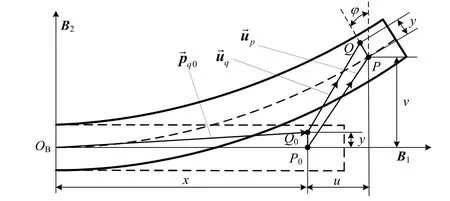
图2 梁上任意点变形描述Fig. 2 Deformation at any point on a flexible beam
1.2 系统动能
系统动能Tsys由中心刚体动能和柔性梁的动能两个部分组成,即

假设梁为细长梁,其截面惯性矩为小量,忽略梁截面转动引起的动能,可以得到的系统动能表达式为

1.3 系统势能
梁的变形梯度J和拉格朗日应变张量ε[11]分别为
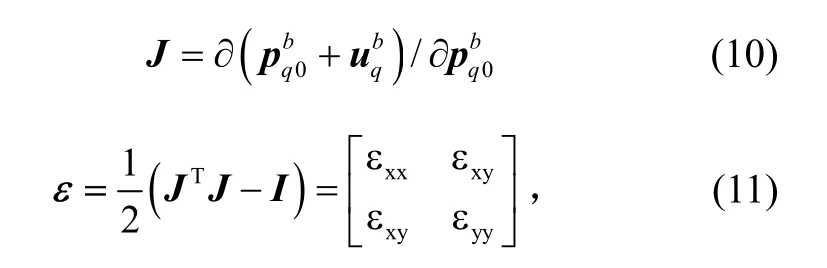
其中I为单位阵。将式(4)、(5)、(10)代入式(11),得到柔性梁剪切应变 εxy= 0,y方向的应变εyy=0,而x方向的应变εxx≠0,可以看出应变张量ε满足Euler-Bernoulli梁的假设。考虑小变形、小应变的假设,忽略εxx中高阶项,则得

系统的势能只考虑梁的应变能,那么正交各向同性材料构成的等截面柔性梁的势能为

1.4 连续动力学模型
利用Hamilton最小作用原理来建立系统的动力学方程为
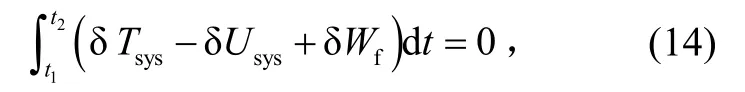
式中:δUsys为系统势能变分;δTsys为系统动能变分;δWf=Tδθ为外力做功变分。
将式(9)、(13)代入方程(14),省略一些关于uf的高阶小量,得到刚柔耦合系统的一次近似动力学方程

及边界条件

1.5 离散动力学模型
为便于动力学仿真和控制器设计,须对偏微分方程(15)、(16)进行离散化;同时为避免假设模态法在模态选择上的随意性影响动力学模型的精度,采用有限元 Galerkin加权残值法[12]对刚柔耦合动力学方程组(15)、(16)进行离散化。
如图3所示,将总长为l的柔性梁等分为n个长度le=l/n的两节点单元段,得n+1个节点,第一个节点位于浮动坐标系原点OB。Li=l(i-1)/n为第i节点距离浮动坐标系原点OB的距离,为梁上中线点在第i单元段内的纵向坐标,
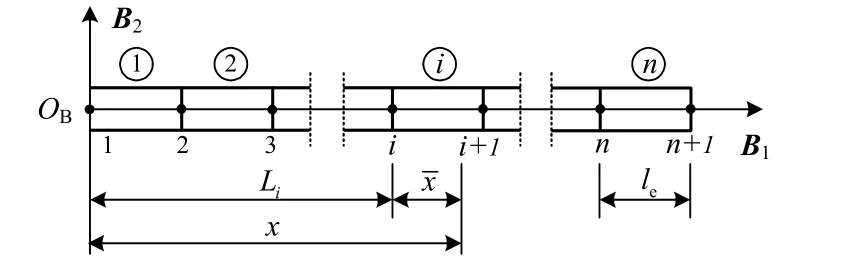
图3 柔性梁有限元模型Fig. 3 Finite element model of flexible beam

式中:vi( t)为第i节点在浮动坐标系内的横向平移量;定义梁的单元形函数[11]

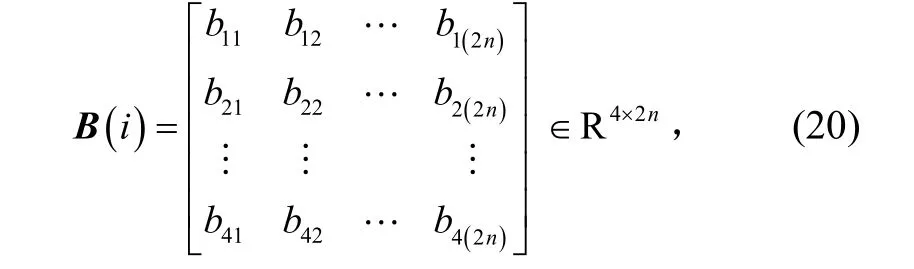
方程组(15)、(16)的有限元离散化模型为
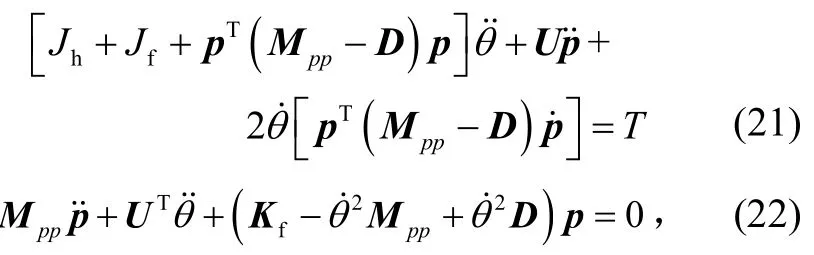
其中的常值量表示如下:
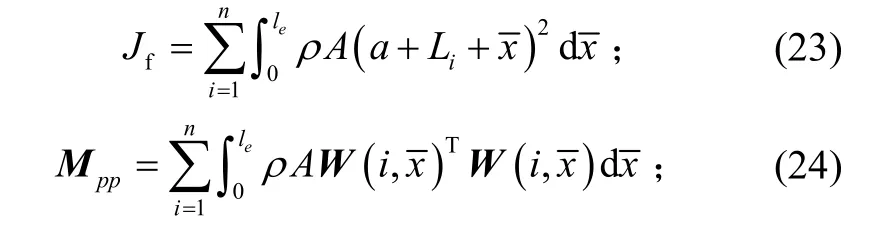

2 数值仿真
为验证本文精简的动力学模型是否能正确预示系统的动力学行为且有足够的精确性,并适合控制器设计,取两组动力学模型进行仿真对比分析。这两组模型分别为:模型 1——文献[4]中实验验证的动力学模型,并忽略其末端质量块的影响;模型2——本文动力学方程(21)、(22)。取系统物理参数:柔性梁的长度l = 8 m,杨氏弹性模量为E = 6.895 2×1010N/m2,体积密度ρ =2.766 7× 103kg/m3,截面积 A=7.3×10-5m2,截面惯性矩I =8.2×10-9m4,中心刚体半径a = 1 m,转动惯量
2.1 动力刚化分析
梁从静止开始加速旋转,采用文献[8]介绍的旋转规律,在时间 t =15 s内达到角速度θ˙= 4 rad/s,即

图4所示为模型1梁端点轴向拉伸量。当角速度达到4 rad/s时,8 m梁的端点轴向拉伸量仅为1.301×10-4m左右,并有微幅振动。图5所示为两模型梁末端的横向位移对比图,两模型梁末端横向位移之差随时间变化可见图6。模型2与模型1出现了动力刚化现象,梁的横向振动并没有像零次模型一样发散。模型2与模型1的横向变形位移基本一致,当角速度在 15 s后稳定在4 rad/s时,两模型的梁端点横向位移做等幅振荡,且在振动幅值和相位上只存在微小的差别。由图6可以看出最大误差在2×10-5m内,由于存在振动微小相位差,横向位移之差的幅值呈振荡形式。

图4 模型1梁端点轴向拉伸量Fig. 4 Axial tip displacements for model 1

图5 梁末端横向位移Fig. 5 Transverse tip displacements
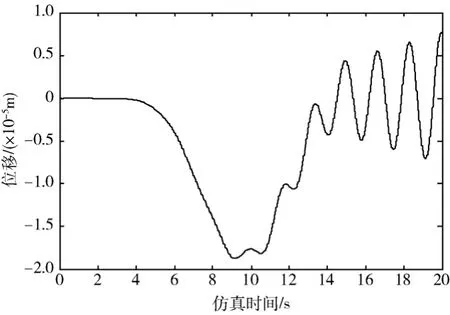
图6 两模型梁末端横向位移之间的差值Fig. 6 The difference of transverse tip displacements between model 1 and model 2
2.2 刚柔耦合分析
对模型1、2实施bang-off-bang的大角度机动控制如下,T为控制力矩,

图7所示为模型1梁端点轴向拉伸量曲线。在整个控制过程中模型1梁端点轴向拉伸量非常微小,最大约9×10-7m,完全可以忽略。图8所示为模型1和模型2的刚体角度曲线,图9为两模型刚体角度之间的差值曲线。在bang-off-bang控制力矩作用下,系统在15 s时完成了3 rad左右的大角度机动,模型 1、2中刚体角度输出基本一致,只存在细微的差别。图10为在bang-offbang控制下,模型1、2中梁末端横向位移曲线,图 11为两模型末端横向位移之间的差值曲线。可以看出:在方波的激励下,15 s控制结束时,梁端点发生了幅值达0.15 m左右的横向振动,模型1、2中梁末端横向位移输出基本一致,差别微小。

图 7 模型1梁端点轴向拉伸量Fig. 7 Axial tip displacements for model 1

图 8 刚体角度Fig. 8 Angular displacement of the hub

图 9 两模型刚体角度输出之间的差值Fig. 9 Difference of angular displacements for the hub between model 1 and model 2
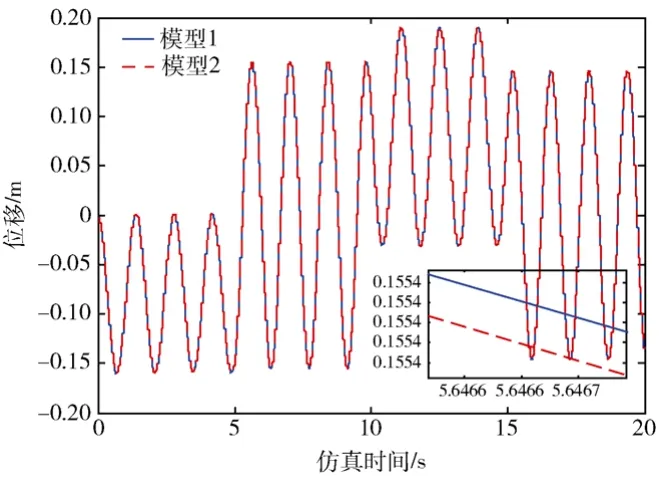
图10 梁末端横向位移Fig. 10 Transverse tip displacements
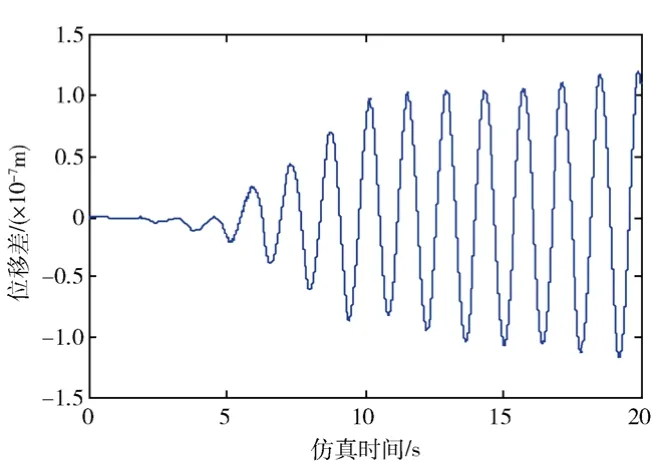
图11 两模型梁末端横向位移之间的差值Fig. 11 The difference of transverse tip displacements between model 1 and model 2
所以,忽略轴向拉伸量的模型2与实验验证的动力学模型1相比,也正确地预示了刚柔耦合系统的动力学特性,在梁的横向振动以及中心刚体运动输出上达到了同一级别的精度,完全满足控制器设计高精度的要求;同时,由于轴向拉伸量的忽略降低了系统状态变量并减少了动力学方程中的强非线性项,更利于控制器的设计。
3 结论
1)在柔性梁经历大范围运动时,梁轴向拉伸量对梁横向振动的固有频率的影响很小。
2)忽略轴向拉伸量的动力学模型 2与实验验证的动力学模型1相比,正确地预示了刚柔耦合系统的动力学特性。
3)在变形位移场描述中计及纵向变形的二次耦合项,同时忽略轴向拉伸量,可以减少动力学方程中的强非线性项及状态变量,达到简化动力学模型的目的。
4)本文模型是一种能够用于实际控制系统设计的高效、高精度的一次近似刚柔耦合动力学模型。
(
)
[1] Hu Qinglei, Shi Peng, Gao Huijun. Adaptive variable structure and commanding shaped vibration control of flexible spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 804-815
[2] Shan Jinjun, Liu Hongtao, Sun Dong. Modified input shaping for a rotating single-link flexible manipulator[J]. Journal of Sound and Vibration, 2005, 285(1-2): 187-207
[3] Kane T R, Ryan R R, Banerjee A K. Dynamics of a cantilever beam attached to a moving base[J]. Journal of Guidance, Control, and Dynamics, 1987, 10(2): 139-151
[4] 杨辉, 洪嘉振, 余征跃. 一类刚-柔耦合系统的模态特性与实验研究[J]. 宇航学报, 2002, 23(2): 67-72
Yang Hui, Hong Jiazhen, Yu Zhengyue. Vibration analysis and experiment investigation for a typical rigid-flexible coupling system[J]. Journal of Astronautics, 2002, 23(2): 67-72
[5] Sharf I. Geometric stiffening in multibody dynamics formulations[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(4): 882-891
[6] Mayo J M, Garcia-ballejo D, Dominguez J. Study of the geometric stiffening effect: comparison of different formulations[J]. Multibody System Dynamics, 2004, 11(4): 321-341
[7] 杨辉, 洪嘉振, 余征跃. 动力刚化问题的实验研究[J].力学学报, 2004, 36(1): 118-124
Yang Hui, Hong Jiazhen, Yu Zhengyue. Experimental investigation on dynamic stiffening phenomenon[J]. Acta Mechanica Sinica, 2004, 36(1): 118-124
[8] 蒋建平, 李东旭. 带太阳帆板航天器刚柔耦合动力学研究[J]. 航空学报, 2006, 27(3): 418-422
Jiang Jianping, Li Dongxu. Research on rigid-flexible coupling dynamics of spacecraft with solar panel[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(3): 418-422
[9] Cai G P, Lim C W. Dynamics studies of a flexible hubbeam system with significant damping effect[J]. Journal of Sound and Vibration, 2008, 318(1-2): 1-17
[10] Deng Fengyan, He Xingsuo, Liang Li, et al. Dynamics modeling for a rigid-flexible coupling system with nonlinear deformation field[J]. Multibody System Dynamics, 2007, 18(4): 559-578
[11] Shabana A A. Dynamics of multibody systems[M]. 3rd ed. New York: Cambridge University Press, 2005: 164-166
[12] Zienkiewicz O C, Taylor R L. The finite element method (Volume 1: The Basis)[M]. 5th ed. Oxford: Butterworth-Heinemann, 2000: 39-52

