无向哈密顿图的自适应遗传算法*

侯爱民 郝志峰 陈小莉 沈丹华

(1.华南理工大学计算机科学与工程学院,广东广州 510006;2.广东工业大学计算机学院,广东广州 510090;3.东莞理工学院计算机学院,广东东莞 523808)

无向哈密顿圈的判定问题是一个 NP完全问题.到目前为止,任何一个 NP完全问题都还没有找到一个多项式时间复杂度的判定算法.因此,文中试图寻找效率更佳的近似算法,用于判定哈密顿圈问题.

在经典的无向哈密顿圈的判定算法中,回溯算法存在路径选择的全排列组合[1],其最坏时间复杂度为指数阶.路径集算法使用剪枝技术,进行不带回溯操作的深度优先搜索[2].剪枝技术能否保证算法收敛,有待于进一步证明.通路矩阵算法的矩阵乘法运算是多项式时间复杂度的[3],但通路矩阵的元素(路径集合)是n!数量级的(n为顶点个数).逐点循环递归算法使用带回溯操作的深度优先搜索法来求解所有哈密顿圈[4],其最坏时间复杂度为指数阶.

近年来出现的一些智能算法,可对路径选择的全排列组合进行一定的筛选.如遗传算法使用继承法从n个顶点的完全图 Kn的所有哈密顿圈递归推出Kn+1的所有哈密顿圈,使用选择法从Kn+1的所有哈密顿圈中删除实际上不存在的哈密顿圈[5],但 n个顶点的完全图Kn共有(n-1)!/2个哈密顿圈. DNA算法使用碱基(T、C、A、G)对图的顶点和边进行 DNA分子编码[6],每条边甚至会有 3×1013个副本,DNA溶液用量是图的规模(顶点和边的数目)和所要解决问题的指数函数,因此,该方法用于解决较大规模(如具有40个顶点)的哈密顿圈问题是不现实的.Hopfield神经网络算法使用边赋权的圆内接正n边形将哈密顿圈问题转换成旅行商问题,定义最小偏差率,采用动态消元法降低实际偏差率,但运行状态与最大迭代次数、运行次数、种子数密切相关,仅对 30个顶点以内的简单图进行了实验[7].

文献[8-9]中对简单连通无向图 G使用充分条件“连通度κ(G)≥独立数α(G)”来求解哈密顿圈,虽然基本圈扩展操作是多项式时间复杂度的,但对于不满足充分条件的哈密顿图,该算法有可能找不到哈密顿圈,即存在路径选择的不确定性.如果想对所有的不满足充分条件的哈密顿图都有效,则必须进行回溯操作.文献[10]中使用路径扩展法求解随机图的哈密顿圈.在此基础上,文献[11-12]中对旋转操作进行了改进,时间复杂度分别为 O(n4+ε)和O(n3lgn),ε＞0.但这些算法存在如下不足:随机图的判定算法都是概率上的“几乎总是”的“好”算法,但总有一些具体图,使得这类算法失效.对于边数超过3nlgn的最大非哈密顿图的判定,这类算法往往失效.对于最小顶点度数为 k的最大非哈密顿图共有条边.由于旋转操作的次数有一个阈值,当超过该阈值而强行停止算法时,有可能还没有得到正确的结果.如果不设置阈值,则退化成完全回溯法.特殊图的哈密顿圈算法存在多项式时间复杂度[13-15],但不能处理一般图,甚至不能处理平面图.随机图的哈密顿圈算法和特殊图的哈密顿圈算法都是采用扩展和旋转技术,对路径选择/基本圈选择的全排列组合进行启发式筛选.

受文献[8,16]中无向哈密顿图的必要条件的启发,文中将“面”的视角换成原子圈的视角,对哈密顿图的特征进行研究,在提出基本圈的分解、合并、连通,以及原子圈(即不可分解的基本圈)和公共边连通等概念的基础上,提出了一个新的无向哈密顿图的充分必要条件.根据这个充分必要条件,使用基本圈作为染色体,设计了一个具有自适应特征的、融合了哈密顿圈领域知识的混合遗传算法.自适应主要表现在染色体是一种可拼接和可分解的编码方案.混合方式是在繁殖(交叉、变异)算子构造中融入了哈密顿圈是由一些具有单条公共边连通特性的原子圈进行合并而成的专门领域知识.文中算法在搜索哈密顿圈的过程中,会朝着生成哈密顿圈或最大长度基本圈的方向前进.对于哈密顿图,经过若干代进化后,收敛于某一个哈密顿圈上;对于非哈密顿图,经过若干代进化后,遗传操作无法再继续执行,进化现象不再发生,收敛于某一个最大长度的基本圈.最后通过实例测试了文中算法的效果.

1 无向哈密顿图的充分必要条件

定义1 给定简单连通无向图G=(V,E),V为图G的顶点集合,E为图G的边集合.基本圈C的一个分解是指图G中一条边e=(u,v)将长度为r的基本圈C分割成长度为s和t的两个基本圈C1和C2.其中r+2=s+t,u,v∈V(C),V(C)=V(C1)∪V(C2),E(C)∪e=E(C1)∪E(C2).

定义2 给定简单连通无向图G=(V,E),V为图G的顶点集合,E为图G的边集合.两个基本圈C1和 C2的一个合并是指由 C1和 C2的所有顶点构成图G中的一个基本圈C.其中V(C)=V(C1)∪V(C2),E(C)=E(C1)E(C2)=E(C1)∪E(C2)-E(C1)∩E(C2).

定义3 给定简单连通无向图G=(V,E),V为图G的顶点集合,E为图G的边集合.如果对任意的u∈V(C1)和v∈V(C2),都存在一条从u到v的路径,则两个基本圈C1和C2是连通的.

定义4 给定简单连通无向图G=(V,E),V为图G的顶点集合,E为图G的边集合.对于两个基本圈C1和C2,如果存在一条边e∈E(G),使得e∈E(C1)且e∈(E(C2),则称边e是基本圈C1和C2的公共边,C1和C2以公共边e连通.

定义5 给定简单连通无向图G=(V,E),V为图G的顶点集合,E为图G的边集合.不能分解成更小长度基本圈的基本圈,称为原子圈.

定理1 在简单连通无向图中,一个基本圈要么是原子圈,要么总是可以分解成若干个原子圈,这些原子圈按照某种次序以单条公共边连通.

定理2 在简单连通无向图中,一个基本圈要么是原子圈,要么总是可以由若干个原子圈合并而成,这些原子圈按照某种次序以单条公共边连通.

推论1 给定简单连通无向图G=(V,E),V为图G的顶点集合,E为图G的边集合为图G的顶点个数),δ(G)≥2(δ(G)为图G的最小顶点度数).图G是哈密顿图,当且仅当哈密顿圈要么是一个包含所有顶点的原子圈,要么总是可以分解成若干个原子圈,或者说,总是可以由若干个原子圈进行合并而成,这些原子圈按照某种次序以单条公共边连通.

2 自适应遗传算法

基于无向哈密顿图的充分必要条件,文中提出一种自适应遗传算法,用于求解无向哈密顿圈问题.由于染色体是原子圈或基本圈,任意选择的两个染色体不一定能结合成新的染色体.只有符合交叉/变异运算的前提条件的两个染色体才能结合成新的染色体.所以,染色体编码就具有可拼接、可分解的特点,算法具有自适应、利用专门领域知识的特点.

2.1 可拼接/可分解的染色体编码

定义6[17]如果A=a1a2…aL是一个L码,B= b1b2…bM是一个M码,则A∨B=a1a2…aLb1b2…bM称为A与B的一个拼接.对应地,A、B称为D(D= A∨B)的一个分解.

定义 7[17]一个编码 d称为可拼接的,如果任意L码A和M码B的拼接A∨B仍是满足相同特性的L+M码.一个编码d称为可分解的,如果任何N码D可分解表示为D=A∨B,其中A为L码,B为M码,L和M是满足L+M=N的任何正整数,且D的解码在下述意义下是可分解的:存在常数a、b、c,使得

其中d-1(*)表示*的解码.

文献[17]的研究结果表明,一个可拼接/可分解的编码通常构成遗传算法自适应实现的基础.它为用“小算法”求解“大问题”提供框架.

2.2 自适应遗传算法的设计

选择基本圈作为染色体的编码.染色体中基因座的码值取自顶点编号.基本圈的顶点个数作为该染色体的适应度度量.初始种群由原子圈构成,第一代及之后的种群由原子圈和基本圈混合构成.根据适应度比例选择任意两个染色体进行配对,按交叉概率执行交叉操作.为保证交叉运算后获得的染色体仍是一个基本圈,要求参加交叉运算的两个染色体满足以单条公共边连通的条件.具体的交叉运算就是将两个染色体拼接成一个更大的染色体.如果两个染色体仅有两个顶点编号相同,且这两个编号在一个染色体中是相邻的,在另一个染色体中是不相邻的,那么,通过对不相邻的那个染色体重新排列顶点编号,有可能使变异后的染色体与原来相邻的染色体组成一个满足以单条公共边连通的染色体对.当然,重排顶点编号后,要保证染色体仍是一个基本圈.具体的变异运算就是将一个染色体的顶点编号重新排列.终止进化准则如下:若存在一个长度为n的染色体,则终止进化;若不再有更长的新染色体产生,则终止进化;若不再有新染色体产生,则终止进化.

2.3 初始种群的生成

初始种群的生成步骤如下:

(1)从某个顶点出发,采用不带回溯操作的深度优先遍历方法,在其遍历路径上寻找所有基本圈.

(2)依次以其它顶点为出发点,重复第(1)步的过程.

(3)如果不存在任何基本圈,则该图是树或森林,算法停止;如果存在长度为n的基本圈,则该圈就是一个哈密顿圈,算法停止;如果以每个顶点作为出发点的遍历路径上访问的顶点个数不为 n,则该图是不连通图,算法停止.

(4)在已经找到的基本圈集合中,最小长度的基本圈是原子圈.依次用已知的原子圈过滤其它基本圈,剩下来的基本圈都是原子圈.

3 自适应遗传算法的性能分析

3.1 种群序列{X(t)}的收敛性

文献[17]中使用概率分析法,讨论了遗传算法的收敛性.对于哈密顿图,根据推论 1,必有一个哈密顿圈存在,所以由哈密顿圈作为元素组成的最优解集合F*满足F*≠ .随着进化代数的增加(即t→∞),必然有种群X(t)中包含哈密顿圈,即X(t)∩ F*≠ ,所以成立,即种群序列{X(t)}依概率弱收敛到F*.

3.2 初始种群的有效性

文中采用不完全法,即不带回溯的深度优先遍历方法寻找基本圈和过滤基本圈方法生成原子圈,来生成初始种群,因此不能生成所有的原子圈,自适应遗传算法的收敛性取决于生成的初始种群的有效性.通过对原子圈包含的每条边的分布规律进行分析,不难发现:每条边至少在 3个不同的原子圈中出现,每个顶点至少在 3个不同的原子圈中出现;原子圈包含边的分布规律较为随机、均匀,原子圈包含顶点的分布规律也较为随机、均匀;最小长度的原子圈及其它长度较小的原子圈,数量众多,被遗漏的较少,且它们覆盖了所有的顶点;基于初始种群进化生成的新种群有很大的变化,且包含的边的分布规律较为随机、均匀.因此,采用不完全法生成初始种群,仍然有很大机会概率保证初始种群的有效性,从而保证自适应遗传算法的收敛性.

4 实验及结果分析

使用C语言编程实现文中所提出的自适应遗传算法,对一些典型图形以及树、不连通图、顶点数为 100以内的随机生成图进行程序判定.所有实验均在AMD Athlon(tm)64×2 Dual Core Processor 3600Hz/1GB内存的计算机上进行,结果见表1、2.

文献[7]中提供了使用Hopfield神经网络求解10个城市的旅行商问题的运算结果,实际迭代次数取决于图的形状和环境参数的初始状态,其变化范围为 16～505.其中设定的运行次数m=200,函数srand的种子数seed=8.

从表 1中可知,文中算法的时间开销与初始种群的大小及图形拓扑结构密切相关,对于边数或面数比较多的图形(如Tutte图、Grinberg图),时间开销增长过快.根据表 2,跟踪每一代的进化结果,可以发现Tutte图在第7代时就已经找到最大圈,实验中发现Grinberg图也存在类似现象.因此,文中算法的进化代数还可以进一步减少.和Hopfield神经网络方法[7],以及染色体编码采用固定长度为 n、由全部顶点编号组成一个字符串的遗传算法等相比,文中算法的进化代数明显减少,遗传算法的自适应性能得到充分体现.

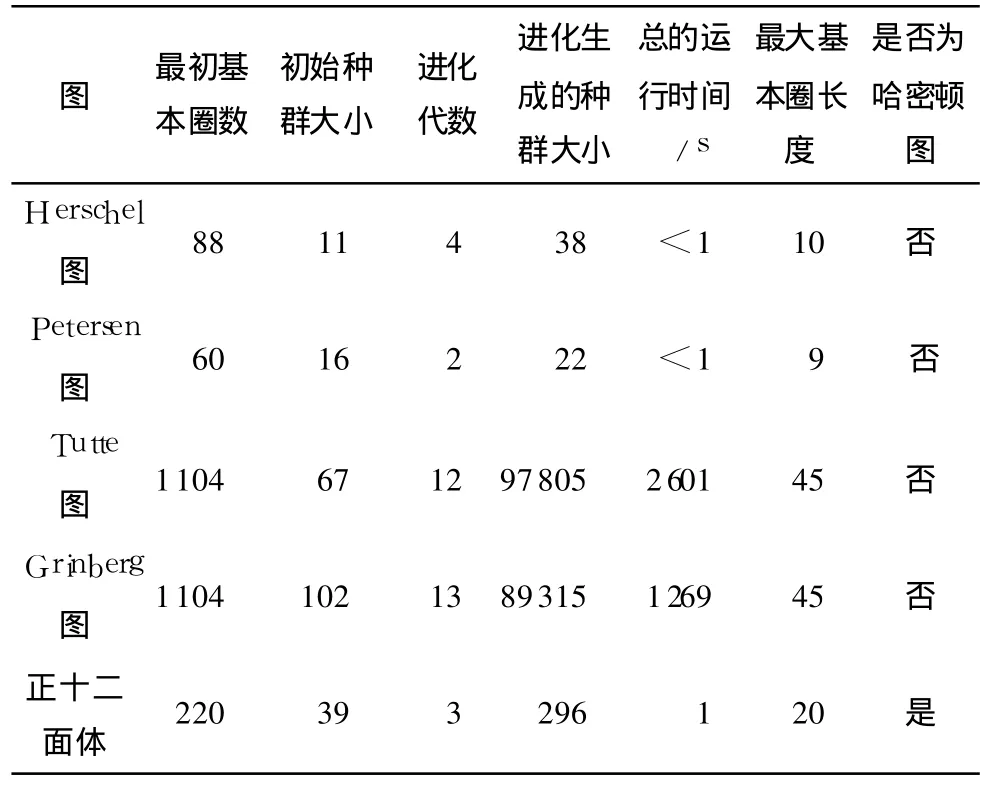
表1 在几种典型实例上自适应遗传算法的总体性能Table 1 General properties of adaptive genetic algorithm running on some typical cases

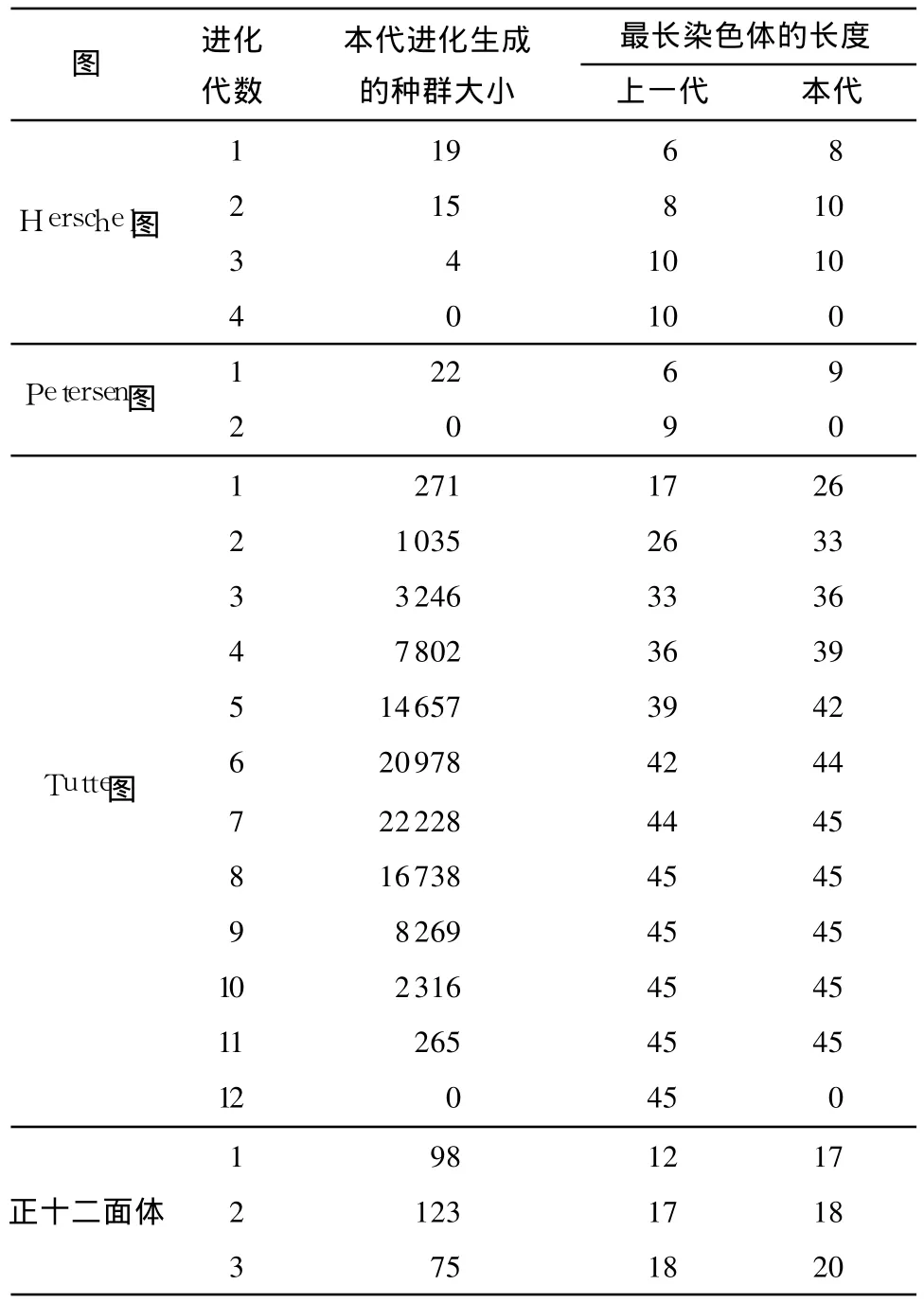
表2 在几种典型实例上自适应遗传算法的进化性能Table 2 Evolutionary properties of adaptive genetic algorithm running on some special cases

5 结语

无向哈密顿圈的判定问题至今还没有找到一个多项式时间复杂度的判定算法.为此,文中提出一种效率更佳的近似算法,用于判定哈密顿圈问题.算法由初始种群生成算法和特殊染色体编码的遗传算法组成.由于染色体是一种可拼接和可分解的编码方案,只有符合交叉/变异运算的前提条件的两个染色体才能结合成新的染色体,故遗传算法具有自适应的特点.适应度度量采用基本圈的顶点个数,从而引导遗传算法朝着最大基本圈的方向前进.实验结果表明,文中算法具有良好的求解性能.

[1] 王晓东.计算机算法设计与分析 [M].北京:电子工业出版社,2001:185-189.

[2] 姜新文.求解哈密顿图判定问题的一个新算法 [J].计算技术与自动化,1997,16(1):1-3.

Jiang Xin-wen.A new algorithm for solving the Hamiltonian graph p roblem[J].Computing Technology and Automation,1997,16(1):1-3.

[3] 郭俊杰,伊崇信,毕双艳,等.哈密顿回路存在性判定及输出算法[J].吉林大学自然科学学报,1998(2): 5-8.

Guo Jun-jie,YiChong-xin,BiShuang-yan,et al.Existence judgement and output algorithm of the Ham iltonian circuit [J].Acta Scientiarum Naturalium Universitatis Jilinensis, 1982(2):5-8.

[4] 王彦棋.逐点循环递归法求哈密顿回路 [J].哈尔滨工业大学学报,2004,36(1):115-117,121.

Wang Yan-qi.Algorithm of cycle and recursion by every vertex for getting Hamilton cycle[J].Journal of Harbin Institute of Technology,2004,36(1):115-117,121.

[5] 王彦棋.用“遗传”算法求任意图的所有哈密顿回路[J].哈尔滨工业大学学报,2004,36(12):1690-1692.

Wang Yan-qi.A genetic algorithm for getting all Hamilton cycles of any graph[J].Journal of Harbin Institute of Technology,2004,36(12):1690-1692.

[6] 洪龙,朱梧贾.Hamilton圈问题的DNA算法[J].南京航空航天大学学报,2006,38(2):222-226.

Hong Long,Zhu Wu-jia.DNA algorithm for solution to Ham ilton cycle problem[J].Journal of Nanjing University of Aeronautics and Astronautics,2006,38(2):222-226.

[7] 陆生勋.用Hop field神经网络解哈密顿回路问题[J].浙江大学学报:理学版,2010,37(2):180-184.

Lu Sheng-xun.Solving Hamilton cycle prob lem by using Hop field neural network[J].Journal of Zhejiang University:Science Edition,2010,37(2):180-184.

[8] West Douglas B.图论导引[M].李建中,骆吉洲,译.北京:机械工业出版社,2006:229-235.

[9] Chvátal V,Erdös Paul.A note on Ham iltonian circuits [J].Discrete Mathematics,1972,2(2):111-113.

[10] Pósa Louis.Hamiltonian circuits in random graphs[J]. Discrete Mathematics,1976,14(4):359-364.

[11] Bollobás B,Fenner T I,Frieze Alan M.An algorithm for finding Hamilton cycles in random graphs[C]∥Proceedings of ACM Symposium on Theory of Computing. New York:ACM,1985:430-439.

[12] Frieze Alan M.Finding Hamilton cycles in sparse random graphs[J].Journal of Combinatorial Theory:Series B,1988,44(2):230-250.

[13] Johnson JRobert.Long cycles in themiddle two layers of the discrete cube[J].Journal of Combinatorial Theory: Series A,2004,105(2):255-271.

[14] Shields Ian,Shields Brendan J,Savage Carla D.An update on them idd le levels problem[J].Discrete Mathematics,2009,309(17):5271-5277.

[15] Shields Ian,Savage Carla D.A note on Ham ilton cycles in Kneser graphs[J].Bu lletin of the Institute for Combinatorics and Its App lications,2004,40:13-22.

[16] Grinberg E J.Plane homogeneous graphs of degree three without Ham iltonian circuits[J].Latvian Mathematics Yearbook,1968,5:51-58.

[17] 徐宗本,张讲社,郑亚林.计算智能中的仿生学:理论与算法[M].北京:科学出版社,2004:13-14,67-69.