R o b o c u p 3 D仿人机器人中基于频率加权的Z M P补偿算法

李娟娟

（南京邮电大学自动化学院，南京，210003）

0 引言

研制与人类外观特征类似，具有人类智能，灵活性，并能够与人交流，不断适应环境的仿人机器人一直是人类的梦想之一。在仿人机器人的研究过程中，机器人的稳定性尤其是步态稳定性的研究已成为新一代机器人的研究重点。仿人机器人系统本身的高度非线性及运动过程中存在大量的随机干扰和各种时变的外力的作用，使得常规控制方法在实现高精确度运动控制时显得力不从心。众所周知，ZMP(Zero Moment Point)即零力矩点是机器人稳定性的一个重要评价标准，只有当ZMP位于支撑多边形内部时，仿人机器人才能保持稳定。本文就是基于该理论，在Tomoya Sato等人的补偿算法的基础上，提出了一种新的ZMP补偿控制方法，使得仿人机器人在整个步行过程中保持ZMP位于支撑多边形之内。

目前，比较成熟的基于ZMP的步态稳定性控制方法包括通过踝关节力矩进行控制、通过质心加速度控制ZMP[1,6,8]以及通过腿的摆动进行控制等等[1,8]。对于踝关节力矩控制方法而言，机器人的踝关节力矩可能会与实际值之间存在很大误差，而控制腿的摆动这种方法只适用于单足支撑的阶段。相反，通过质心加速度控制ZMP的方法[8]却可以适用于整个步行阶段[5]。另外，Tomoya Sato等人已经证实当ZMP的误差为常量或者是变化很慢时，位置补偿可以起到很好的补偿效果，使得机器人保持稳定；当ZMP的误差变化很快时，位置补偿的作用不再有效，而加速度补偿的效果明显，使机器人保持稳定。因此Tomoya Sato等人利用低通滤波器将ZMP误差分为高频分量和低频分量，对于高低频分量分别做加速度补偿和位置补偿[5,7]。本文就是在以上补偿方法的基础上，考虑到机器人的运动是一个连续的时变系统，因此ZMP误差也是高低频混杂非常严重的，要通过截止频率有限的低通滤波器将ZMP误差按照高低频明显的区分是无法实现的。因此本文提出一种新的分配方法，通过FFT[3]将ZMP误差的频率信息提取出来，将对机器人的补偿量利用加速度补偿和位置补偿的权值和来表述，其中权值的大小随着ZMP误差频率的变化不断变化。

在本文中，机器人的稳定行走是通过调整ZMP，使其尽量接近期望的ZMP值来实现的。如果ZMP可以调整到期望的ZMP值，那么就可以使机器人保持稳定，从而避免机器人摔倒。ZMP的误差是由ZMP干扰造成的，因此有必要对ZMP干扰进行预测。本文中的ZMP干扰预测器首先对ZMP的值进行预测，再根据频率的不同进行划分，从而对机器人进行位置补偿和加速度补偿。

1 Robocup3D机器人模型

本文中运用的机器人是Robocup3D仿真足球机器人，机器人的关节示意图如图1所示。该机器人是以法国的NAO机器人为实际模型，NAO类人机器人由法国Aldebaran机器人公司制造。它的高度约57cm，重量大概为4.5kg[4]。他全身共有22个自由度，这使其有很强的移动性能。

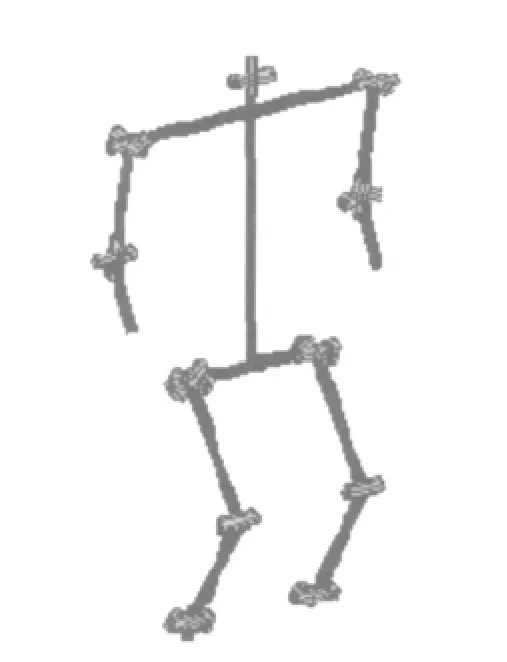
图1 机器人关节示意图

本文在研究过程中将机器人做了一定的简化，(a)假设机器人整个身体质量集中于一个点即机器人的重心；(b)假设机器人在行走过程中的高度保持不变。

2 ZMP补偿算法

假定机器人的高度是保持恒定的，其ZMP可按下式求得：

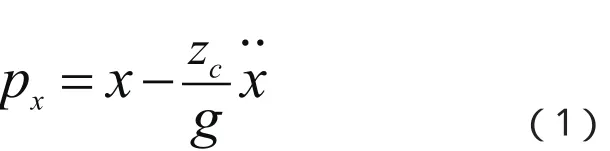
该式即ZMP方程式。式中x表示COG（机器人重心）在前进方向的坐标值；.. x表示机器人在前进方向的加速度；px表示机器人的ZMP在前进方向上的坐标值；zc表示COG的高度，在本文中我们假定是一个常量；g代表重力加速度。

ZMP的实际值与期望值之间的关系由式（2）和式（3）描述

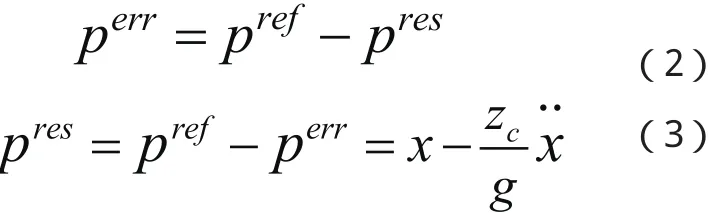
式中 perr表示ZMP的误差， pref表示ZMP的期望值， pres表示ZMP的实际值。式（3）中既有x又有因此对机器人重心轨迹的补偿可以从位置和加速度两个方面进行考虑[5]。

若只考虑通过补偿机器人的位置来实现对重心的补偿，则补偿量Δx通过式（4）和式（5）求得：

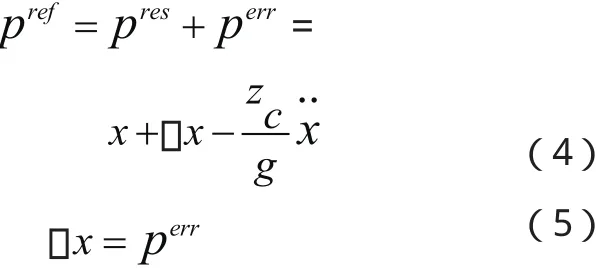
若只考虑加速度补偿，则补偿量Δx可通过式（6）和式（7）求得。

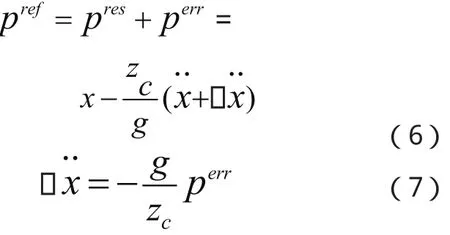
3 基于频率加权的补偿算法

位置补偿只适用于ZMP误差为常量或者变化很慢的情况下，而加速度补偿只适用于ZMP误差快速变化的情况下。然而在机器人实际行走过程中，ZMP误差的变化是不固定的，有可能在一段时间内保持不变，也有可能不断变化，而且变化频率不是固定的。因此很难确定ZMP误差在什么时候保持恒定什么时候不断变化。

针对以上这种实际情况，我们采用式（8）和式（9）求得补偿量Δx：

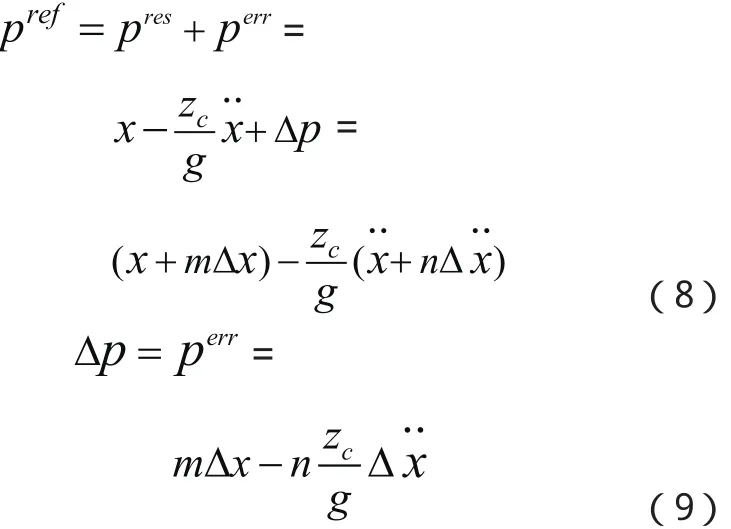
其中，m的大小与ZMP误差频率f成反比；n的大小与ZMP误差频率 f成正比。m ≤1， n ≤1并且满足m+n= 1；m表示位置补偿量表示加速度补偿量。

当ZMP误差的频率f很小时，表示ZMP的误差变化很慢，此时m的值相应的比较大，n值相应的比较小，因此在补偿过程中位置补偿占的比重大于加速度补偿的比重；相反若ZMP误差的频率 f很大时，表示ZMP的误差变化很快，此时m的值相应的变小，n值相应的变大，因此在补偿过程中加速度补偿占的比重大于位置补偿的比重。

由于本算法是根据频率的变化实时变化加权系数的大小，因此位置补偿与加速度补偿的比重在整个补偿过程中是根据频率的变化相应的变化的。在本算法中，对于高频ZMP误差和低频ZMP误差采取相同的处理方法，不存在频率分割的问题，因此不必考虑由于截止频率有限而造成的频率分配不当的误差。

4 ZMP补偿控制系统

对于ZMP实际值造成干扰的物理量称为ZMP干扰。ZMP干扰是造成ZMP误差的主要原因，因此对ZMP的干扰值进行补偿可以实现ZMP的实际值尽量接近ZMP的期望值。

Tomoya Sato等人提出的ZMP补偿控制系统是利用两个截止频率不同的低通滤波器将ZMP的误差分为高频和低频两部分，高频部分采用加速度补偿，低频部分采用位置补偿。这种方法的正确性也得到了证实，但是从准确性方面来说，由于高频和低频信号之间没有明显的界限，因此我们采用了FFT的方法获得ZMP误差信号的频率信息，根据频率的变化不断的调节补偿权值，控制位置补偿与加速度补偿的比重，从而避免了将一个高低频混合信号进行频率分割的难题。

ZMP补偿控制系统的结构如图2所示。图中 xn代表机器人重心在行走方向上的坐标， 表示扭矩的期望值，

res表示机器人的关节角度。

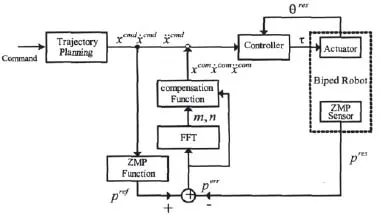
图2 ZMP补偿控制系统结构图

5 仿真测试

将上述ZMP补偿控制系统用于Robocup3D机器人上，由于在Robocup3D中的足球机器人只在一个平面即球场地面上运动，因此我们只考虑在XOY平面内的ZMP的变化。仿真过程中，用身体的位置来代替ZMP response（在XOY平面内，身体的位置近似于ZMP response的位置）。仿真结果见图3~图7。

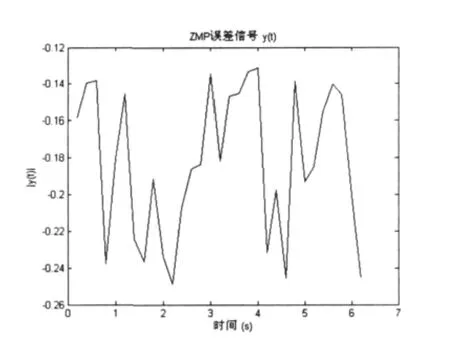
图3 原始的ZMP误差

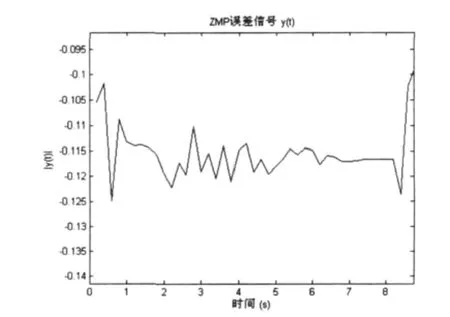
图4 加入补偿系统后的ZMP误差

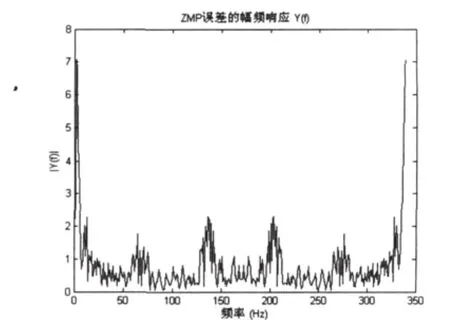
图5 ZMP原始误差的幅频响应

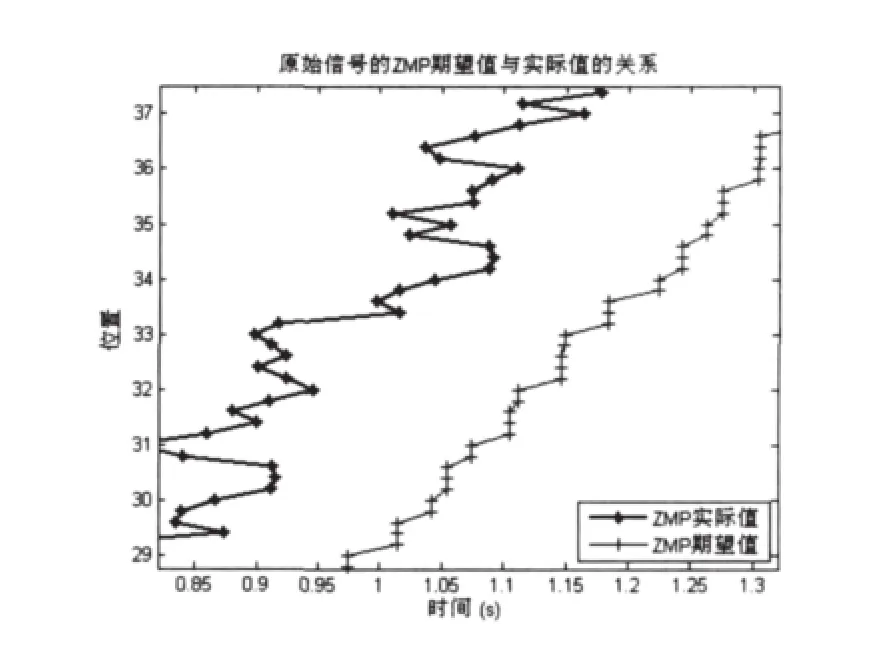
图6 原始的ZMP期望值与实际值比较

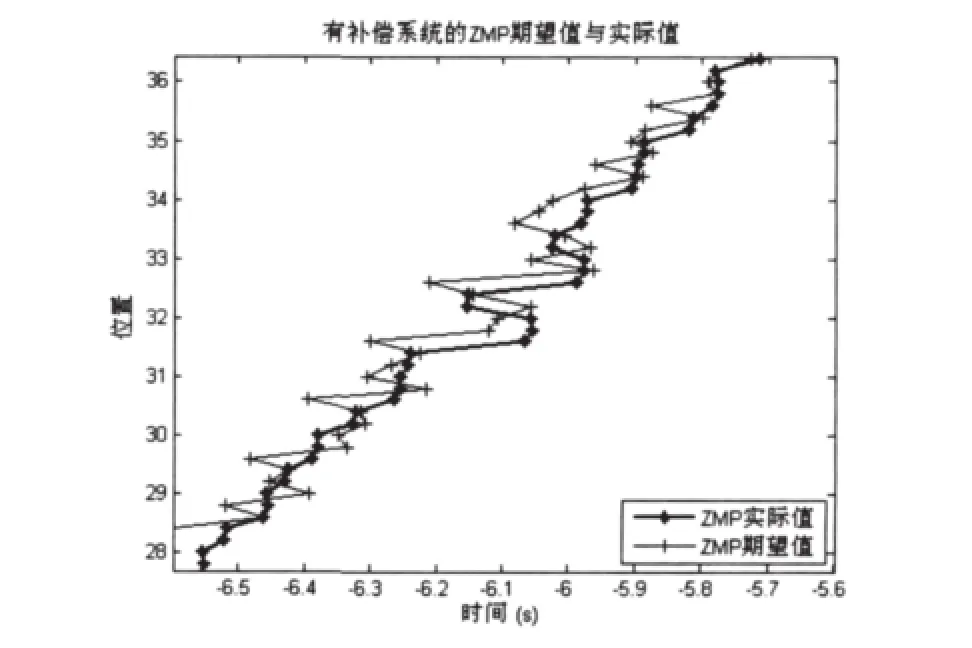
图7 加入补偿系统的ZMP期望值与实际值比较

经过比较图3与图4可以很明显的看出加了补偿系统之后，ZMP的误差明显减小，因此从误差分析的角度考虑，上述补偿系统对Robocup3D机器人的稳定性是有利的。由图5可知在步行过程中，ZMP误差的频率是不断变化的，高频低频混杂在一起，因此用截止频率有限的滤波器区分信号势必会存在一定的误差。然而在本文中采用的根据频率加权的方法，因此不必考虑因为频率混杂造成的误差。图6与图7很形象的将原始的ZMP期望值实际值的差别与加了补偿系统后的ZMP期望值实际值的差别做了比较，进一步在信号自身角度验证了该补偿系统对Robocup3D机器人稳定行走的作用。

6 结束语

由于仿人机器人的内在稳定性很差，在步行过程中易受环境的干扰，因此本文针对机器人的稳定性控制提出了一种新的补偿算法。该算法通过实时检测机器人零力矩点的误差，利用误差频率的变化对机器人的零力矩点的位置进行调整，从而实现机器人的稳定行走。

实现机器人的稳定行走是机器人完成各种其他高级动作的基础，因此也成为发展机器人事业的重中之重。本文所述的补偿算法虽然对保持机器人的稳定性有一定的作用，但仔细观察图7还是存在细微的误差，再加上本文只是在Robocup3D的仿真机器人上进行的测试，对于实体机器人的稳定性控制还有待于我们进一步的研究。

[1] 梶田秀司（日）. 仿人机器人[M]. 管贻生 译. 北京:清华大学出版社, 2007.

[2] 肖南峰 . 智能机器人[M]. 广州: 华南理工大学出版社，2008.

[3] 周辉，董正宏 . 数字信号处理及MATLAB实现[M].北京 . 中国林业出版社，2006.

[4] Robocup3D Server Develop Group. RoboCup Soccer Server 3D Manual. 2009.

[5] Tomoya Sato and Kouhei Ohnishi. ZMP Disturbance Observer for Walking Stabilization of Biped Robot[J]. In IEEE Transactions on Robotics, 2008, 290-295.

[6] T.Sugihara,Y.Nakamura and H.Inoue. Realtime Humanoid Motion Generation through ZMP Manipulation based on Inverted Pendulum Control[J]. Proceedings of the 2002 IEEE International Conference on Robotics and Automation, 2002,2(5): 1404-1409.

[7] Tomoya Sato，Sho Sakaino and Kouhei Ohnishi: Parameter Design for ZMP Disturbance Observer of Biped Robot,2008,1650-1655.

[8] Yu Okumura, Tetsuo Tawara, Ken Endo, Takayuki Furuta and Masaharu Shimizu: Realtime ZMP Compensation for Biped Walking Robot using Adaptive Inertia Force Control, 2003, 335-339.