基于二级多点逼近算法的航天器结构优化设计

陈珅艳 黄 海

(北京航空航天大学 宇航学院,北京 100191)

基于二级多点逼近算法的航天器结构优化设计

陈珅艳 黄 海

(北京航空航天大学 宇航学院,北京 100191)

在某新型卫星结构研制的初样阶段,建立了卫星初始设计的有限元模型.以主承力桁架结构中各梁的截面尺寸为设计变量,考虑整星模态频率和强度约束,建立了以结构重量最轻为目标的优化模型.应用二级多点逼近优化算法进行了结构优化计算,在每一个计算周期中,原结构优化问题先转化为具有较高精度的第 1级多点近似问题,该问题则通过可由对偶法快速求解的第 2级近似问题逼近.经过初步试算、设计改进和再优化 3个阶段,设置并进行了一系列的优化计算,逐步明确了设计的方向和各结构参数的取值范围,得到了合理的可行方案,为该卫星平台结构初样的详细设计提供了参考,同时表明所采用的优化方法适用于工程结构优化问题.

结构优化;卫星;工程;应用

航天器的尺寸、重量和复杂性不断提高,由于火箭的运载能力有限,航天器的结构重量成为一个关键的设计因素.在卫星结构研制初样阶段中,欲实现结构重量最小且同时满足多个设计约束,需首先进行反复的初样设计与初样分析,直到满足总体的设计要求.将结构优化技术应用于初样的设计与分析,可以有效提高设计效率和水平.在国外的卫星结构设计中已有不少成功案例,如美国 TRW公司在 GRO和 OMV的初样设计中应用结构优化技术,其结构质量分别减少 30%和20%[1];在波音等公司,结构优化已成为结构设计中的规定环节.我国的卫星结构设计中,优化技术也逐步得到了重视和应用,已在某些卫星的部件及整星设计中实施[2-3].由于卫星结构中涉及大量内部组件和有效载荷的装配,故应用形状优化和拓扑优化的可能性不大.目前,我国的卫星结构优化设计中以截面尺寸优化为主.然而,截面尺寸优化的应用过程中,优化问题建模的合理性、优化系统的可行性、优化算法的有效性和计算效率等仍是经常遇到的问题.

本文在某新型卫星结构研制的初样阶段,建立了卫星初始方案的有限元模型.以主承力桁架中各梁的截面尺寸为设计变量,考虑整星横向模态频率和强度约束,建立了以结构重量最轻为目标的结构优化模型.应用基于二级多点逼近优化算法[4]的结构优化系统 ESSOSII[5]进行优化计算,旨在为该卫星平台结构初样的详细设计提供参考.

1 结构优化问题描述

某卫星由主结构平台和有效载荷舱构成,设计总重为 7000 kg.为了提高结构的承载效率,其主结构拟采用梁板复合结构[6],即由梁和板共用空间、共同承受载荷的结构形式.在初样阶段的初期,应根据工程要求和工艺条件,对初始方案进行分析和优化设计,从而为主结构平台中承力梁构形的拓扑调整、截面尺寸和关键结构参数(如整星质心高度等)确定提供设计依据,同时减轻重量.整星刚度满足一阶横向和纵向频率分别不小于 11Hz和 30Hz.同时满足发射状态下,整星在准静态惯性载荷(见表 1)作用下的强度要求和稳定性要求.

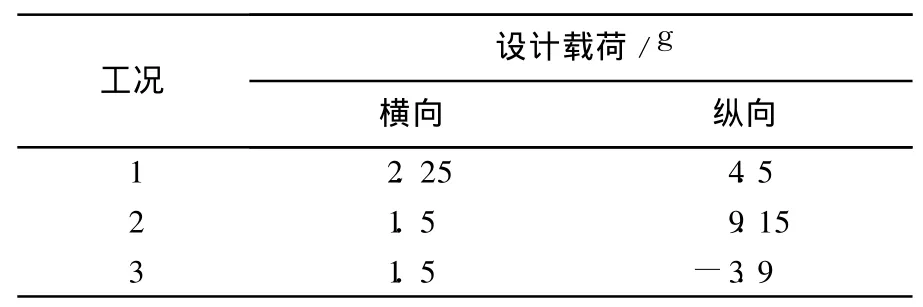
表 1 准静态惯性载荷条件

2 卫星结构有限元分析模型

根据方案阶段确定的卫星主结构的传力特点和初始设计构形,经简化后建立了结构的有限元分析模型,主要由壳、梁和杆单元构成.梁板复合结构中梁单元与壳单元边界节点重合.在结构动力学特性分析中,考虑结构平台附属结构和载荷舱中有效载荷的质量分布状况,将这些质量以非结构质量的方式施加于各相关的壳和梁杆单元上,或以集中质量点的形式用刚性连接单元RBE2固连于拟安装的部位.整星有限元模型如图 1所示,包括 24 669个节点,26844个单元,图中去掉了一块侧板.

图1 整星有限元模型

根据星箭的连接状况,模型的边界条件定为连接环底部固支.对其进行模态分析,并根据工程需求对其进行修正,使整星模态频率分布和振型合理、传力路线正确,从而可将其作为优化设计的结构分析模型.为了确定合理的整星质心高度,通过调整非结构质量的分布,得到质心高度分别为1.8m和 1.6m的两个初始模型,对应的整星第 1阶模态频率分别为 10.41Hz和 11.62Hz.

3 结构优化设计模型

该结构优化问题可表述为以下非线性数学规划问题:

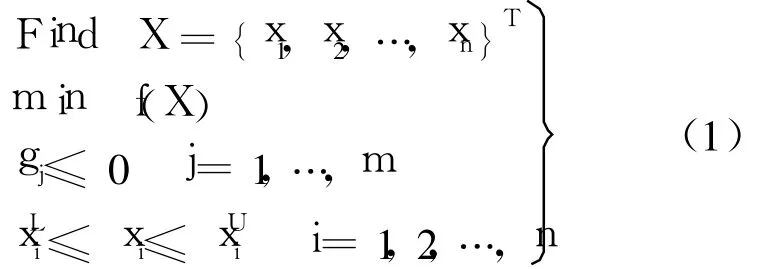
4 二级多点逼近优化算法

采用基于二级多点逼近优化算法的结构优化系统 ESSOSII对该问题进行优化前处理和寻优计算.在每一个优化迭代步中,首先进行当前结构的模态分析和 3种过载工况下的静力分析,然后对约束条件进行评估和临时删除,并计算临界约束和目标函数(结构重量)对设计变量的一阶导数.其中,结构响应和相应的导数信息由航天部门广泛使用的通用有限元程序 Nastran计算得到.

4.1 目标函数和约束条件近似

算法对原优化问题实行两级近似的求解策略.

1)第 1级多点近似函数.算法基于约束函数在多个点上的函数值及其导数,构造一种多元逼近函数,第 p个结构优化周期内,形成逼近原结构优化问题的第 1级序列显式近似问题为

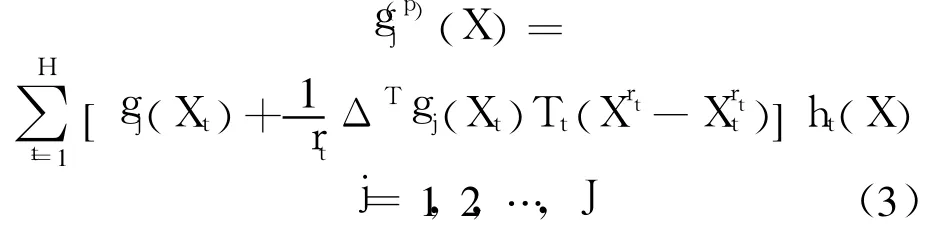
式中,Δ gj(Xt)为 gj(X)在 Xt的导数;Tt(Xt)为一个对角矩阵;ht(X)为第 t个点的影响因子;指数 rt(t=1,2,…,H)是控制函数非线性程度的自适应参数;H为构造近似函数所用的设计点数目上限(取 H=5),当已知点的数目超过 H时,只保留最后得到的 H个点.在已知设计点上,(X)的数值及 1阶导数与原函数相等.在优化初始阶段,只有一个已知设计点时,式(3)退化为1阶 Taylor展开.随着优化过程的进行,近似问题的有效范围自动增大,从而具有较高的寻优效率和适应性.

2)第 2级近似问题.第 1级近似问题(2)中约束函数的数目通常远小于设计变量数目,因此用对偶方法求解具有很高的计算效率.但对偶方法所能求解的规划问题要求对偶变量与原变量之间具有显式的函数关系,而问题(2)仍为复杂非线性,不能利用对偶方法直接求解.因此,问题(2)的目标函数和约束函数分别在设计变量空间X和它的倒变量空间进行线性泰勒展开,形成第2级序列近似问题,以逼近问题(2).

4.2 对偶法求解近似问题

第 2级近似问题的解通过求解其对偶问题获得,详细算法见文献[4].当满足第 2级近似问题的收敛精度后,获得问题(2)的解.之后,修改设计变量对应的结构参数,进行下一次全结构分析和敏度分析,转入下一个设计周期,直至达到设定的第 1级近似问题的收敛精度后停止迭代.

5 计算结果

计算过程中,第 1级近似问题和第 2级近似问题的收敛精度分别取 0.005和 0.0005.

5.1 初步试算

首先,对质心高度 H为 1.8m的整星模型进行优化.由于设计变量的初值和上下限尚不明确,需在试算的过程中给以初步确定,故梁板复合结构的内埋梁暂取薄壁圆管截面,设内径 R=0.04m不变,以壁厚 t作为设计变量.主隔板内埋梁左右对称,分为 5组(如图 2a所示),分别对应第 1～5号设计变量;次隔板内埋梁壁厚对应第 6号设计变量.第 7～11号设计变量分别为主支架圆管梁壁厚、对接环法兰宽度、储箱拉杆宽度和上下框架矩形截面梁壁厚.设计变量的初值取经验值,对上下限暂设置了较大的变化范围,以考察其变化趋势.整星基频约束 ω1分别为 11.0Hz和10.5Hz时的优化结果见表 2.可见,整星模态基频是临界约束;质心高度为 1.8m时,欲使基频达到11.0Hz将导致重量大幅增加.

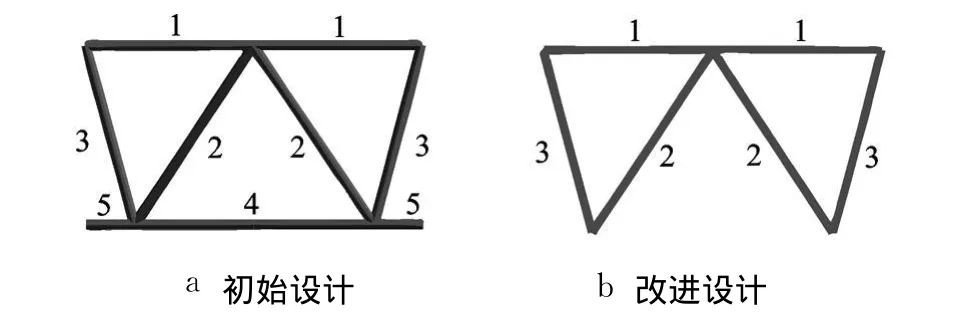
图2 主隔板内埋梁

表 2 初步试算优化结果 mm

接着,对质心高度 1.6m的整星模型进行优化.设计变量的初值和上下限不变,整星基频约束分别取 11.8Hz,11.6Hz和 11.4Hz,计算结果见表 1.可见,质心高度 1.6m时,随着模态基频下限的变化,各结构参数的变化趋势较为明显.基频下限取 11.4Hz时,6组内埋梁的壁厚中,次隔板内埋梁壁厚最大,为 2.91mm,主隔板内埋梁的壁厚均有较大幅度的下降;上下框架的内梁壁厚都接近下限值;对接环上法兰的宽度增至 135mm.当基频下限取 11.8Hz时,结构质量上升.

5.2 改进设计

经过以上试算,该主承力桁架结构设计方向逐渐明确:①整星质心高度为 1.8m时,模态基频很难达到 11.0Hz,整星质心高度调整至 1.6m较为合理;②主支架圆管梁壁厚对结构刚度的影响大;③内埋梁中,次隔板的内埋梁对结构刚度影响最大,主隔板内埋梁的尺寸应有所不同;④应增大对接环上法兰的宽度(设计变量 8);⑤上下框架内梁的壁厚(设计变量 10,11)可减小.

由此,提出以下改进设计:①平台底板由初始的中心开口加下框架的设计改为封闭结构,从而去掉底板处的主隔板内埋梁 4,5和下框架;②设计变量 8由 100mm增至 130mm,不再参与优化.主隔板和次隔板的内埋梁由圆管梁改为接近实际结构的薄壁矩形梁,取其宽和高分别为 70mm和28mm,对应的壁厚分别为 t1=2 mm和 t2=0.7mm,其中 t1作为设计变量,分组见图 2b.

5.3 再优化

以 11.0Hz为基频约束,再次进行优化计算.此时,为了获得合理的结构参数,设计变量的寻优区间缩小,其上下限和优化结果见表 3.目标函数(结构质量)的优化迭代过程见图 3,其中 W为可优化部分的结构质量,初值为 372.8kg.

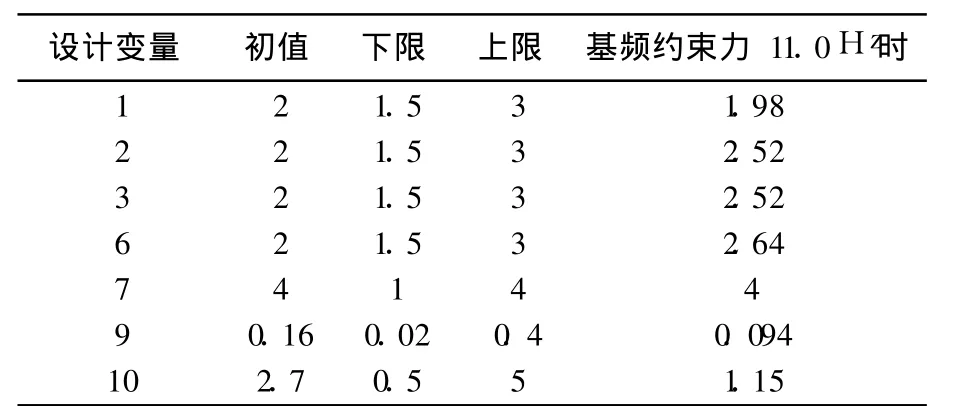
表 3 改进方案优化结果 mm

可见,改进方案优化后基频由 10.79Hz提高到 11Hz,重量则减轻了 3.2kg,显示了优化的效果.优化中,结构模态基频仍是临界约束,第 2种过载工况下的应力峰值最大,为 149MPa,远小于材料的强度极限.对优化后的结构进行校核,纵向模态频率为 34.27Hz(＞30Hz),第 2种过载工况下的最小临界稳定性系数由初始的 2.02增至2.21(＞1.5).可见,优化后结构的刚度、强度和稳定性均满足设计要求,可作为卫星初样详细设计的参考.

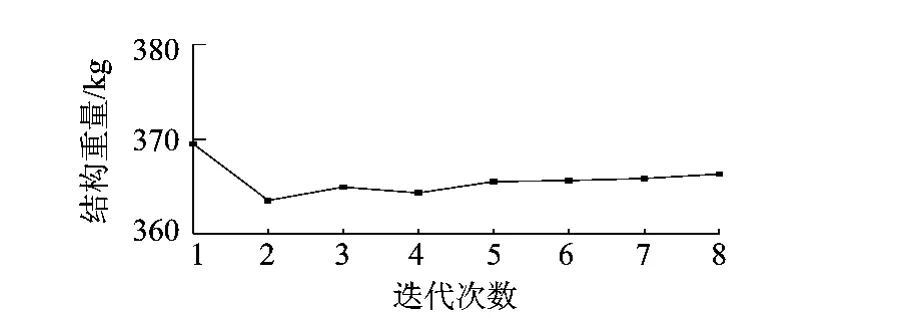
图3 目标函数(结构质量)迭代曲线

6 结束语

本文基于二级多点逼近优化算法,对某新型卫星主承力桁架结构初样方案进行了优化设计.经过初步试算、设计改进和再优化 3个阶段,逐步明确了设计的方向和各结构参数的取值范围,得到了合理的可行方案,为该卫星平台结构初样的详细设计提供了参考;同时也表明了该优化算法的可行性和有效性.

References)

[1]Woo T H.Structural optimization of large spacecraft[R].AIAA 1992-1227,1992

[2]陈珅艳,黄海,王利民.人机交互的航天器结构优化设计[J].计算力学学报,2004,21(4):510-512 Chen Shenyan,Huang Hai,Wang Liming.Structural optimization of spacecraft with man-machine interaction[J].Chinese Journal of Computational Mechanics,2004,21(4):510-512(in Chinese)

[3]顾元宪,亢战,赵国忠,等,卫星承力筒复合材料结构的优化设计[J].宇航学报,2003,24(1):88-91 Gu Yuanxian,Kang Zhan,Zhao Guozhong,et al.Optimal design of composite structure of bearing cylinder[J].Journal of Astronautics,2003,24(1):88-91(in Chinese)

[4]Huang H,Xia RW.Two-level multipoint constraint approximation concept for structural optim ization[J].Structural Optim ization,1995,9(1):38-45

[5]陈珅艳,袁家军,黄海.基于 MSC.PATRAN/NASTRAN的结构优化系统[J].宇航学报,2005,26(4):514-518 Chen Shenyan,Yuan Jiajun,Huang Hai.Structural optimization system based on MSC.PATRAN/NASTRAN[J].Journal of Astronautics,2005,26(4):514-518(in Chinese)

[6]盛聪,柴洪友,高峰,等.一种梁板复合结构的设计[J].航天器工程,2009,18(2):62-67 Sheng Cong,Chai Hongyou,Gao Feng,et al.Design of A kind of combined structure of beam and plate[J].Spacecraft Engineering,2009,18(2):62-67(in Chinese)

(编 辑 :张 嵘)

Structural optimization o f spacecraft based on two-level multi-point approximate method

Chen Shenyan Huang Hai

(School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

At the primal design stage of a new satellite,finite element model of the initial structure was established.Taking thicknesses of pipe beams and rectangle thin-wall beams as design variables,and considering constraints of natural frequency and strength,a structural optimization model was developed to approach minimum mass.Two-level multi-point approximation method was applied in structural optimization.In each calculation cycle,the original optimization problem was transformed to a first level multi-point approximate problem,and it was also approached by a second approximate problem which can be quickly solved by dual method.Three stages were implemented in the whole optimization process:initial optimum searching tests,design revision and re-optimization.Among the first stages,five runs were set with different constraints,design variables bounds and structural centroid heights,through which the design direction and interval of various structural parameters were obtained.Then the original structure was revised according to the results of the first stage.A new optimization model with fewer design variables and more reasonable variables bounds is established in the third stage and a feasible design is achieved,which provide references to detail design of the satellite structure.It indicates that the app lied design procedure and optimization method are effective in engineering structural optimization problem.

structural optimization;satellites;engineering;applications

V 414.19

A

1001-5965(2011)02-0237-04

2009-12-16

陈珅艳(1974-),女,浙江东阳人,讲师,chenshenyan@buaa.edu.cn.