小孔径多级孔板组件节流效应仿真
刘万龙 梁国柱
(北京航空航天大学 宇航学院,北京 100191)
徐 铭 张化照
(北京宇航系统工程研究所,北京 100076)
小孔径多级孔板组件节流效应仿真
刘万龙 梁国柱
(北京航空航天大学 宇航学院,北京 100191)
徐 铭 张化照
(北京宇航系统工程研究所,北京 100076)
对小孔径多级孔板组件(简称多级孔板)节流效应进行仿真研究,发现这类仿真对初场要求非常严格,初场不合理很容易产生伪平衡问题,通过迭代计算寻找合理初场的方法解决了该问题.同时对孔径 0.1mm、孔径比 0.025的多级孔板进行了数值仿真,仿真结果表明孔板数是影响多级孔板流量系数的主要因素.根据仿真数据给出多级孔板流量系数拟合公式,可以应用于工程设计计算.
孔板;流动仿真;节流;流量系数
小孔径孔板广泛应用于运载火箭管路系统中.由于孔板流量主要由孔板面积和压差决定[1],某型火箭排气冷却装置使用多个孔径 d=0.1mm、孔径比(节流孔与连接管内径之比)β=0.025的孔板同轴串联,逐级降低气体总压,提高节流效果.本文针对该结构的节流效应展开研究.
目前国内已有较多关于多级孔板水流消能的研究,文献[2]提出了多级孔板防止气蚀的设计方法,文献[3-6]对不同孔板消能设计方案的消能效率、流速分布等方面进行了室内或原型的试验研究,众多研究都表明多级孔板有很高的消能效率,但这些研究的对象都为大孔径、高孔径比多级孔板的水流研究.国内还没有针对小孔径、低孔径比多级孔板组件(简称多级孔板,下同)空气流动的研究.
1998年 ISO推出了 Reader-Harris/Gallagher孔板流量系数公式[7],但其适用范围为 50mm≤D(管路内径)≤1000mm,d≥12.5mm,0.1≤β≤0.75.对于 D<50mm,d<12.5mm,β<0.1的孔板流量系数,目前国际上尚无统一的数据[8].
这类小孔径、低孔径比多级孔板,试验研究困难,而且花费很大,故本文采用 Fluent软件对其进行仿真研究.在仿真过程中发现这类仿真对初场要求非常严格,初场不合理很容易产生伪平衡问题.本文通过寻找合理初始流场的方法解决了该问题,同时对孔径 0.1mm、孔径比 0.025的多级孔板进行了数值仿真.为提高工程设计效率,避免复杂的流场仿真,根据仿真数据本文将给出具有物理意义的拟合方程,为进一步的工程设计计算、试验提供指导和数据支持.
1 计算模型和边界条件
1.1 物理模型
图1为 3级孔板物理模型示意图(为显示方便,孔板孔径作放大处理).如图所示多级孔板基准参数为:孔径 0.1mm,管路内径 4mm,孔板厚度2mm,孔板间连接管路长 8mm,入口段长 25mm,出口段长 34mm.其他多级孔板与图 1仅孔板数量不同,其他结构参数一致.工质为空气,背压101325Pa,环境温度 293K.

图1 3级孔板物理模型示意图(单位:mm)
1.2 网格划分
采用轴对称计算模型,由 Gambit软件生成网格.由于本模型为多级孔板,孔径比为 0.025,对网格进行了特别的处理:
1)对直径变化剧烈区域通过调整比例系数进行局部加密;
2)对各个管路及孔板进行单独网格分区,以便分区赋值.以 32级孔板为例,共划分了 65个分区,生成 223960个矩形网格,孔板与连接管路局部网格如图 2所示.

图2 孔板与连接管路局部网格
1.3 边界条件及计算方法
采用压强入口及压强出口边界,入口表压为21MPa,出口表压为 0.控制方程组为雷诺平均 NS方程组,采用耦合隐式稳态求解器,湍流模型为2阶标准 k-ε两方程模型[9].对壁面方程采用增强壁面处理方式处理,并考虑压强梯度的影响.对动量方程、湍流动能方程、湍流动能耗散率方程均采用二阶迎风格式离散.
2 伪平衡问题的发现及解决
2.1 伪平衡问题及物理解释
通过仿真发现:这类小孔径、低孔径比多级孔板模型计算中会出现伪平衡现象,即在各项残差都很低,残差和各孔板流量都很稳定时,各个孔板的流量相差很大,流场实际还没有达到最终的稳定状态.
以 5级孔板为例,用以下参数初始化流场:表压 21MPa,温度 293K,轴向速度 0.18m/s,径向速度 0,湍流动能 7.6×10-5m2/s2,湍流动能耗散率3.9×10-4m2/s3.计算中当各项残差都小于10-4,并基本保持不变时,得到各级孔板流量分别为 3.57×10-5,2.95×10-6,1.04×10-7,2.85×10-6,2.91×10-4kg/s,最大流量为最小流量的2798倍.对流场压强取样,发现此时除了出口段管路压强降至与背压一致,末级孔板内部表压从21MPa向 0梯度下降外,其他管路及孔板内的压强基本不变,维持在初始表压 21MPa附近,这不符合多级孔板的实际流动过程.
算例中管路截面积为孔板截面积的 1 600倍,相对于孔板,管路是一个巨大容腔.该物理过程相当于气体从气源经过若干个由细小孔板连接的巨大容腔向外放气.计算的初始状态相当于容腔末端封闭,各个容腔内气压与气源一致.开始计算后相当于打开容腔末端,末级容腔(出口段)压强很快与背压一致,末级孔板内有较大压强梯度,而其他孔板及管路内的压强还维持在气源压强.此时末级孔板上游的其他孔板尽管流量差别还很大,但是由于这些孔板流量的绝对数值极小,对流场压强调整很慢,因此需要相当长的计算时间才能达到最终平衡.
2.2 伪平衡问题解决方案
通过实际计算发现,达到伪平衡状态后很难通过延长计算时间或调整 courant数来得到准确计算结果.本文通过不断采用更精确的初场对流场各部分重新初始化的方法解决了该问题.在孔板组件中,相对于入口压强,背压很小,空气经过各级孔板时静压减少,速度增加,在末级孔板出口出现音速,需用到可压流的流量方程及临界流的流量方程式(1)和式(2).使用流量方程及质量守恒方程式(3)迭代求解,配合 Fluent进行计算.

式中,m·为孔板质量流量;Cd为孔板流量系数;A为孔板面积;k为气体比热容比;p1为孔板入口总压;p2为孔板出口静压为临界状态下孔板流量;R为通用气体常数;T为空气总温为第 i级孔板流量;n为总孔板数(n>1).
具体计算流程如下:
1)设定各孔板流量系数及各个管路压强的初值(由于管路中气体流速很低,采用静压代替总压);
2)迭代计算求得各孔板流量一致时的各管路的压强值;
3)用这些压强值初始化 Fluent流场,计算得到此时各个孔板中的气体流量;
4)把流量代入式(1)、式(2)得到修正后的流量系数;
5)如果此时各孔板流量不一致,回到步骤2),用新的流量系数计算得到各孔板流量一致时各管路的压强值,代入 Fluent求解流量,继而求得新流量系数;
6)反复初始化流场和修正流量系数,直至Fluent计算出来的各孔板流量偏差满足精度 10-5的要求.
3 计算结果及数据分析
3.1 拟合曲线及拟合公式
由于末级孔板出口处气流速度为音速,可把多级孔板当成一个音速节流装置.应用式(2)可得:多级孔板组件流量系数 Cdu(简称组件流量系数,下同)等于前 n-1级孔板的总压总恢复系数σ(简称总压恢复系数,下同)与末级孔板的流量系数 Cdn的乘积,Cdu=σCdn.
来流雷诺数 Re(Re=4m·/(πμD),μ为动力粘度)是流量系数拟合常用的修正参数,图 3为仿真得到的 Cdn与 Re关系图,从图中可以看出随着Re的增大,Cdn呈增大趋势,但变化幅度不大,Cdn分布在一条直线附近,式(4)为其拟合公式.
图4为 σ及 Cdu随 n的变化图,从图中可以看出 σ及 Cdu对于 n遵循类似幂函数的分布规律.随着 n的增大,σ及 Cdu初始下降迅速,后来逐渐趋缓.这种现象符合空气动力学原理,因为孔板对气流的阻力与气流速度的平方成正比,随着 n的增大,多级孔板内气流速度下降,新增孔板对气流的阻滞作用越来越弱.
由仿真数据可知当 n>11时,Cdu随 n变化率小于 0.015,此时 n的变化对 Cdu影响已经很小,很难再通过增大 n来大幅改变 Cdu.式(5)、式(6)分别为 σ及 Cdu的拟合公式.由图 3、图 4可以看出 n是影响 Cdu的主要因素.
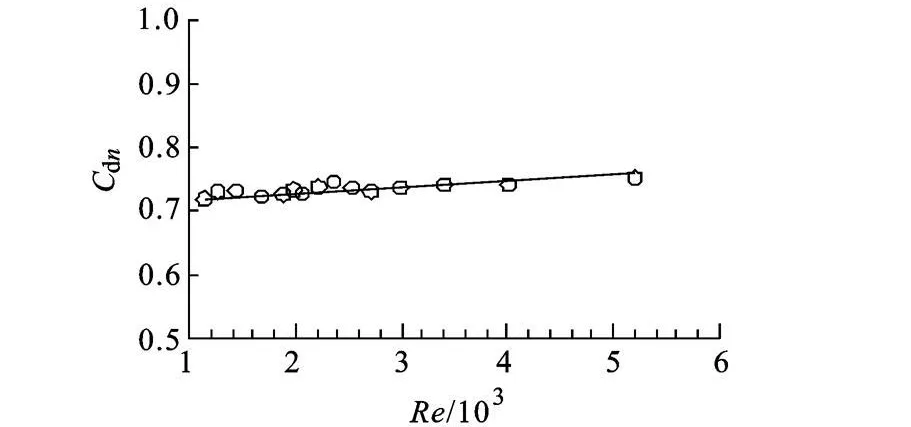
图3 末级孔板流量系数与雷诺数关系图
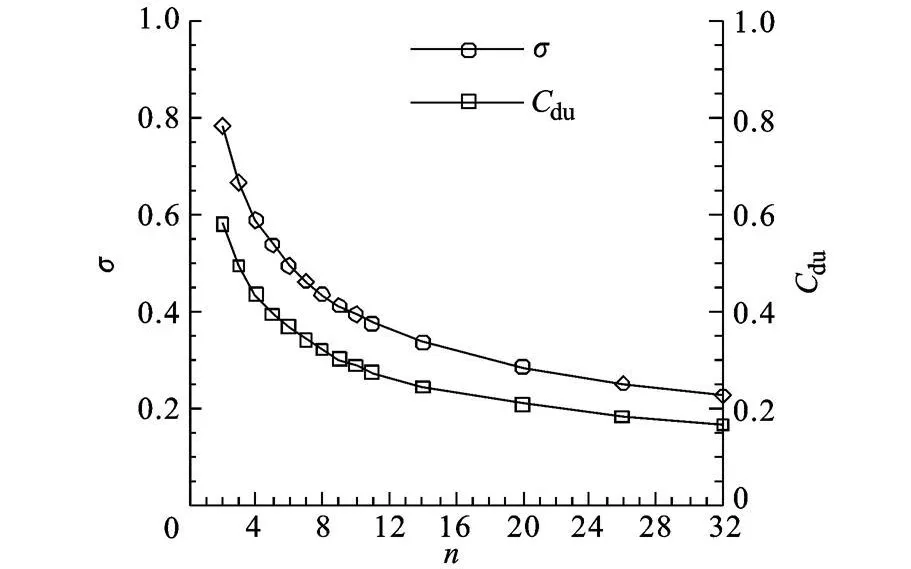
图4 总压恢复系数及组件流量系数随孔板数变化图
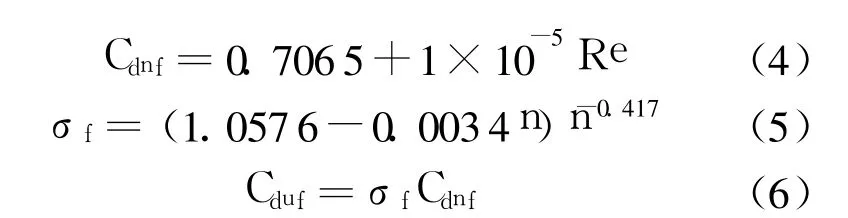
式中,Cdnf,σf,Cduf分别是 Cdn,σ,Cdu的拟合值.
3.2 拟合公式精度及适用范围
表 1为入口表压 21MPa时 Cduf的精度分析.表中给出了仿真得到的各多级孔板 Cdu,Re,σ,Cdn及拟合公式得到的 Cduf.如表所示 2~32级孔板Cdu与 Cduf偏差范围为 -1.89%~1.49%.为了验证拟合公式对不同入口压强的通用性,选用不同的入口表压:2.5MPa,10.3MPa,10.4MPa,对不同多级孔板进行仿真.得到的拟合值与仿真值对照如表 2所示,2~32级孔板 Cdu与 Cduf偏差范围为 -1.91%~0.78%.此偏差范围与表 1的情况基本一致,表明此公式对不同的入口压强有通用性.拟合偏差小于 2%,可以应用于工程设计计算.
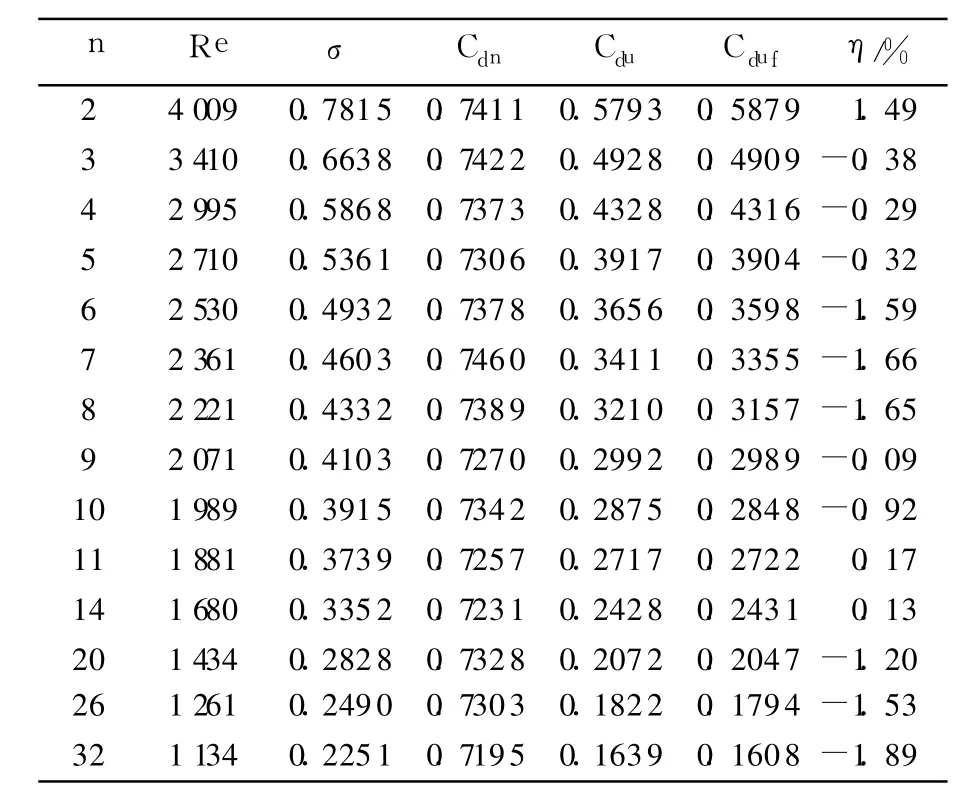
表 1 入口表压 21M Pa时组件流量系数拟合值精度分析
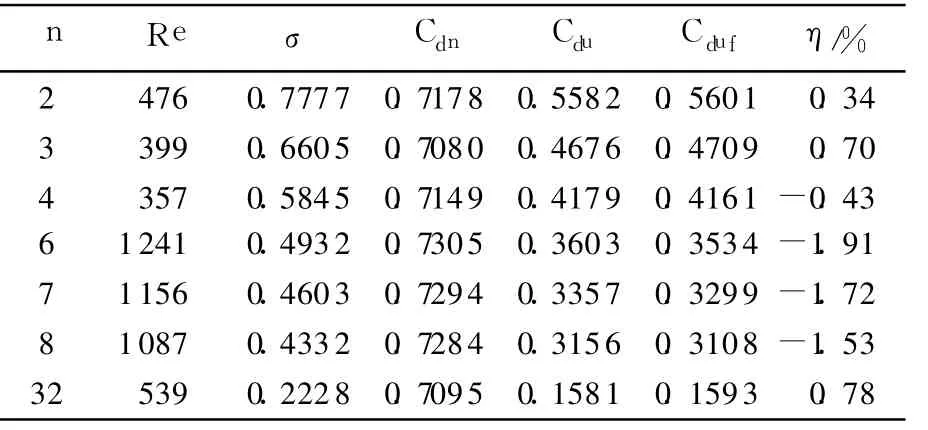
表 2 不同入口压强下组件流量系数拟合值精度分析
4 结 论
1)本文通过迭代修正孔板流量系数及寻找合理初始流场的方法解决了多级孔板组件流场仿真中的伪平衡问题.
2)在本文研究范围内,随着来流雷诺数增大,孔板组件末级孔板流量系数呈增大趋势,但变化幅度不大.
3)孔板数是影响多级孔板组件流量系数的主要因素.组件流量系数对于孔板数遵循类似幂函数的分布规律,随着孔板数的增加,组件流量系数初始迅速下降,后来逐渐趋缓.当 n>11时,组件流量系数随孔板数变化率小于 0.015.
4)给出适用于工程应用的前 n-1级孔板的总压总恢复系数、末级孔板流量系数、多级孔板组件流量系数的拟合公式,适用于入口表压范围为2.5~ 21MPa、孔径 0.1mm、孔径比 0.025、末级孔板出口为临界流或超临界流的多级孔板组件,拟合偏差小于 2%,可以应用于工程设计计算.
对于不同孔径、孔径比、孔板厚度、孔间距及其他介质下多级孔板的流量特性还有待于作进一步研究.
References)
[1]蔡武昌,孙淮清,纪纲.流量测量方法和仪表的选用[M].北京:化学工业出版社,2001:23 CaiWuchang,Sun Huaiqing,Ji Gang.Flow measurement methods and instruments choice[M].Beijing:Chemical Industry Press,2001:23(in Chinese)
[2]张宝峰.多级节流孔板的设计计算[J].西北电力技术,2005,33(5):27-30 Zhang Baofeng.The numerical design of multi-hole orifice[J].Northwest China Electric Power,2005,33(5):27-30(in Chinese)
[3]郭晓宇.多级孔板螺旋流消能装置试验研究[D].太原:太原理工大学水利科学与工程学院,2008 Guo Xiaoyu.Study on the effect of multi-orifices spiral flow energy dissipation equipment[D].Taiyuan:College of Water Resources Science and Engineering,Taiyuan University of Technology,2008(in Chinese)
[4]武鹏林,彭龙生.多级孔板消能效率初探[J].太原理工大学学报,1995,26(4):11-17 Wu Penglin,Peng Longsheng.Investigation of efficiency of energy consumption for step orifice plates[J].Journal of Taiyuan U-niversity of Technology,1995,26(4):11-17(in Chinese)
[5]刘群.多级孔板消能在大梁水库放水洞中的研究应用[J].水利水电技术,1994(9):2-7 Liu Qun.Research and application of multistage orifice energy dissipation in the dewatering tunnel of daliang reservoir[J].Water Resources and Hydropower Engineering,1994(9):2-7(in Chinese)
[6]赵慧琴.多级孔板消能系数问题探讨[J].水利水电技术,1993(6):45-50 Zhao Huiqin.Multistageper forated plates energy dissipation coefficient discussion[J].Water Resources and Hydropower Engineering,1993(6):45-50(in Chinese)
[7]Baker R C.Flow measurement handbook[M].Cambridge:Cambridge University Press,2000:128
[8]ISO/CD 5167-2—1999 Measurement of fluid flow by means of pressure differential devices inserted in circular cross-section conduits running full[S]
[9]王福军.计算流体动力学分析[M].2版.北京:清华大学出版社,2005:121-122 Wang Fujun.Computational fluid dynam ics analysis[M].2nd ed.Beijing:Tsinghua University Press,2005:121-122(in Chinese)
(编 辑 :张 嵘)
Simulation for throttling effect of small aperture multistage orifice units
LiuWanlong Liang Guozhu
(School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Xu Ming Zhang Huazhao
(Beijing Institute of Astronautical System Engineering,Beijing 100076,China)
Throttling effect of small aperture multistage orifice units was studied through simulation method.It was found that strict initial flow field was needed in this kind of simulation,and the simulation would be dummy-balanced with irrational initial flow field.This problem was solved by iterative finding proper initial flow field.The multistage orifice units with 0.1mm aperture and 0.025 aperture ratio were simulated.The simulation result shows that the number of the orifices is the major factor which influences the flow coefficients of the multistage orifice units.Fitted for mulae for the flow coefficients were given depending on the simulation results.The fitted for mulae can be applied to actual engineering design calculation.
orifice;flow simulation;throttling;flow coefficient
TB 937
A
1001-5965(2011)02-0241-04
2009-12-10
刘万龙(1982-),男,江苏盐城人,博士生,lw l8203@126.com.

