基于领域知识的冗余关联规则消除算法

张 晶， 张 斌， 胡学钢

(合肥工业大学计算机与信息学院，安徽合肥 230009)

关联规则挖掘技术目的在于发现新颖的、有用的、感兴趣的、隐藏在项目集合中的关联规则[1]。关联规则挖掘算法应该发现隐藏的、新颖的关联性。然而，大部分经典算法仅考虑数据本身[2，3]，而与数据相关的极为丰富的相关领域知识资源并没有作为先验知识来消除已知模式，导致挖掘的知识往往包含大量冗余的规则。关联规则挖掘算法把很多在领域中作为常识的已知关联知识提取了出来，造成知识大量的冗余。在关联发现中大部分研究集中在采取降低阈值的方法来降低规则数目从而达到消除冗余的效果。

所谓的领域知识[4]DK(dom ain know ledge，简称DK)，是指一个专门领域中的重要问题或概念以及这些问题或概念之间的相互关系。

在知识发现系统中，把加入的那些有关指导和限制搜索感兴趣的知识称为背景知识或领域知识，且一般不把两者进行区分。知识发现算法应该合理使用领域知识，以达到缩短搜寻时间的目的。领域知识是指有助于进行知识发现的信息，它不仅仅是一些应用领域内的业务知识，还包括知识发现相关知识以及其它相关背景知识等。知识发现应以领域知识为基础，利用领域知识有目标地进行知识发现，一方面可以缩小目标搜索范围，提高效率;另一方面可以提高发现模式或结果的兴趣度、可信度，同时兴趣度和可信度本身也与领域知识有关。

本文提出一种基于领域知识的关联规则算法DKARM，既考虑了数据本身具有的领域知识关系，又针对经典的关联规则算法进行了改进，同时对算法进行了理论分析和实验验证。

1 引入领域知识挖掘关联规则

由于某些事务项之间在领域知识的指导或约束下体现了众所周知的强依赖性，关联挖掘所得到的规则往往包含大量冗余的规则。如超市销售数据中，{钉子，锤子}之间具有强关联性，是一个可信度很高的规则。但这类规则对用户来说，可能并不感兴趣。用户感兴趣的是类似于{尿布，啤酒}这类无法在领域知识指导下得到的真正有趣的知识。在传统的关联规则挖掘中，大部分已挖掘出的规则可能与已知的领域知识存在强烈的联系，但是发现有用新颖的知识却不能借助这些规则。这样就造成了一种结果，那就是用户感兴趣和不感兴趣的关联规则交错在一起，这样用户为了发现感兴趣的模式不得不逐一区分和解释这类规则。

显然，在领域知识指导下能明显呈现出的关联规则被剔除在关联规则挖掘当中，则可以避免这类规则被用户所提取和看到。为了达到减少在关联规则挖掘中的已知模式的数目，本文提出了DKARM算法，使用领域知识作为先验知识，来消除冗余的关联规则及其派生规则。

1.1 关联规则基本模型

关联规则是支持度和置信度分别满足用户给定阈值的规则，所有支持度大于最小支持度的项集(Itemset)，称为频繁项集(Frequent Itemset)，简称频集。

发现关联规则主要分2个步骤:找出所有频繁项集;由频繁项集生成满足最小信任度的规则。

文献[2]首先提出了挖掘顾客交易数据库中项集间的关联规则问题，其核心方法是基于频集理论的递推方法。这是一种有效的关联规则挖掘算法，但它可能产生大量候选项集，且需要多次重复扫描数据库，大量的时间消耗在内存与数据库中数据的交换上。

文献[2]证明关联规则具有如下性质:

性质1 频繁项集的子集必定是频繁项集。

性质2 非频繁项集的超集一定是非频繁的。

针对Apriori算法的固有缺陷，文献[3]提出了不产生候选挖掘频繁项集的方法——FP-树频集算法。采用分而治之的策略，建立了基于FP-tree频繁项模式的无候选项集的结构思想，将原始数据库中的每一项事务都压缩到一棵FP-tree中，从而大大降低了FP-G row th算法的挖掘耗时，提高了挖掘效率。但FP算法仍存在一定的局限性，它通过递归创建条件模式来挖掘频繁项，如果树中分枝较长时，这个递归过程仍很费时。

1.2 实例分析

通过实例分析没有消除明确的领域知识指导下的强关联性规则挖掘问题。考虑元素集合 Γ= {A，B，C，D，E}，这些元素所有可能的组合集为: {AB}、{AC}、{AD}、{AE}、{BC}、{BD}、{BE}、{CD}、{CE}、{DE}、{ABC}、{ABD}、{ABE}、{ACD}、{ACE}、{ADE}、{BCD}、{BCE}、{BDE}、{CDE}、{ABCD}、{ABCE}、{ABDE}、{ACDE}、{BCDE}、{ABCDE}。不考虑任何阈值，可能的子集数目是26，这些子集产生的最大规则数是180。

下面考虑元素C和D在领域知识指导下有强关联关系。值得注意的是，C和D同时出现的有8个集合({CD}、{ACD}、{BCD}、{CDE}、{ABCD}、{ACDE}、{BCDE}、{ABCDE})。这8个集合将产生92个规则，在每个规则中，C、D都同时出现，结果是整个规则的51.11%将由C和D之间的关联性而产生。

非常重要的一点是，不能在预处理工作中直接从Γ中删掉C和D，因为C或者D都可能和A、B或者E有关联。然而，在同一集合中，应该能避免C和D的组合，这就消除了产生的规则同时包括C和D的可能性。

1.3 基于领域知识的关联规则挖掘算法

为了便于展开研究，冗余规则限定为只包含2个事务项(ITEM)，这2个事务项称为冗余项对。超市商品交易数据库见表1所列。

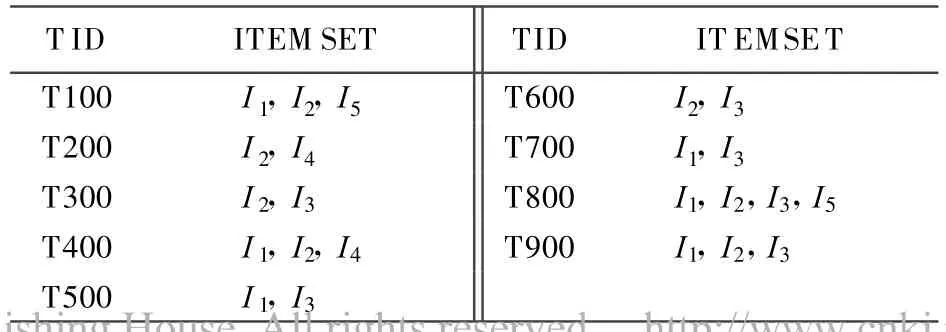
表1 超市事务数据库

1.3.1 算法DKARM描述

输入:事务数据库D，最小支持度计数m insup，领域知识指导下的冗余项对Ω。

输出:消除了冗余项对的频繁模式集合P。

(1)扫描一遍数据库D获得1-候选集，删除频率小于最小支持度计数min_sup的项，获取所有频繁项，得到1-频集，并将1-频集中各项按支持数递减排列。由表1得到的支持度计数结果按降序排列，见表2所列，并将数据库中每一项事务根据1-频集中的次序重新排序后得到L，见表3所列，这是有效合并重复路径的前提。

(2)第2次扫描数据库L，构建带有分支编号的FP-tree。

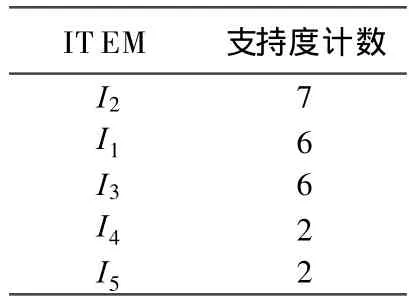
表2 计数结果(1-项集)

表3 重排列的数据库L

首先创建树的根节点，以“NULL”标记它;接着，第2次扫描数据库，按照L中的次序，将数据库中的事务依次插入到根节点下。根据表3得到的带分支编号的FP树，如图1所示。如结点I3:2(12)表示在I3结点的支持度计数是2，分支编号用括号中的字符串表示，“12”表示结点I2在从根开始的第1分支的第2子分支中。

(3)依次从各分枝开始从根往下挖掘与该分枝中的第1项组合的2-项集，并依次统计各分枝中该项的支持数，结合min_sup，得到2-频集。如图1中从“NULL”结点开始，I2结点得到的2-项集{I2 I1:4(11)，I2 I3:2(12)+2(112)，I2 I4: 1(13)+1(113)，I2 I5:1(111)+1(1221)}，I1结点得到的2-项集为{I1I3:2(112)+2(21)，I1 I5:1(111)+1(1221)}。依次按表2中结点的顺序再如此计算I3、I4、I5结点。假设最小支持度计数为2，则可得{I2I1:4(11)，I2I3:2(12)+ 2(112)，I2 I4:1(13)+1(113)，I2 I5:1(111)+ 1(1221)，I1 I3:2(112)+2(21)，I1 I5:1(111)+ 1(1221)}均为2-频繁项集。

(4)在所有的2-频集中删除领域知识指导下得到的冗余项对集合 Ω。

(5)根据Apriori性质，由K-1阶的项集可构造K阶的候选项集，直到某一阶的项集为空，得到所有消除了冗余项对的频繁模式集合P，算法停止。

由于2-项集中保留了每项事务在每个分支中的支持数，因此在2-项集的基础上可直接得到3-候选集的支持数，而不必再次扫描原数据库或者递归访问 FP树。如{I2I1:4(11)，I2I3: 2(12)+2(112)，I1I3:2(112)+2(21)}是2-频繁项集，所以3-项集{I2 I1 I3}也是频繁的，根据其分支编号共享的前缀，可得其支持数为2，即得{I2I1I3:2(112)}。

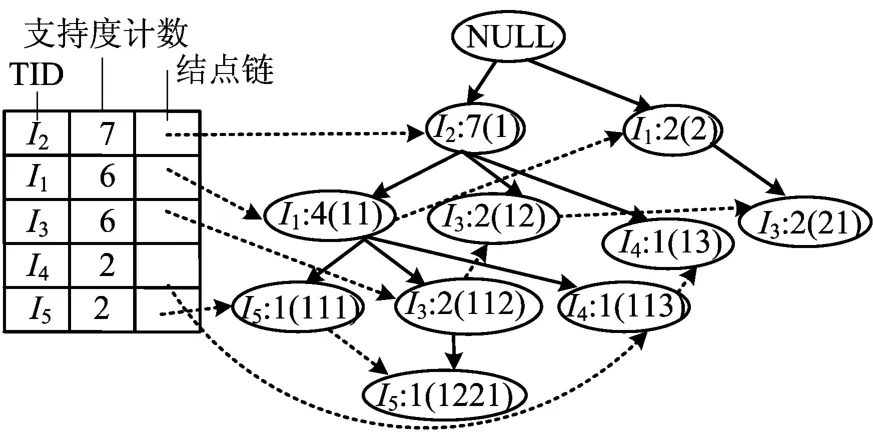
图1 带分支编号的FP树

1.3.2 算法说明

第1步和第 2步基本和FP树算法保持一致，但是在形成FP树时增加了分支编号，以便后续步骤中更高阶项集的信息获取。

第3步在2-项集的搜索中没有沿用FP树常用的自底向上方法，而是自顶向下进行项的组合。

第4步中，当产生2个元素的候选集后，所有Ω中冗余的元素对都从2-频集中删除。由于这一步骤中消除了 Ω中的每个来源于领域知识的冗余项对(如{C，D})，不仅避免产生规则C→D，而且也避免产生所有派生规则(如{D→C，C→AD})，这些规则也包含已知强关联性。根据性质1和性质2，保证了 Ω中冗余项对不会在后续频繁项集合中同时出现，也将不会在关联规则中出现，使得此方法很有效，而且独立于任何最小支持度、最小置信度等阈值的限制。这种方法消除所有的包含冗余项对的候选集合，而独立于任何概念层次，这是本算法不同于其它消除冗余规则算法的特点[5，6]。

在前2个步骤中，利用FP算法将原始数据库中的每一项事务都压缩到一棵FP-tree中，避免了多次扫描数据库;第5步利用了Ap riori算法的核心思想。根据Apriori性质，在2-项集的基础上通过链接与剪枝可得到更高阶的项集;通过FP树中增分支编号，在获取2-项集时保留了每项事务在每个分枝中的支持数，因此，在2-项集的基础上可以直接得到3-候选集的支持数，而不必再次递归访问FP树。因此，DKARM算法既可避免Apriori算法中多次扫描数据库不断产生候选项的缺点，又克服了FP-Grow th算法中的递归挖掘方式。

值得说明的是，在DKARM算法中，领域知识指导下的冗余对是作为已知输入直接获取的。针对领域知识获取与数据挖掘的融合工作，很多学者展开了一系列研究，参见文献[7-9]。

2 评 估

不考虑最小支持度和最小可信度的阈值，图2所示给出了消除不同数目的冗余项对后得到的规则数的理论计算结果，理论分析中事务项个数为2～12的事务数据库。其中，分别讨论了0对、1对、2对冗余项对从集合中消除，0对即为不消除冗余规则得到的结果。

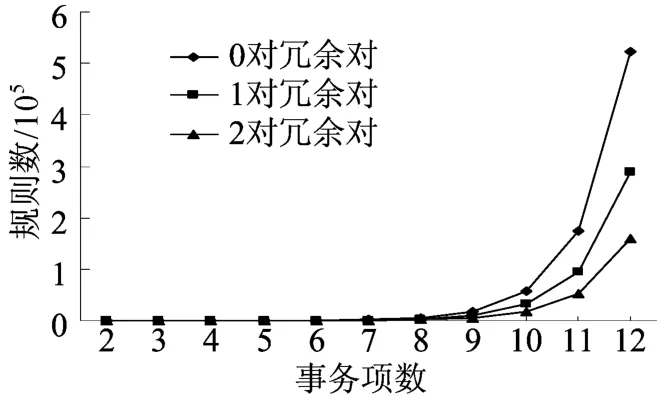
图2 消除不同数目的冗余对的规则数分布图

从这3种情况可以看出，不消除冗余的规则数目随着集合中的元素数目的增加呈指数形式增长，而消除冗余后能够大大减少产生规则的数目。

显然，如果冗余项对的数目越多，这种方法的作用也就越明显。

图3所示给出了当被消除的冗余项对的数目为0、1、2时，减少规则占总的规则的百分比。如当消除1个冗余项对时，产生的规则仅占总规则数目的55%，而被消除的已知规则占45%;当消除的依赖对的数目为2时，仅有30%的规则产生，而被消除的规则增加到70%。

不难看出，随着事务项数目的增加，曲线趋向于饱和值。

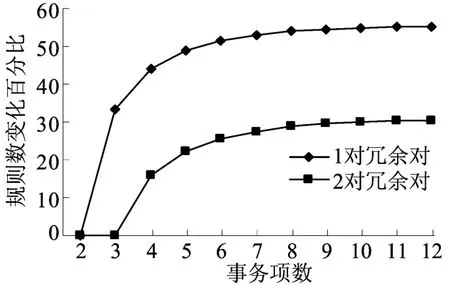
图3 规则数变化百分比分布图

同时，在 W indow s XP、CPU Intel T2050 1.60 GH z、内存1.00GB环境下，使用Java语言实现了DKARM算法。采用来源于文献[1]中的A llElectronics某分店的事务数据(包括9个事务数和5个项数)、Weka生成的RDG1(100个事务数和10个项数)和contact-lenses(包括24个事务数和12个项数)进行实验，实验中设置支持度为20%，置信度为60%，得到的实验结果见表4所列。

从实际数据的验证结果可知，规则数和时间明显降低了。对于数据挖掘的用户来说，消除领域知识指导下的已知规则比降低产生关联规则的计算时间更为重要，充分考虑数据相关的领域知识对挖掘过程的指导意义，这是本文的主要目的。然而，随着具有关联的依赖对集合的消除，较少的候选集将会产生，因此产生规则的计算时间也随着减少，这也是必然的结果。

表4 DKARM算法实验结果m s

3 结束语

本文以领域知识作为指导，提出可消减冗余关联规则数目的挖掘方法，可以在某种程度上保证产生的规则对用户来说更感兴趣，这种消减并不受最小支持等阈值的影响。在有关领域知识指导下，如何获取更复杂的项之间关系作为先验知识指导后续的挖掘工作，如何更有效地评估挖掘后规则的兴趣度，都是进一步的研究工作。

本文初稿首次刊登于《计算机技术与应用进展◦2010》

[1] Han Jiaw ei，Kamber M.Data m ining-concepts and techniques[M].M organ Kaufman Publishers，2001:1-30.

[2] Agrawal R，Imielinski T，Swami A.M ining association ru les betw een setsof item s in large databases[C]//Proc of the ACM SIGMOD Conference on M anagem ent of Data，1993: 207-216.

[3] Han Jiaw ei，Pei Jian，Yin Y.M ining frequent patterns withou t candidate generation[C]//Proc of the ACM SIGMOD Conference on Management of Data，2000:1-12.

[4] Fayyad U，Piatetsky-Shapiro G，Smyth P.From datam ining to know ledge discovery:an overview[C]//Advances in Know ledge Discovery and Data M ining.M enlo Park，California:AAA IPress，1996:1-35.

[5] ZakiM.Generating non-redundan t association rules[C]// Proc of the 6th ACM-SIGKDD International Conference on Know ledge Discovery and Data M ining，Boston，M assachusetts，USA，2000:34-43.

[6] Liu B，H su W，Ma Y.Pruning and summarizing the discovered associations[C]//Proc of the 5th ACM-SIGKDD International Conference on Know ledge Discovery and Data M ining，San Diego，California，1999:125-134.

[7] 邢平平，施鹏飞，赵 奕.基于本体论的数据挖掘方法[J].计算机工程，2001，27(5):15-17.

[8] 钟佩思，徐文胜，曾庆良，等.领域知识获取与有效性检查过程集成研究[J].机械科学与技术，2001，20(5):798-800.

[9] 谢 亮，张 晶，胡学钢.主从关系数据库中关联规则挖掘算法研究[J].合肥工业大学学报:自然科学版，2009，32 (5):663-666.