气动管道中压力波的传播特性分析

林惟锓 黄 亮 蔡茂林

(北京航空航天大学自动化科学与电气工程学院，北京 100191)

气动管道中压力波的传播特性分析

林惟锓 黄 亮 蔡茂林

(北京航空航天大学自动化科学与电气工程学院，北京 100191)

利用一维非定常气流理论，建立了管道中气体传播的分布式参数模型，采用迎风差分的方法进行数值计算，并通过实验结果与模型仿真结果的比较，验证了该模型的正确性.通过改变管道直径、气源速度、入口压强和仿真空间步长等初始条件，模拟不同特性的管道，对仿真结果进行比较分析，得到不同波形的压力波在不同管道中传播的特性.结果表明:利用压力波测流量时，应采用下弦波或矩形波.

非定常气流;迎风差分;压力波;传播

压力波是指流场中某一局部区域或某一点处发生的微小扰动传递到其他区域的一个波动传播过程［1］.国内外主要针对气液两相流、燃烧系统、隧道等方面研究压力波的特性.文献［2］对压力波的传播进行了实验测量;文献［3］测量了管道内气液两相流动的压力波传播速度;文献［1］对压力波的色散特性进行了研究分析;文献［4］采用了一维非定常流模型研究隧道压力波;文献［5］利用湍流模型研究了高速列车交会时压力波的计算方法.然而对工业气动管道中压力波传播的研究较少.

低碳时代的到来，对工业节能提出了严峻的考验.气体流量作为气动系统的一个重要参数，对其准确的测量是关系工业控制质量和企业经济效益的关键问题，因此研究管道中气体流量测量方法具有重要的实际意义及明显的经济效益.文献［6］提出了一种利用压力波的传播进行并联式的管道流量测量的方法:以压力波和气体在管路中的传播特性为基础，在相同距离的条件下，利用管道上下游的压力波产生装置分别产生两个传播方向的压力波，通过测量压力波传播时间的变化量来计算管路中气体的流量.只有掌握了管道中压力波的传播特性才能提高该测量方法的精度.因此本文采用一维非定常气流模型，通过计算机仿真，定性分析气动管道中压力波的传播特性.

1 管道气流动态模型的建立

1.1 气动管道系统动态模型

假定管路内气体流动为一维流动，在考虑管壁与气体之间热量传递的基础上，应用一维非定常气流理论，可以建立精确的气动管道系统分布式参数模型［7－8］，该模型由4组方程式组成.

状态方程式为

式中，P为空气的压力，Pa;ρ为空气的密度，kg/m3;R为气体常数，对于空气，R=287 J/(kg·K);θ为空气的绝对温度，K.

运动方程式为

式中，u为空气的流速，m/s;λ为管路内壁的摩擦系数;D为管路的内径，m;x为流动方向的坐标，m;t为时间，s.

连续方程式为

能量方程式为

其中

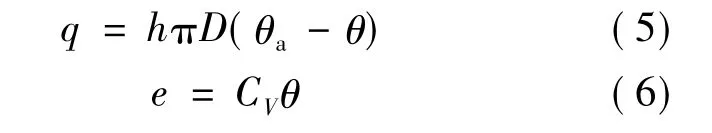
式中，A为管路的截面积，m2;q为空气与外界的热交换量，J/m;θa为大气绝对温度，K;CV为空气的等容比热，CV=718 J/(kg·K);e为单位质量气体的内能，J/kg;h为空气与管壁间的传热率，W/(m2·K).

将式(5)、式(6)代入式(4)中，并利用式(1)～式(3)整理可得

λ和h分别由下式确定:

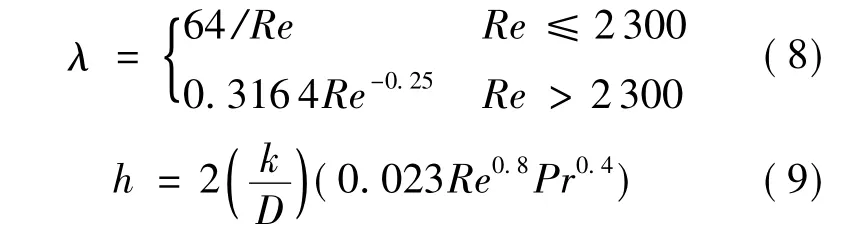
式中，Re为雷诺数;k为空气的热传导率，k=7.95×10－5×θ+2.046 5 ×10－3;Pr为普朗特数，Pr=0.72.

由式(2)、式(3)、式(7)可以求出管道内气流沿传输线在任意点、任意时刻的3个状态量:u，ρ，θ，再用式(1)即可确定P.该模型考虑了气体的压缩性及气体与管壁之间的热交换，是一个普遍适用的精确的一维管道气体流动模型.

1.2 管道气流动态模型的离散化

为了对上述模型进行计算机仿真，先对其基本方程离散化.本文采用双曲型方程的迎风差分格式［9－10］进行离散化.

状态方程式为

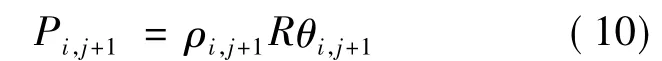
式中，i为等分格子的编号;j为时间步数.

运动方程式为

式中，Δt为时间步长，s;Δx为等分格子的长度，m;对流项 u∂u由 uconv表示为

连续方程式为

式中，对流项 u∂ρ由 ρconv表示为

能量方程式为

式中，对流项 u∂θ由 θconv表示为

2 管道气流传输仿真

基于上文所建立的模型，利用C语言进行编程仿真，如图1所示.

仿真过程将管路长度L=20m等分为20份，即Δx=1m;仿真时间T=4 s，等分为100 000份，即 Δt=4×10－5s.由式(10) ～式(13)可知，为计算下一时刻某一模块的状态量，须知道该时刻对应模块及其前后各一个模块的状态量.因此，为计算第1块和第20块的状态量，还必须设出虚拟的模块0和模块21.对于模块0，P为输入的压力值，θ取室温(假设室温为 20℃，则 θ=20+273.15=293.15 K)，ρ可以由式(1)得到，u 是设定的固定值;对于模块21的状态量P，θ，ρ和u均与上一时刻其旁边模块的对应值相同.

本仿真的目的是通过设定不同的仿真条件:输入波形分别为矩形波、三角波、正弦波、下弦波;L 分别为 20，15，10，5m;D 分别为 0.009，0.025，0.050，0.100m;P 分别为 0.8，0.7，0.4MPa;u 分别为 5，10，15，20m/s等 5 个方面，模拟不同形状的压力波在不同的条件下的传播特性.

3 仿真结果及分析

仿真图中Pi表示i模块的压力信号，P0即为输入的压力波，P20即是传播到下游的压力波.

3.1 实验验证

按图1的方法连接管路，使上游的电磁比例阀导通0.5 s后关闭，上游产生的矩形压力波沿管道向下游传播.L=20m，D=0.050m，u=5m/s，结果如图2所示.图2中，P20是利用PU作为输入，通过仿真计算得到的结果.

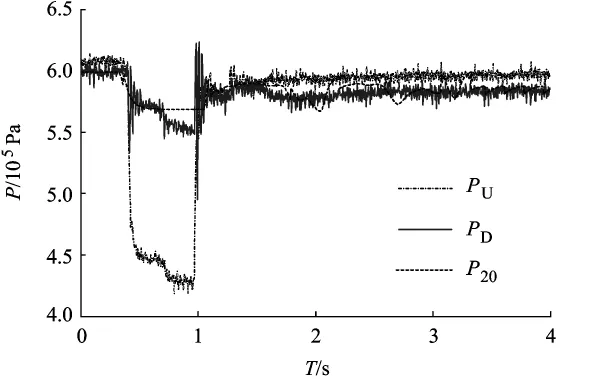
图2 实验结果与仿真比较

图3为每一时刻P20跟PD的相对误差，最大的相对误差值为14.83%，平均的相对误差为5.12%.由于实验过程中受电磁阀响应，管道表面粗糙，而且存在管道弯头等因素的影响，压力波会有较明显的衰减，而仿真过程中忽略这些因素的影响，所以存在误差，但误差值在允许范围内，证明了本仿真的正确性.

图3 仿真结果的相对误差

3.2 压力波为矩形波

在比较中，以 P0=0.81MPa，经过 0.8 s后压强下降到 0.6 MPa，并持续 0.2 s，再 回 到0.81MPa.L=20m，D=0.004m，u=5m/s，作为基准状态，得到的仿真波形如图4所示.

图4 矩形波基准状态仿真图

1)L 分别为20，15，10，5m，得到的仿真结果如图5所示(由于篇幅问题，只列出改变最大得到的仿真图，下同).

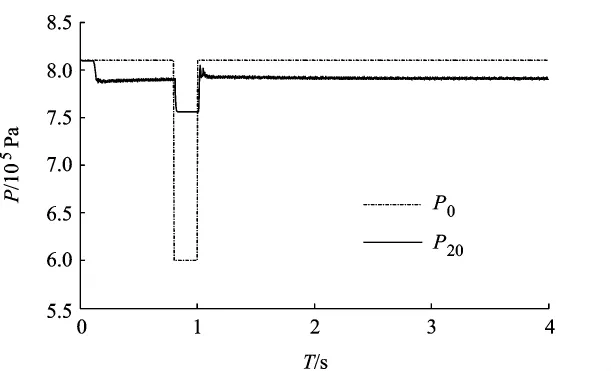
图5 矩形波L=5m仿真图

由仿真结果比较可知，随着空间步长的减小，产生了越来越多的周期性振荡，但对波形的影响不大.

2)D 分别为 0.004，0.009，0.025，0.050，0.100m时，得到的仿真结果如图6所示.

图6 矩形波D=0.100m仿真图

由仿真结果比较可知，随着直径的增大，波形在压力波产生的地方变得很缓和，衰减了压力突变.

3)u 分别为 5，10，15，20，25m/s时，得到的仿真结果如图7所示.

图7 矩形波u=25m/s仿真图

由仿真结果比较可知，改变速度基本上没影响.

4)改变入口压强和下降压强，压降时间仍持续0.2 s.得到的仿真结果如图 8所示.P0=0.4MPa，压降到 0.3MPa.

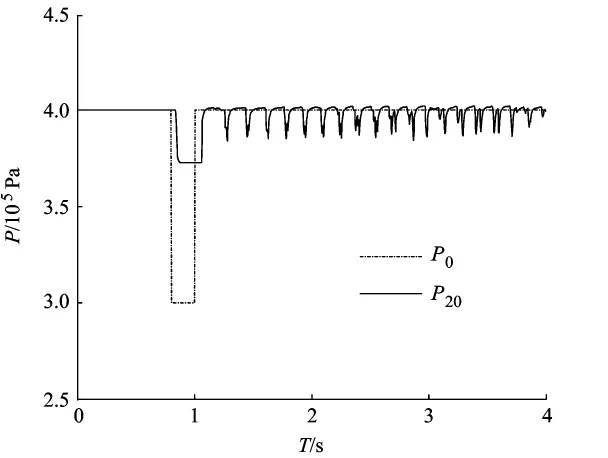
图8 矩形波P0=0.4MPa仿真图

由仿真结果比较可知，改变压强值，增加了毛刺，对波形没有影响.

将以上得到的结论如表1所示.

表1 不同条件对压力波传播影响

3.3 其他波形仿真结果

以三角波、正弦波和下弦波作为输入压力波.由仿真结果可以看出，改变条件对压力波传播的影响跟输入矩形波是一致的.下面只列出基准状态的仿真结果.

1)以三角波为输入压力波，P0=0.81MPa，压强谷值为0.6MPa，压强变化持续0.2 s，再回到0.81MPa.L=20m，D=0.004m，u=5m/s，仿真结果如图9所示.

图9 三角波基准状态仿真图

2)以正弦波为输入压力波，P0=0.81MPa，压强变化持续 0.4 s，振幅为 0.2MPa.L=20m，D=0.004m，u=5m/s，仿真结果如图10 所示.

3)以下弦波为输入压力波，P0=0.81MPa，压强变化持续 0.4 s，振幅为 0.2MPa.L=20m，D=0.004m，u=5m/s，仿真结果如图11 所示.

图10 正弦波基准状态仿真图

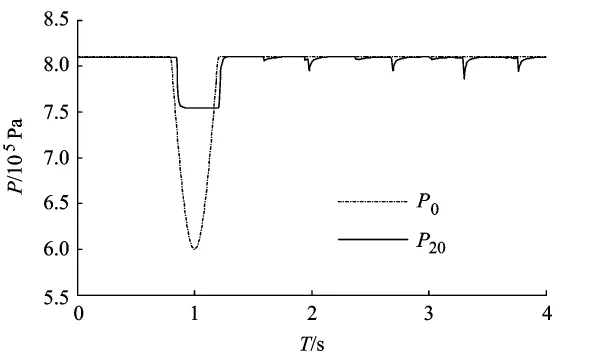
图11 下弦波基准状态仿真图

4 结束语

通过不同波形的压力波在不同的管道条件下的仿真结果，可以得到:管道直径对气体压强传播影响最大;管道长度、压力大小、气流速度也有一定的影响.输入采用正弦波随条件改变而产生比较明显的变化，而下弦波的传输特性比较稳定.矩形波传播过程的相似性最好.因此，利用压力波测流量时，应采用下弦波或矩形波.

做为气体流量的测量，需要较高的精度，对此应对不同的管道做一定的补偿，通过本文的方法，将进一步研究，以获得管道压力波传播的损失系数，用于实际测量的补偿，来实现流量计的精确测量.

References)

［1］黄飞，张西民，郭烈锦.气液两相流中压力波传播的实验研究［J］.自然科学进展，2005，15(4):459 －464 Huang Fei，Zhang Ximin，Guo Liejin.Experimental study of pressure wave propagation in two-phase flow［J］.Progress in Natural Science，2005，15(4):459 －464(in Chinese)

［2］ DeWilde J，Constales D，Heynderickx G J，et al.Assessment of filtered gas-solid momentum transfer models via a linear wave propagation speed test［J］.International Journal of Multiphase Flow，2007，33(6):616 －637

［3］ Xu Xiaoxuan，Gong Jing.A united model for predicting pressure wave speeds in oil and gas two-phase pipeflows［J］.Journal of Petroleum Science and Engineering，2008，60(3/4):150 －160

［4］ Saito S，Iida M，Kajiyama H.Development and verification of numerical simulation of pressure changes in underground high speed railways［J］.RTRI Report，2006，20(1):29 － 34

［5］熊小慧，梁习锋.CRH2型动车组列车交会空气压力波试验分析［J］.铁道学报，2009，31(6):49 －53 Xiong Xiaohui，Liang Xifeng.Analysis of air pressure pulses in meeting of CRH2 EMU trains［J］.Journal of the China Railway Society，2009，31(6):49 －53(in Chinese)

［6］黄亮，苏智勇，蔡茂林.基于压力波传送的管道气体流量测量方法［J］.机床与液压，2008，36(12):138 －140 Huang Liang，Su Zhiyong，Cai Maolin.A new measuring method for gas flow in pipeline based on pressure wave［J］.Machine Tool and Hydraulics，2008，36(12):138 －140(in Chinese)

［7］ Yoshida.Study on dynamic characteristics of gas pipeline system with gas regulator［D］.Tokyo: Tokyo Institute of Technology，2001

［8］蔡茂林.现代气动技术理论与实践第三讲:管路内的气体流动［J］.液压气动与密封，2007，27(4):51 －55 Cai Maolin.Theory and practice of modern pneumatic technology(3):gas flow in pipeline［J］.Hydraulics Pneumatics and Seals，2007，27(4):51 －55(in Chinese)

［9］ Hsieh Po-Wen，Yang Suh-Yuh.Two new upwind difference schemes for a coupled system of convection-diffusion equations arising from the steady MHD duct flow problems［J］.Journal of Computational Phics，2010，229(24):9216 －9234

［10］ Pirozzi M A.High-resolution compact upwind finite difference methods for linear wave phenomena［J］.Applied Numerical Mathematics，2009，59(8):1905 －1921

(编 辑:赵海容)

Analysis on transmitting characteristics of pressure waves in pipeline

Lin Weiqin Huang Liang Cai Maolin

(School of Automation Science and Electrical Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

Based on the theory of one-dimensional unsteady flow，a distributed parameter model of gas transmitting in pipeline was given.Then the model was solved with upwind difference formula，numerical simulations of the transmission of pressure waves in the pipe were also performed.Comparing the result of simulation with experiments，it was verified that this model was correct.And then the initial condition，such as the pipe diameter，air velocity，inlet pressure and the space step of simulation，was changed to simulate the different characteristics of the pipeline.Comparative analysis of the simulation results，the characteristics of the pressure waves of different waveforms under different conditions in the pipeline were obtained.The simulation shows thatwhen using pressure wave to gas flow measure，it should use the waveform of half part of sine or square.

unsteady gas flow;upwind difference;pressure wave;transmit

TH 41

A

1001-5965(2011)05-0600-05

2010-09-27

国家自然科学基金资助项目(50705004);高等学校博士学科点专项科研基金资助项目(20070006041)

林惟锓(1986－)，男，广东潮州人，硕士生，linweiqin2006@163.com.