基于模糊奇偶方程的PL/INS导航系统故障诊断
靳 星 宋 华 邱红专
(北京航空航天大学 自动化科学与电气工程学院,北京 100191)
王养柱
(北京航空航天大学 无人驾驶飞行器设计研究所,北京 100191)
基于模糊奇偶方程的PL/INS导航系统故障诊断
靳 星 宋 华 邱红专
(北京航空航天大学 自动化科学与电气工程学院,北京 100191)
王养柱
(北京航空航天大学 无人驾驶飞行器设计研究所,北京 100191)
提出了一种伪卫星(PL,Pseudolite)/惯性导航(INS,Inertial Navigation System)组合导航系统多故障识别方法.分析了PL的常见故障及其数学模型,采用模糊奇偶方程方法对PL的常见故障进行诊断、隔离和参数识别.采用Takagi-Sugeno(T-S)模糊模型描述PL/INS组合导航系统,对于局部线性化模型建立全解耦奇偶方程,并对奇偶方程的残差进行融合,得到全局残差.结合残差利用卡尔曼滤波进行故障参数识别,给出了参数识别的约束条件.仿真结果表明:针对导航系统中多个PL信号同时发生多种故障的情况,此方法能有效检测故障,并能准确识别出故障模型参数.
伪卫星惯性导航组合导航系统;T-S模糊模型;模糊奇偶方程;多故障诊断
伪卫星(PL,Pseudolite)也被称为陆基发射机或陆基卫星,是一种不在轨道上运行的准导航卫星.具有系统成本低、设置灵活机动、抗干扰性能好等特点,因此,伪卫星技术得到了广泛的关注[1].导航系统的常见故障诊断方法有文献[2]提出的状态χ2检验法和残差χ2检验法,其共同特点是不必分辨造成系统故障的具体原因,而只需实时地确定一个滤波器输出的有效性[3],没有涉及故障的参数识别问题.
全解耦奇偶方程是一种基于解析模型的故障诊断方法,理论上这种方法产生的残差无故障时为零,有故障时非零,且仅对特定故障敏感.利用此残差结合卡尔曼滤波,可识别出故障模型参数,常用于线性系统[4].对于非线性系统,引入Takagi-Sugeno(T-S)模糊模型,结合局部模型的全解耦奇偶方程方法,能够解决非线性系统的故障诊断问题[5].考虑到 PL/INS(Pseudolite/Inertial Navigation System)组合导航系统的非线性和不确定性,本文采用T-S模糊模型描述PL/INS组合导航系统,在此模型基础上,利用全解耦奇偶方程方法对PL故障进行研究,针对全解耦奇偶方程产生的残差,结合Kalman滤波进行故障参数识别.
1 PL/INS的T-S模糊模型描述
1.1 PL/INS组合导航系统误差方程
对于PL/INS组合导航系统,取东北天坐标系为导航坐标系,系统状态方程由惯导系统误差方程和PL的等效误差方程构成,表达式为

其中,x(t)∈R10为系统的状态向量;w(t)为系统噪声向量;G(t)为系统噪声矩阵[6];F(t)为10×10维的矩阵,表达式为

其中,FI(t)为典型的9×9维惯导系统误差矩阵[6];FP(t)=0.
1.2 PL/INS组合导航系统测量方程
PL接收机测量得到的与第k颗伪卫星之间的伪距为
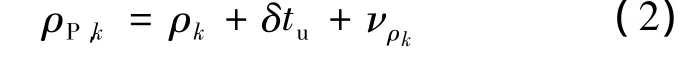
根据飞行器在地理坐标系中的纬度、经度、高度[L,λ,h]以及地理坐标系与地心固连坐标系之间的转换关系,可得到飞行器在地心固连坐标系中的坐标(x,y,z)为

其中,RN为地球半径;f为椭圆扁率.将惯导计算得到的[LI,λI,hI]转换为[xI,yI,zI],再由下式可计算出飞行器与第k颗卫星之间的伪距为
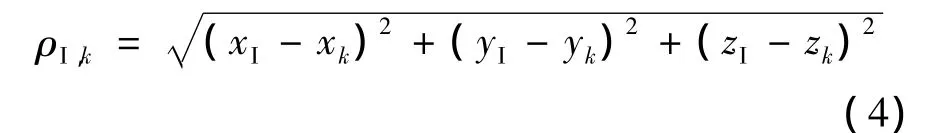
当利用式(2)、式(4)构成的伪距差值作为观测时,观测方程为非线性方程:
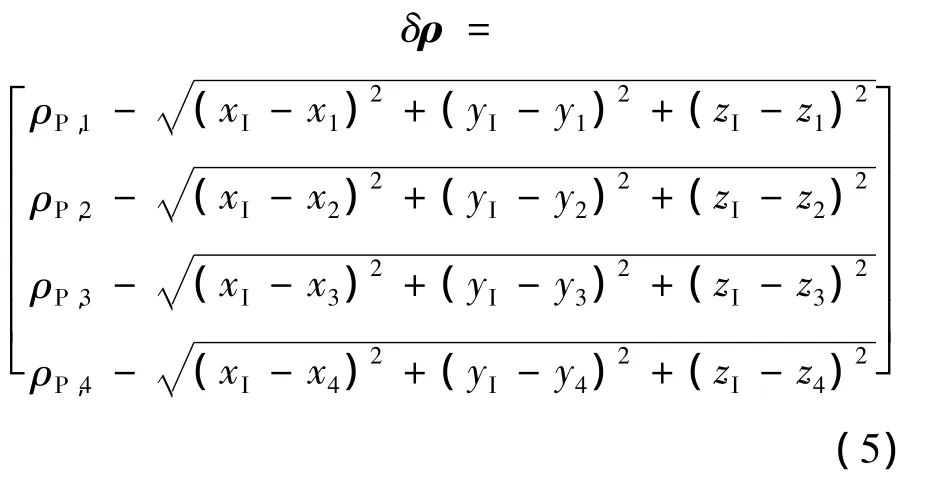
1.3 PL/INS组合导航系统局部线性模型
对于PL/INS组合导航系统,在选定的工作点处进行小偏差线性化即可得到各工作点处的局部线性模型.由式(1)可知,当给定工作点l处的飞行轨迹信息时,组合导航系统的状态方程变为线性方程:
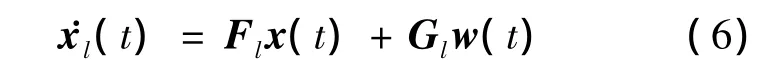
其中,Fl,Gl均为常数矩阵[6].
对于组合导航系统的测量方程,假设[δx,δy,δz]为惯导给出的飞行器在地心固连坐标系中的位置误差,则 xI=x+ δx,yI=y+ δy,zI=z+ δz.将式(4)在[x,y,z]处泰勒展开,并忽略高阶项可得


对于选定的4颗伪卫星可知:

由于导航坐标系采用的是经度、纬度和高度定位的,所以要将[δx,δy,δz]表示成[δλ,δL,δh]的形式.转换关系用T表示,则

与状态方程类似,当给定工作点l处的飞行轨迹信息时,由式(9)、式(10)可得到组合导航系统的线性观测方程为

其中,Hl=[04×6ET K].
由此可得到工作点l处的PL/INS组合导航系统线性模型为

其中,Al,Bl,Cl为 Fl,Gl,Hl离散化之后相对应的矩阵.
1.4 PL/INS的T-S模糊模型描述
由式(1)、式(5)可以看出PL/INS组合导航系统为一个典型的非线性系统;多路径效应、对流层延迟等增加了组合导航系统的不确定性.为了更好地描述系统的非线性和不确定性,本文采用T-S模糊模型对其进行描述.
T-S模糊模型[7]是一种应用局部线性模型描述非线性动态系统的方法.过程为:将非线性系统在各个选定的工作点附近线性化,得到一系列局部线性模型,然后将所有局部线性模型进行加权融合,即可得到描述系统全局性能的T-S模糊模型.
合理选择模糊模型的前件变量ρ,工作点l处的模糊规则可描述如下.
规则 l(l=1,2,…,N):如果 ρ 为 Sl,则导航系统局部线性模型为式(12)所示.其中,Sl为模糊集合;下标l对应非线性系统的第l个工作点以及相应的第l条模糊规则;N为总的规则数.
将以上各规则进行融合即可得到导航系统的全局状态方程和观测方程.由式(1)和式(5)可知,飞行器导航系统的非线性、时变性受飞行器飞行速度、飞行位置以及加速度计输出等因素的影响.因此可选飞行速度(V)、飞行位置(P)和加速度计输出(F)作为前件变量对导航系统进行描述.
这里假设工作点划分为N个,可令

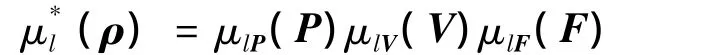
综上,PL/INS组合导航系统的T-S模糊模型为

2 全解耦奇偶方程
2.1 局部模型的全解耦奇偶方程
考虑式(14),将系统噪声向量看作扰动输入,对其工作点l(l=1,2,…,N)处的局部线性模型式(12)建立全解耦奇偶方程[4].
对于数据窗内s+1个最新测量数据y(k-s)至y(k),可得到具有时间冗余的测量方程为

其中,Yl(k)=[yTl(k-s),…,yl(k)T]T为传感器的无故障输出;W(k)=[wT(k-s),…,wT(k)]T为系统噪声向量;ε(k)=[εT(k-s),…,εT(k)]T为测量噪声向量;Hl0,Hlw为具有时间冗余的测量矩阵:

k时刻的奇偶方程为

其中,rl(k)为残差;Zl(k)为与Yl(k)对应的传感器的实际输出;v为奇偶向量,应使奇偶方程产生的残差满足全解耦奇偶方程的条件,即其中,H*=[Hl0Hlw].

当式(18)产生的残差对系统状态解耦、对扰动输入解耦且仅对特定故障敏感时,称式(18)为全解耦奇偶方程[4].
2.2 传感器故障诊断及参数识别
对于工作点l处局部模型的传感器j,具有时间冗余的测量方程为
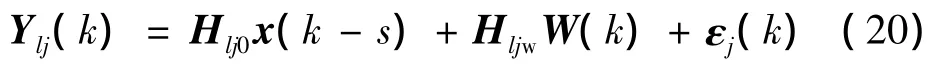
k时刻的全解耦奇偶方程为
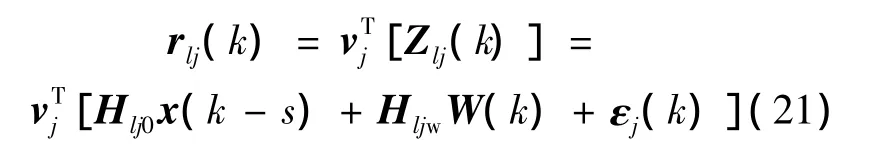
其中,Zlj(k)为与Ylj(k)对应的第j个传感器的实际输出,奇偶向量vj应满足

假设数据窗内同一传感器有相同的故障状态,则传感器j的故障模型可表示为

其中,fj(k)为传感器j的故障模型参数;I为s+1维元素均为1的列向量.将式(20)代入式(23)得
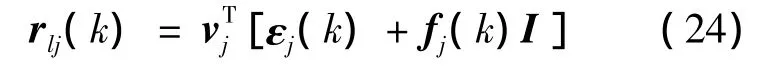
在此基础上,对各个局部线性模型建立全解耦奇偶方程,假设rlj(k)为对工作点l处局部线性模型的第j个传感器建立全解耦奇偶方程产生的残差,则全局奇偶方程的残差可表示为

根据rj(k)可以按下式检测故障:

其中,rt为残差阈值,可由实验数据结合具体系统的可靠性给出.

将故障参数向量表示为随机游走过程:

其中,ζ(k)为高斯随机向量,均值为零,协方差矩阵为Q(k).由式(27)、式(28)利用Kalman滤波可估计出故障参数.需要指出:数据窗长度以及奇偶向量应满足如下约束条件,否则无法对故障参数进行估计.中,v为非零的充分必j要条件为.当 vj不满足约束条件②时,可先验证左零空间中的其它列是否满足,若满足则选取此列作为奇偶向量进行参数估计;否则改变数据窗的长度并重新验证,直至满足以上两约束条件.
3 仿真验证
本节以式(14)所示的PL/INS组合导航系统为例,对模糊奇偶方程的故障诊断方法进行仿真.为简化仿真过程,选定主要参数为:飞行时间为200 s,飞行器沿经线向北加速飞行,初始位置为北纬39°,东经116°,飞行高度为10000m,速度为100~200m/s,PL定位精度10m,数据窗长度s=11.前件变量选为纬度、北向速度和北向加速度计的输出,隶属函数为三角形隶属函数.具体的系统工作点和模糊集隶属函数如图1所示.

图1 前件变量隶属函数
文献[8]列举了GPS/INS组合导航系统的常见故障,并对其进行了建模.考虑到PL与GPS原理的相似性,本文对PL的部分故障利用模糊奇偶方程的方法进行诊断并对故障参数进行辨识.
仿真过程为:按照式(12)对非线性系统在工作点处进行T-S模糊线性化,对每个工作点处的观测量根据式(24)建立全解耦奇偶方程,并由式(25)得到全局奇偶方程的残差进行故障检测,对式(27)、式(28)利用Kalman滤波进行故障识别.下面将对PL的突变性故障和渐变性故障进行诊断和识别.
1)突变型故障.在t>50 s时,假设PL出现突变型故障(时钟跳变、人为干扰等因素引起),导致PL提供的伪距发生改变.故障模型为

其中,fi(i=1,2,3,4)代表各个伪距的故障.
仿真结果如图2、图3所示.图2给出的是发生突变型故障时的各残差值,图3给出的是伪距故障参数估计值的局部放大图.可以看出,发生故障后,各残差发生跳变(跳变之后残差不再为零),说明此方法能有效检测与识别故障.
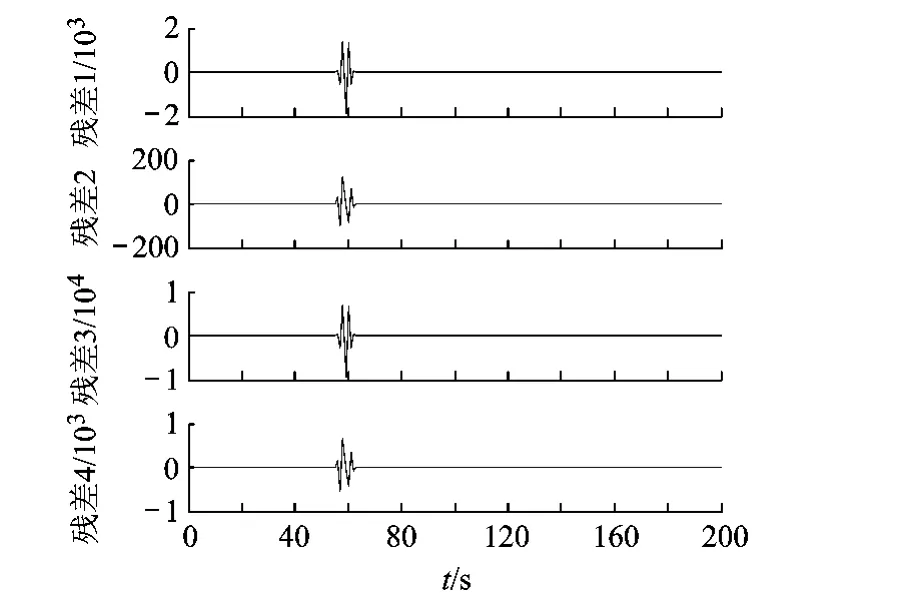
图2 发生突变型故障时的残差

图3 发生突变型故障时故障的估计值(局部放大)
2)渐变型故障.渐变型故障(时钟漂移、可见星数目不足等因素引起)也是PL的常见故障,假设t>30时,PL故障模型为

对于伪距1:a=10m/s,b= -300m.
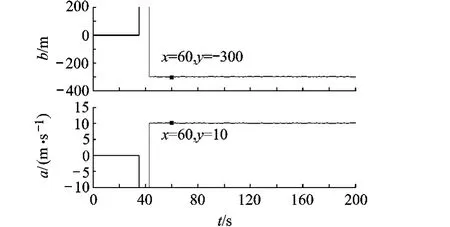
图4 发生渐变型故障时伪距故障的估计值(局部放大)
图4给出了渐变型故障时伪距1故障参数估计值的局部放大图(其它伪距故障与此类似).可以看出该方法能有效检测出渐变型故障并准确识别出故障模型中的斜率和偏差等参数.
4 结论
本文采用T-S模糊模型对PL/INS组合导航系统进行描述.在各个局部线性模型基础上,建立仅对特定传感器敏感的全解耦奇偶方程,然后将各工作点处的局部线性模型的奇偶方程残差进行融合,得到全局奇偶方程的残差,结合Kalman滤波方法,对故障模型参数进行估计.针对PL/INS组合导航系统中PL的常见故障进行了诊断、隔离、参数估计,仿真结果表明,当多个PL信号同时发生多种故障时,此方法也能进行有效地检测和识别.
References)
[1] Bartone C,van Graas F.Ranging airport pseudolite for local area augmentation [J].IEEE Transactions on Aerospace and Electronic Systems2000,36(1):278 -286
[2] Brumaback B D,Srinath M D.A fault-tolerant multisensor navigation system design [J].IEEE Transactions on Aerospace and Electronic Systems,1987,23(6):738 -755
[3] Brumaback B D,Srinath M D.A chi-square test for fault detection in Kalman filters[J].IEEE Transactions on Automatic Control,1987,32(6):552 -554
[4] Song Hua,Zhang Hongyue.An approach to sensor fault diagnosis based on fully-decoupled parity equation and parameter estimate[C]//Yugeng X,Xiren C,Lei G.Proceedings of the 4th World Congress on Intelligent Control and Automation.Shanghai:Press of East China University of Science and Technology,2002:2750-2754
[5]宋华,张洪钺.模糊非线性奇偶方程故障诊断方法[J].自动化学报,2003,29(6):965 -970 Song Hua,Zhang Hongyue.Fault diagnostic method for nonlinear system based on fuzzy parity equation [J].Automatic,2003,29(6):965-970(in Chinese)
[6]袁信,余济祥,陈哲.导航系统[M].北京:航空工业出版社,1993:190-193 Yuan Xin,Yu Jixiang,Chen Zhe.Navigation system[M].Beijing:Aviation Industry Press,1993:190 -193(in Chinese)
[7] Takagi T,SugenoM.Fuzzy identification of systems and its application to modeling and control[J].IEEE Trans on Systems,Man,and Cybernatics,1985,15(1):116 -132
[8] Umar IB,Washington Y O.Failure modes and models for integrated GPS/INS systems[J].The Journal of Navigation,2007,60:327-348
(编 辑:刘登敏)
Fuzzy parity equation based fault diagnosis approach for PL/INS navigation system
Jin Xing Song Hua Qiu Hongzhuan
(School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Wang Yangzhu
(Research Institute of Unmanned Aerial Vehicle,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
A method for multiple faults identification for pseudolite(PL)/inertial navigation system(INS)tightly coupled navigation system was presented.The failures associated with PL and their modes were analyzed,what is more,fuzzy parity equations were used to identify the PL failure modes.First of all,the PL/INS tightly coupled navigation system was described by a Takagi-Sugeno(T-S)fuzzy model,and then the full de-coupled parity equations were applied to the local linear models.The faults can be detected by the sum of the local residuals and Kalman filter algorithm was used for identifying the parameters of failure modes.Besides,the necessary conditions for parameter identification were given.The simulation results show that,in case of multiple signal faults and multiple types of fault in PL simultaneously,thismethod can effectively detect them and precisely identify the parameters of failure modes.
pseudolite/inertial navigation system coupled navigation system;T-S fuzzy model;fuzzy parity equation;multiple faults diagnosis
TP 206+.3
A
1001-5965(2011)06-0748-05
2010-03-16
靳 星(1984-),男,河北文安人,硕士生,jinxingbuaa@gmail.com.

