基于非饱和渗流应力耦合的河堤窝崩机理

罗玉龙，张文捷，速宝玉，盛金昌

(1.河海大学水利水电学院，江苏南京 210098;2.江西省水利厅，江西南昌 330009)

河堤窝崩的破坏性巨大，发生频繁，如1996年江西彭泽马湖堤窝崩和1998年湖北长江干堤石首段窝崩均造成了十分巨大的损失.研究窝崩机理，探讨窝崩形成原因和规律，提高窝崩预报的准确性，为工程治理措施提供科学依据，是防洪减灾和河道治理领域迫切需要解决的课题，具有重大的理论和现实意义.

国内外诸多学者从土坡稳定[1-2]、河流动力学[3-4]、液化[5]角度等研究窝崩，张幸农等[6-7]详细总结了该课题的研究进展，这些均为窝崩的预防、治理提供了理论依据.其中，基于土坡稳定角度的研究，经历了从无黏性岸坡[8]到黏性岸坡[9]，从干燥[10]到饱和再到非饱和状态[11-12]的演变过程.随着分析方法的不断完善，各种可能导致窝崩的因素逐渐被考虑，如孔隙水压力、基质吸力、静水压力、植被、外河水位的变化等，但是现有的窝崩分析方法仍然存在以下不足:(a)岸坡典型截面比较理想，简单;(b)只能考虑均质的或层状组成的岸坡; (c)孔隙水压力及基质吸力的分布考虑比较粗糙;(d)一般仅适用于较陡(坡角大于60度)的黏性岸坡，要将上述方法应用到实际窝崩的预测尚需要进一步的简化.因此，亟待研究更加一般实用的窝崩分析模型或方法.

本文根据长江流域九江段堤防地质地形特征建立简化的河堤窝崩模型，从土坡稳定的角度出发，根据强度折减原理，采用饱和非饱和渗流应力耦合方法，综合分析岸坡内在因素和外界动力因素对窝崩形成的作用，进一步探讨窝崩的机理.

1 非饱和渗流应力耦合基本理论

窝崩的本质就是水土的渗流应力耦合作用，其基本控制方程包括平衡方程、渗流连续性方程、土体本构方程、有效应力原理等.通过对时间和空间的离散，得到如下基本控制方程[13]平衡方程

式中:K——单元劲度矩阵;Δδ——节点位移增量;Ld——单元耦合矩阵;uw，Δuw——节点孔隙水压力及增量;ΔF——外部节点力增量;Lf——渗流耦合矩阵;Kf——单元刚度矩阵;MN——质量矩阵;Q——边界节点的流量;B——应变矩阵;D——非饱和土体的本构矩阵;N——形函数的行向量;Kw——渗透系数矩阵; E——土体的弹性模量;H——基质吸力引起的非饱和土结构模量;ν——泊松比;Δt——时间增量;ρw——水的密度;R——土水特征曲线的斜率的导数.

土体的本构模型采用理想弹塑性模型，屈服准则为Mohr-Coulomb准则.关于流动法则的选取，已有研究表明，流动法则对于岸坡整体安全系数的精度影响很小，因此，本文采用关联流动法则，根据上述基本理论和强度折减原理，建立计算河堤窝崩的有限元模型研究窝崩机理.

2 窝崩的影响因素分析

2.1 河堤窝崩的概化模型

导致窝崩的主要因素有:岸坡土体地质因素(黏聚力、内摩擦角等)，地形因素(岸坡坡比等)，河流动力因素(河流侵蚀坡脚)及水文地质因素(岸坡内外水位差)等，本文以长江流域九江段堤防地质地形特征为背景，提出如图1所示的概化模型:均质堤防高7m，坡比1∶3，岸滩高8m，坡比1∶2，土体干密度1.7t/m3，变形模量为20.0MPa，泊松比0.3，黏聚力12.90kPa，内摩擦角17.9°.土体饱和渗透系数为2.0×10-8m/s，非饱和渗透参数见文献[14].

边界条件:底边不透水边界，水平、竖向位移均约束;岸坡表面为可能出逸边界，左右两侧竖向边界水平位移约束，岸坡内外水位以下边界为已知水头边界.岸坡失稳判据目前尚无统一标准，本文采用收敛性准则结合特征点位移突变准则作为失稳判据.具体做法:首先试算一个较小的安全系数Fs以保证计算收敛，岸坡处于初始稳定状态，随后逐渐增大安全系数，并观测特征点位移变化(取堤顶 A点作为观测点)，直至计算不再收敛，特征点位移发生突变，此时安全系数即为最小安全系数Fmin.

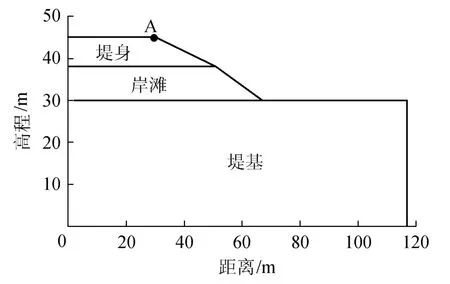
图1 河堤窝崩概化模型Fig.1 Generalized model for arc collapse of riverbanks

图2 非耦合情况临界状态的等效塑性应变Fig.2 Equivalent plastic strain in critical state of uncoupling case

2.2 非耦合情况

为了说明渗流应力耦合分析的必要性，本节不考虑渗流应力耦合作用，首先计算渗流场，然后将渗透力作为体积力荷载施加，进行应力分析，以考察耦合分析和非耦合分析的差异.取土体黏聚力为12.90 kPa，内摩擦角为17.90°，岸坡内外水位差为7m的情况进行非耦合分析.分析结果表明，不考虑耦合的情况下，岸坡开始滑动时的最小安全系数为1.35，其潜在的最危险滑动面(图中粗线)如图2所示.

由后续耦合分析可知，相同条件下，考虑渗流应力耦合作用的情况，其最小安全系数仅为1.25，比非耦合情况小0.1，差别明显.由此可见，在研究窝崩时，考虑非饱和渗流应力耦合作用十分必要.

2.3 非饱和渗流应力耦合情况

为了在工程有效范围内比较各影响因素的敏感性，假设概化模型为Ⅱ级堤防，根据GB50286—98《堤防工程设计规范》，Ⅱ级堤防正常运用条件允许的最小安全系数为1.25，因此，设定安全系数的变化范围均在1.05～1.25之间.

2.3.1 岸坡土体黏聚力的影响

保持岸坡几何形态及其他土体力学指标不变，仅改变黏聚力，分别考察黏聚力c为6.55kPa，7.51kPa，9.09kPa，11.57kPa，12.90kPa等5种情况的岸坡稳定性.黏聚力为12.90kPa时等效塑性应变、位移等值线如图3和图4所示，黏聚力与最小安全系数的关系如图5所示.

从图3和图4及其他情况的等值线可以看出，对于同一黏聚力而言，随着安全系数的增大，塑性区的范围和等效塑性应变的值都逐渐增大，直至塑性区贯通，岸坡具有明显的圆弧滑动趋势，岸坡发生破坏.对于不同黏聚力，黏聚力越大，越有利于岸坡的稳定，发生破坏的最小安全系数越大，破坏时的最大等效塑性应变越小.位移分布特点:黏聚力越大，坡体位移越小，其中位移最大的位置是A点附近的坡顶.

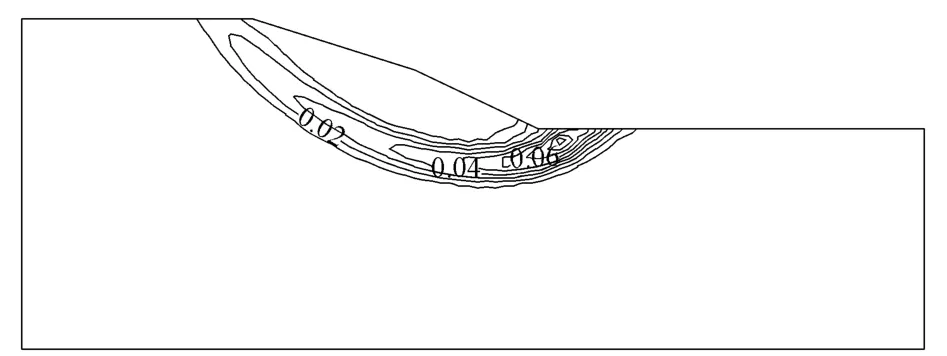
图3 临界状态等效塑性应变(c=12.90kPa)Fig.3 Equivalent plastic strain in critical state(c=12.90kPa)

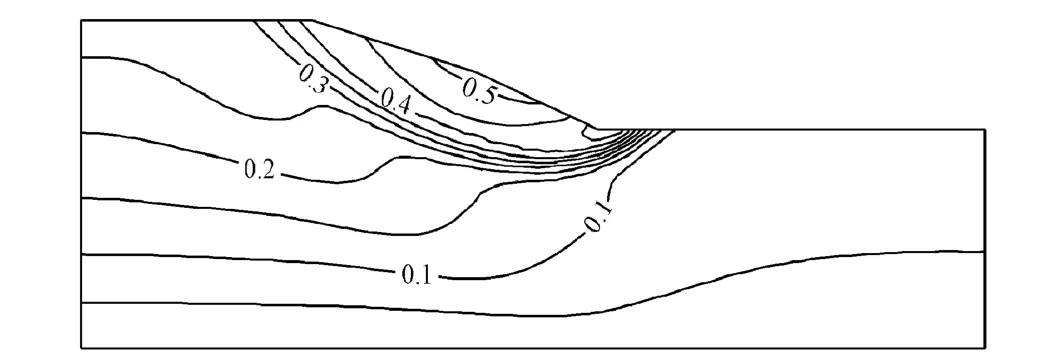
图4 位移等值线(c=12.90kPa，Fs=1.25，单位:m)Fig.4 Displacement contours(c=12.90 kPa，Fs=1.25，unit:m)

由图5可见，黏聚力与最小安全系数的关系具有近似的线性特征，黏聚力越大，最小安全系数越大，越有利于岸坡的稳定.

2.3.2 岸坡土体内摩擦角的影响

分别考察内摩擦角φ为14.36°，15.23°，16.11°，17.13°，17.90°等5种情况岸坡的稳定性.内摩擦角与最小安全系数的关系如图6所示.

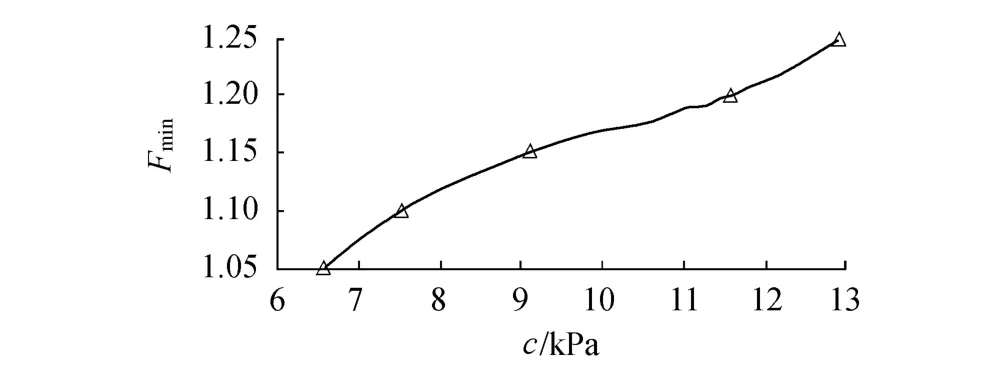
图5 最小安全系数与黏聚力关系Fig.5 Relationship between Fminand cohesion

图6 最小安全系数与内摩擦角关系Fig.6 Relationship between Fminand friction angle

从图6可见，内摩擦角与最小安全系数的关系具有明显的线性特征，内摩擦角越大，最小安全系数越大，越有利于岸坡的稳定.

综上研究表明，黏聚力和内摩擦角是防止窝崩的有利因素，两者越大，越有利于岸坡的稳定，岸坡的最小安全系数越大.

2.3.3 岸坡坡比的影响

仅改变岸坡坡比，考察岸坡坡比分别为1∶2.00(坡角26.57°)，1∶1.50(坡角33.69°)，1∶1.00(坡角45°)，1∶0.85(坡角49.64°)，1∶0.75(坡角53.13°)时对岸坡稳定性的影响.坡比为1∶0.85时等效塑性应变分布如图7所示，岸坡坡角与最小安全系数的关系如图8所示.

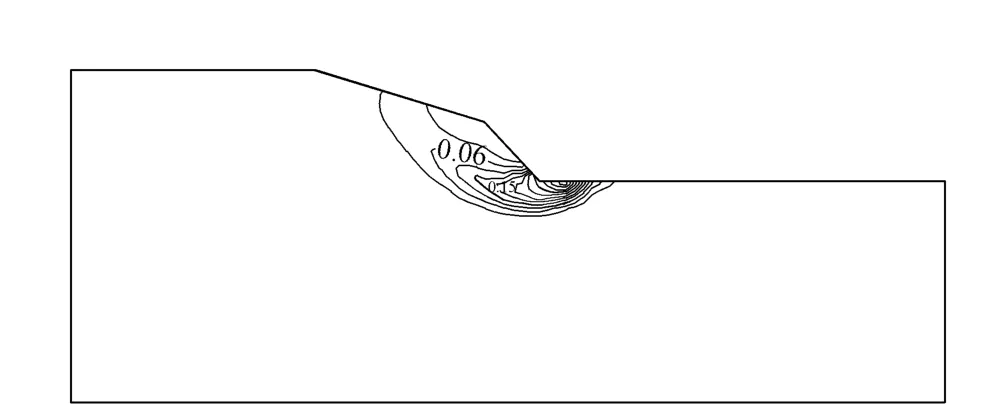
图7 岸坡坡比1∶0.85时临界状态等效塑性应变Fig.7 Equivalent plastic strain in critical state at slope ratio of 1∶0.85

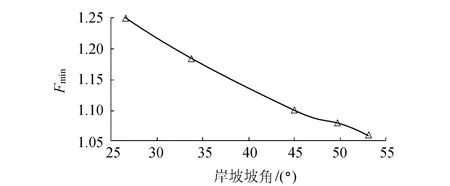
图8 最小安全系数与岸坡坡角关系Fig.8 Relationship between Fminand slope angle

由图7可以看出，岸坡坡比对岸坡的破坏形式具有重要影响.对于岸坡较陡的情况，从岸滩滩脚开始逐渐形成到堤坡中部贯通的塑性破坏区，位移也呈现明显的圆弧滑裂面形状，岸坡主要发生破坏范围较小的局部滑动.而对于岸坡较平缓的情况，则形成从岸滩滩脚到河堤顶部贯通的塑性破坏区，岸坡主要发生整体滑动，破坏的土体体积更大.可见，岸坡角度越大，岸坡越容易失稳，坡角越小，岸坡越稳定.

2.3.4 河流动力因素的影响

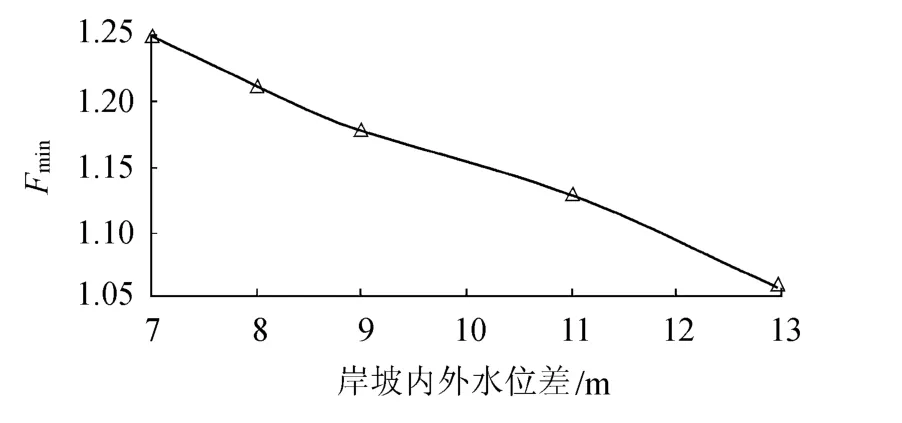
图9 最小安全系数与岸坡内外水位差关系Fig.9 Relationship between Fminand water level difference

河流动力因素是诱发窝崩的另一重要因素，其对窝崩的影响主要表现为:(a)河道纵向水流形成的贴岸冲刷及其顶冲作用，不断地冲蚀淘空岸脚;(b)横向环流、竖向回流等形成的岸边淘刷.由于河流动力因素对窝崩影响非常复杂，其引起的岸坡及岸滩滩脚的侵蚀很难量化，但是，从本质上说，河流侵蚀岸滩滩脚就是间接地增大岸坡的坡角，因此，将河流动力因素近似地认为与岸坡坡比对窝崩的影响程度一致.

2.3.5 岸坡内外水位差的影响

岸坡外水位高程始终为30m，仅改变岸坡内水位，考察岸坡内外水位差分别为7～13m时岸坡的最小安全系数.岸坡内外水位差与最小安全系数的关系如图9所示.

由图9可见，岸坡内外水位差与最小安全系数的关系具有明显的线性特征，岸坡内外水位差越大，越不利于岸坡稳定，岸坡的最小安全系数越小.

3 敏感性分析

敏感度是指当一个自变量发生变化时所引起的因变量的改变率.窝崩影响因素的敏感性分析主要是研究影响窝崩的各因素与相应的安全系数之间的相互关系，进而确定各因素对窝崩的贡献大小.它通过各因素的相对变化率与安全系数的相对变化率之间的比值进行衡量，即第i个影响因素的敏感度Si可表示为

式中:ΔXi——第i个影响因素的变化量;Ximax-Ximin——第i个影响因素的最大变化量;ΔFSi——第i个影响因素对应的安全系数FSi对应ΔXi的变化量，FS0为 FSi的基准值.本文选取黏聚力12.90 kPa，内摩擦角17.90°，岸滩坡比1∶2.00，岸坡内外水位差为7m的情况作为标准情况，其对应的最小安全系数1.25即为FS0，根据公式(3)～(5)分别计算各因素的敏感度.计算结果表明，黏聚力、内摩擦角、岸坡坡比(或河流动力因素)、岸坡内外水位差等因素对窝崩的敏感度顺序从大到小为岸坡坡比(或河流动力因素)、黏聚力、内摩擦角、岸坡内外水位差，即岸坡坡比(或河流动力因素)是诱发窝崩的控制性因素.

4 结 论

a.窝崩的本质是岸坡土体在各种不利因素的组合或某个单一不利因素很强烈地作用下发生剪切破坏所致.具体来说，黏聚力、内摩擦角通过减小土体抗剪强度使土体发生剪切破坏;岸坡坡角通过增大下滑力使土体发生剪切破坏而滑动;岸脚侵蚀则是通过逐年冲刷侵蚀下切，使岸坡的坡角、坡高变大来诱发窝崩;岸坡内外水位差通过减小黏聚力、内摩擦角等抗剪强度指标，增大渗流出口的渗透坡降，增大对稳定不利的渗透力等多种方式使岸坡破坏.

b.黏聚力及内摩擦角是防止窝崩的有利因素，两者越大，岸坡越稳定;而岸坡坡角、岸坡内外水位差、河流侵蚀等是诱发窝崩的不利因素，其数值越大，不利因素越聚集，岸坡越不稳定.

c.岸坡坡比是防止窝崩的控制性因素.岸坡坡角大于临界坡角，发生窝崩的可能性较大，这为岸坡检查加固、简化窝崩监测、建立防止岸坡坡角变大的新型护岸固脚技术提供了基本的理论依据.

d.通过与非耦合情况的比较可以发现，采用非饱和渗流应力耦合有限元法研究窝崩是十分必要的，该法弥补了传统窝崩分析方法在研究岸坡截面简单、孔隙水压力及基质吸力考虑比较粗糙等方面的缺陷.

[1]RINALDI M，CASAGLI N.Stability of streambanks formed in partially saturated soilsand effects of negative pore water pressure:the Sieve River(Italy)[J].Geomorphology，1999，26(4):253-277.

[2]黄本胜，白玉川，万艳春.河岸崩塌机理的理论模式及其计算[J].水利学报，2002，33(9):49-60.(HUANG Ben-sheng，BAI Yuchuan，WAN Yan-chun.Model for dilapidation mechanism of riverbank[J].Journal of Hydraulic Engineering，2002，33(9):49-60.(in Chinese))

[3]LUPPI L，RINALDI M，TERUGGI L B，et al.Monitoring and numerical modeling of riverbank erosion processes:a case study along the Cecina River(Central Italy)[J].Earth Surface Processes and Landforms，2009，34(4):530-546.

[4]张幸农，应强，陈长英，等.江河崩岸的概化模拟试验研究[J].水利学报，2009，40(3):263-267.(ZHANG Xing-nong，YING Qiang，CHEN Chang-ying，et al.Generalized model study on mechanism of riverbank failure[J].Journal of Hydraulic Engineering，2009，40(3):263-267.(in Chinese))

[5]WANG F，SHIBATA H.Influence of soil permeability on rainfall-induced flowslides in laboratory flume tests[J].Canadian Geotechnical Journal，2007，44(9):1128-1136.

[6]张幸农，蒋传丰，应强，等.江河崩岸问题研究—综述[J].水利水电科技进展，2008，28(3):80-83.(ZHANG Xing-nong，JANG Chuang-feng，YING Qiang，et al.Review of research on bank collapse in natural rivers[J].Advances in Science and Technology of Water Resources，2008，28(3):80-83.(in Chinese))

[7]张幸农，蒋传丰，陈长英，等.江河崩岸的类型与特征[J].水利水电科技进展，2008，28(5):66-70.(ZHANG Xing-nong，JIANG Chuan-feng，CHEN Chang-ying，et al.Types and features of riverbank collapse[J].Advances in Science and Technology of Water Resources，2008，28(5):66-70.(in Chinese))

[8]KOVACS A，PAR KER G.A new vectorial bedload formulation and its application to the time evolution of straight river channels[J]. Journal of Fluid Mechanics，1994，267:153-183.

[9]DAPPORTO S，RINALDI M，CASAGLI N，et al.Mechanisms of riverbank failure along the Arno River，Central Italy[J].Earth Surface Processes and Landforms，2003，28(12):1303-1323.

[10]THOR NE C R，TOVEY N K.Stability of composite river banks[J].Earth Surface Processes and Landforms，1981，6(5):469-484.

[11]RINALDI M，CASAGLI N，DAPPORTO S，et al.Monitoring and modeling of pore water pressure changes and riverbank stability during flow events[J].Earth Surface Processes and Landforms，2004，29(2):237-254.

[12]SHIELDS J，DOUGLAS F，SIMON A，et al.Streambank dewatering for increased stability[J].Hydrological Processes，2009，23(11):1537 -1547.

[13]廖红建，王铁行.岩土工程数值分析[M].北京:机械工业出版社，2006:106-110.

[14]彭华，陈尚法，陈胜宏.水布垭大岩淌滑坡非饱和渗流分析与渗控优化[J].岩石力学与工程学报，2002，21(7):1027-1033. (PENG Hua，CHEN Shang-fa，CHEN Sheng-hong.Analysis on unsaturated seepage and optimization of seepage control for Dayantan landslide in Shuibuya Project[J].Chinese Journal of Rock Mechanics and Engineering，2002，21(7):1027-1033.(in Chinese))