螺旋电感品质因数Q的GP优化

李美娇，严梦霄，荣溢炯

（1.浙江大学 信息与电子工程学系，浙江 杭州 310058；2.劳伦斯技术大学 电机学院，密西根州 绍斯菲尔德 48075）

如今的电子技术正朝着小型化，智能化，集成化方向发展。电感的集成就是其中重要的一环[1-2]。电感集成不仅能使电路小型化，还可通过减少与外界的连线，来避免了寄生参数的影响，从而防止了由连线引入的电磁干扰，也可进一步提高射频级的性能。电感集成的难点就在于如何能在较高的频率上，在较小的面积内制作出并有足够高的Q值且尽可能大的电感。

品质因数Q是表征无源器件质量的一个重要参数。Q为感抗XL与其等效电阻的比值。Q越高，回路损耗越小，其振荡信号越稳定。集成螺旋电感的损耗大致来源于3个方面：一是金属线的电阻；二是电感面和衬底间的寄生电容将电感中的一部分能量耦合到衬底消耗了；三是电感中的电流所产生的磁场将一部分能量耦合到衬底中形成电流消耗了[3]。由于损耗太大，集成电感的Q值都很低。本文详细分析了集成电路螺旋电感的一种物理模型。通过matlab仿真，得出了金属线宽和线间距对螺旋电感品质因数的影响。在此基础上对螺旋电感模型整体进行了严格的GP优化，实现了在对确定的电感值及其他设计要求不变的前提下螺旋电感品质因数Q的优化。采用优化结果进行设计，可以使品质因数Q得到明显提高。

1 螺旋电感物理模型分析

图1 矩形平面螺旋电感Fig.1 Square inductor

随着技术发展，电感正由三维向平面化发展，目前常用的集成电感是平面螺旋电感（spiral inductors），如图1所示[4]。螺旋线的形状一般是矩形的，也可以做成六边形，八边形（图2，3）或圆形，圆形螺旋电感在给定的金属线宽度和电感值下电阻损耗最小，Q值也最高，但生产技术难以实现。

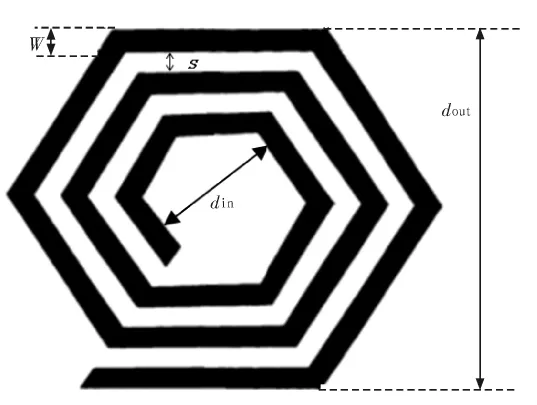
图2 六边形平面螺旋电感Fig.2 Hexagonal inductor

图3 八边形平面螺旋电感Fig.3 Octagonal inductor

定义螺旋电感的外径 dout，内径din，金属线宽W，线间距s（图 1，2，3所示）和匝数 n，得到螺旋电感的平均直径 davg，线长度l，面积A的计算公式：

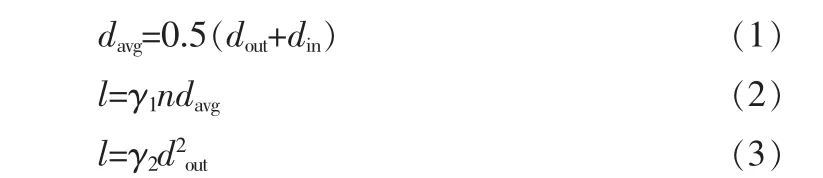
其中，γ1、γ2为系数，其取值如表 1 所示。

表1 矩形、六边形、八边形参数Tab.1 Parameters of square， hexagonal， octagonal

图4所示为螺旋电感的物理模型[5]，其中Ls和Rs是串联电感和电阻，Cs是导体间的电容，Cox是电感与硅衬底间的电容，CSi和RSi表示硅衬底的电容和电阻。

各参数的公式如下：

图4 硅衬底螺旋电感物理模型Fig.4 Circuit model of sillicon base spiral inductor

其中 α1～α5的数值见表 2。

表2 矩形、六边形、八边形对应参数数值Tab.2 Parameters of square， hexagonal， octagonal

其中，εox=3.451 0－13F/cm，k2= εox/（2tox）。

为便于优化将图4的模型转化为图5所示的模型。

图5 硅衬底螺旋电感物理模型简化图Fig.5 Simplified circuit model of sillicon base spiral inductor

其中，

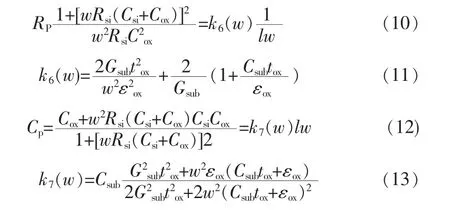
品质因数Q的表达式：

2 单变量对Q值的影响

通过设定参数 n，W，dout的数值，以 s（线间距）为变量，通过matlab仿真可以得到Q值随s的变化关系；同样通过设定参数 n，s，dout的数值，以 W（金属线宽）为变量，通过 matlab仿真可以得到Q值随W的变化关系如图6所示。

从图中观察得到Q随s的增加而减少，Q随W的增加而先增加后降低。可以看出单变量对Q值得影响是不同的，因此存在一个最优化问题。所以希望找到一种方式可以在一定的限制条件下，变化与Q值有关的多个变量，找到在电感值及其他限定条件不变的情况下，Q的最大值及Q值的优化，研究发现GP优化可以很好地完成此项工作。

图6 单变量s，W对Q值的影响Fig.6 Q-s and Q-W curves

3 GP优化简介

GP 可以对单项式（如 g（x））和多项式（如 f（x））进行优化，要求系数 c（或 ck）为整数。

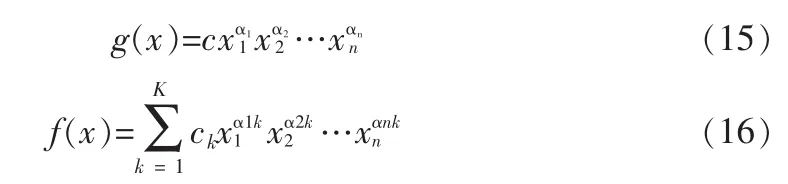
优化形式如下：可以求出在限定条件下fo的最大值或最小值。要求限定条件为关于单项式或多项式的不等式或等式，其中不等式左边可以是单项式或多项式，而不等式右边只能是单项式。

Minimize f0（x）

Subject to fi（x）≤1,i=1,…，m

gi（x）=1，i=1,…，p

GP优化的关键函数：

gpvar定义变量

constr设定限制条件

[opt_val sol status]=gpsolve（QL， constr， ’max’）优化命令。

该式子将求得QL在constr的限定条件下的max（最大值）（求最小值可将max改为min），并将得到QL的优化值赋给opt_val。

可见，只要能将优化目标与变量的关系式化为多项式形式，变量的限制条件化为符合GP要求的单项式或多项式形式，就可以采用GP优化形式对目标进行优化。

4 品质因数Q的GP优化

通过对Qmin≤Q，进行化简得到Qmin，即目标函数限定关系

式如下[1]：

其他的限定条件范围及常数设定如下式及表3所示：

Ls=L，Ls,min≤Ls≤Ls,max，W≥Wmin， s ≥smin,d2out≤Areamax,，davg+ns+nW≤dout

表3 程序中变量范围设置Tab.3 Variables range setting in program

另外需要用到，Csub和Gsub分别代表硅衬底单位面积的电容和电导。在本文中，采用电阻率为10 Ωcm的硅衬底，Csub和Gsub分别 1.6×10－6F/m2和 4×104S/m2。

设定电感值的变化范围为2～20 nH，得到1.6 GHz下对应的Q值优化曲线，如图7所示。

图7 1.6 GHz时矩形平面螺旋电感Q值随L变化的优化曲线（8 nH处Qmax为6.6升）Fig.7 Q-L curve of square inductor，while f=1.6 GHz（Qmax=6.641， when L=8nH）

5 GP优化方法的优势

应用遗传算法设计一个工作在1.6 GHz，电感值为8 nH的方形平面螺旋电感，得到的最佳设计方案为，dout=344 μm，导线宽度W=12.2 μm，导线间隔S=3.2 μm，Q值最优解为5.8[6];而查询等Q值线所得到的工作在1.6 GHz，电感值为8 nH的方形平面螺旋电感Q值最优解为5.3。应用GP优化得到的矩形螺旋电感面积不大于 400 μm2，Q值最优解为6.641，与遗传算法相比提高了14.5%，与等Q值线相比提高了20.2%，可以看出，方形螺旋电感品质因数是大大优化了。

6 不同形状的螺旋电感Qmax随L变化曲线

根据表2的参数，更改程序，得到图8、图9。

图8 1.6 GHz时六边形平面螺旋电感Q值随L变化的优化曲线（8 nH 处 Qmax为 6.649）Fig.8 Q-L curve of hexagonal inductor，while f=1.6GHz（Qmax=6.649， when L=8nH）

图9 1.6 GHz时八边形平面螺旋电感Q值随L变化的优化曲线（8 nH 处 Qmax为 6.638）Fig.9 Q-L curve of octagonal inductor，while f=1.6GHz（Qmax=6.638， whenL=8nH）

由图可见，在相同工艺参数及限制条件下，随着螺旋电感边数的增多，同数值的电感所得到的Qmax变化并不大。

7 结论

本文有3点创新之处。首先，为了利用GP优化的方法研究螺旋电感品质因数Q的特性，需要进行建模；而建模所需的变量并不是如同其他仿真实验一样根据经验直接设定，而是通过另一个单独的程序来研究究竟哪些因素对Q的影响比较大，会有怎样的制约关系，通过matlab仿真，得到了Q随s，W变化的曲线图，进而确定了s，W作为建模的主要变量；其次，在对螺旋电感进行GP优化时，并不是单纯地研究四边形电感的品质因数最大值，而是拓展到六边形、八边形，比较了3种螺旋电感在相同实验条件设定的前提下Qmax的不同；最后，在分析GP优化方法的同时，还将它与其他螺旋电感品质因数优化的方法进行了比较，发现GP优化较一般线性规划、查表法等方法有快捷精确的优势，在相同条件下，Q值分别提高了14.5%和20.2%，得到其他方法所不能企及的最优解。

[1] Niknejad A M，Meyer R G.Analysis，design，and optimization of spiral inductors and transformers for Si RF ICs[J]IEEE Journal of Solid-State Circuits， 1998，33（10）：1470-1481.

[2] Yue C P，Wong S S.On-chip spiral inductors with patterned ground shields for Si-based RF ICs[J].IEEE Journal of Solid-State Circuits， 1998，33（5）：743-752.

[3] 陈邦媛.射频通信电路[M].2版.北京:科技出版社，2006.

[4] Del Mar Hershenson M.CMOS analog circuit design via geometric programming[C]//American Control Conference，2004（4）：3266-3271.

[5] Yue C P，Wong S S.Physical modeling of spiral inductors on silicon[J].IEEE Transactions on Electron Devices， 2000，47（3）：560-568.

[6] 林敏，李永明，陈弘毅.一种基于物理模型与遗传算法的平面螺旋电感技术[J].半导体学报， 2001， 22（7）：897-903.LIN Min， LI Yong-ming， CHEN Hong-yi.An optimization technique for planar spiral inductor based on the inductor’s physicalmodeland genetic algorithm [J].Journalof Semiconductors， 2001， 22（7）:897-903.