多边形链的完美匹配数与Caterpillar树的Hosoya指标之间关系

杨 秀，赵 飚

（新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830046）

1 引言

1971年，日本化学家Hosoya[1]首次提出一种拓扑指标，用Z来表示.后人称之为Hosoya指标，它是研究苯碳氢化合物的分子结构与其物理化学性质之间联系的一类重要参数,并且他证明了该指标与苯碳氢化合物的物理化学性质,尤其是与它的沸点有紧密联系.

设G（E，V）是一个化学图,则图G的Hosoya指标定义为G的所有匹配的数目之和，记作Z（G）,即

其中，m(G,k)为图G中含有k条边的匹配的数目.为计算方便，我们规定m(G,0)=1.

我们先回顾一些基本概念，六边形系统是一个有限的2-连通平面图，并且它的每一个内部面都为六边形；六边形链是这样一个六边形系统，它的每一个六边形都至多有两个相邻的六边形.

同样的，八边形系统是一个有限的2-连通平面图，并且它的每一个内部面都为八边形；八边形链是这样一个八边形系统，它的每一个八边形都至多有两个相邻的八边形，如图1所示.

称M哿E(G)是G的匹配,如果M中的任意两条边在G中都不相邻.称M是G的完美匹配,如果V(M)=V(G).本文中的Kekulé 结构也就是图论中所定义的完美匹配.

近年来，关于六边形链的Hosoya指标已有许多重要结果.Gutman[2]证明了在所有六边形链中，直六边形链是具有极小Hosoya指标的唯一六边形链；张.[3]证明了Zig-zag六边形链是具有极大Hosoya指标的唯一六边形链；Gutman[4]证明了六边形链的六边形多项式BG(X)与Caterpillar树的特征多项式之间有紧密联系，作为一个推论推出，存在一类Caterpillar树使得六边形链的Kekulé 结构的数目与Caterpillar树的Hosoya指标相等；沿这条主线，Hosoya和Gutman[5]研究了六边形链的Kekulé 结构数目与一些看似无关的概念之间的联系，如路的匹配数，同时也给出了六边形链H的Kekulé 结构数目的具体表达公式；2012年，李树立[6]证明了存在与四边形链相对应的Caterpillar树使得它的Hosoya指标与四边形链的Kekulé 结构数目相等.本文作者在上一篇文章中证明了存在与八边形链相对应的Caterpillar树使得它的Hosoya指标与八边形链的Kekulé 结构数目相等.

在这篇文章中，主要通过一种新的变换方法，证明对于任意八边形链存在与之相对应的Caterpillar树，使得Caterpillar树的Hosoya指标与八边形链的Kekulé 结构数目相等，并给出Kekulé 结构数目的表达公式.

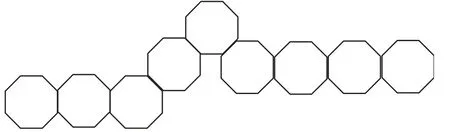
图1

2 预备知识

在证明主要结果之前，我们先了解一些证明中用到的概念.

设Q为含有h个八边形的八边形链，则其中的八边形有以下四种联接方式：每个八边形链都有两个起止八边形l1,而其他的八边形为直线型的l2，拐角型的a或s.如图2中所示.

由于本质上l1和l2并无分别，故均用l来表示.因此，含有h个八边形的八边形链Q可以用一系列关于1,a和s的字母序列来表示，称此序列为las-序列.例如：图1中的八边形链所对应的las-序列为：llslaslll,我们将ll和lll分别简记为l2和l3等等，则图1中八边形链的las-序列可简记为：l2sl1al0sl3.八边形链的las-序列的一般形式为：lt1Plt2Plt3…ltn-1Pltn，其中，P为拐角八边形s或a.

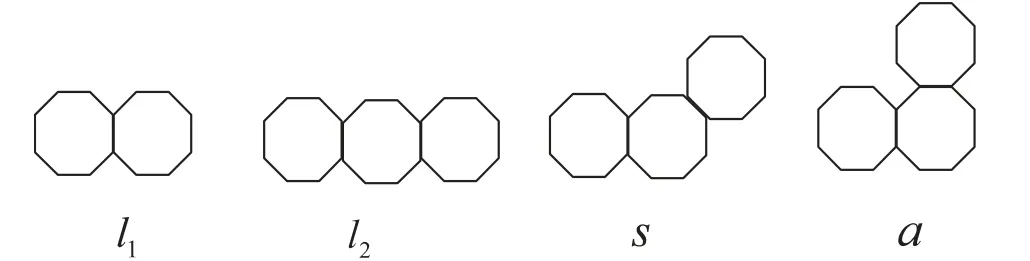
图2

在六边形链中，六边形的联接主要有三种联接方式：起止六边形L1，直线型六边形L2,拐角六边形A，如图3所示.从而，对于任意一个六边形链H，都存在一个与之相对应的LA-序列，且它的一般形式为：Lt1ALt2A…Ltn-1ALtn.

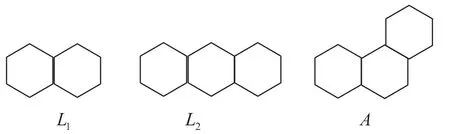
图3

下面我们介绍一类Caterpillar树：设Pn为n个顶点的路，树T(t1,t2,…,tn)为将tj个顶点联接到Pn上第j(j=1,2,…，n)个点得到的图.例如，T4和T(2,1,0,0,1)如图4所示.

下面我们介绍八边形链中一种新的变换：

2.1 变换C

对于八边形链中任意一个八边形(a1,a2,a3,…,a8),都存在两个度数为2的相邻的顶点ai,ai+1，去掉以ai,ai+1及它们相关联的边，再连接ai-1与ai+2，得到六边形(a1,…,ai-1,ai+2,…,a8).称此为变换C，我们对每一个八边形都实行这种变换则得到一个新的六边形链.

引理2.2[4]对于任意六边形链H，H的LA-序列为Lt1ALt2A…Ltn-1ALtn，则H中的Kekulé 结构总数与Caterpillar树T(t1,t2,…,tn)的Hosoya指标相等.

引理2.3[5]对于任意LA-序列为Lt1ALt2A…Ltn-1ALtn的六边形链H，有

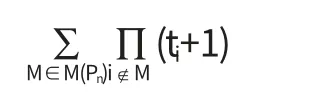
其中，M为路Pn的一个匹配，M(Pn)为路Pn的所有匹配的集合，从而有|M(Pn)|=Z(Pn).

3 主要结果的证明

定理3.1 对八边形链Q的每个八边形施行C变换得到六边形链H，则有Q的完美匹配数与H的完美匹配数相等，即K(Q)=K(H).

证明 设八边形链Q的lax-序列为…lt1Piltn+1…，其中Pi(i=1,2,…,n)为Q中的第i个八边形，Pi中四个相继的顶点记为wi,xi,yi,zi，其中，d(xi)=d(yi)=2，则对这四个点施行C变换，即去掉Pi的顶点xi与yi以及边xiyi,wixi,yizi，再连接wizi.对于Q中任意一个完美匹配M，若xiyi∈M，则对应六边形链H中的不包含wizi边的完美匹配；若xiyi埸M，则对应H中包含边wizi的完美匹配.从而得到，Q中完美匹配的数目与H中完美匹配数目的相等.

定理3.2 对于lsa-序列为lt1Plt2Plt3…ltn-1Pltn，其中P为拐角八边形a或s，存在与之相对应的Caterpillar树T(k1,k2,…,kq)，其中q-1为八边形链中l2与a的个数之和.

证明 不难看出，我们在对八边形链Q施C 变换的过程中，有如下对应关系：l1→L;l2→A;a→A;s→L，这样我们得到一个与八边形链相对应的LA-序列，且在这个序列中A的个数为lsa-序列中l个数与a的个数之和减2，定理得证.

至此，我们证明了对于任意的八边形链A，我们很快能找到与之相对应的Caterpillar树T(k1,k2,…,kq)使得K(Q)=Z(T(k1,k2,…,kq)).

同理，对于任意n边形链Q(n≥8且n为偶数)，我们可反复使用C变换可得到与这个多边形链对应的一条六边形链P，且在这个变换过程中Kekulé 的结构数目不变，再利用引理2.2可得到存在Caterpillar树T(k1,k2,…,kq)，并且n边形链中Kekulé 的结构数目与T(k1,k2,…,kq)的Hosoya指标相等，即K(Q)=Z(T(k1,k2,…,kq)).

〔1〕Hosoya H.Topological index. A newly proposed quantity characterizing the topo-logical nature of structural isomers of saturated hydrocarbons, Bull. Chem. Soc. Jpn.44 (1971) 2332-2339.

〔2〕Gutman, I.: Extremal hexagonal chains. J. Math. Chem.12 (1–4), 197–210 (1993). Applied graph theory and discrete mathematics in chemistry (Saskatoon, SK, 1991).

〔3〕Zhang, L.-Z.: The proof of Gutman’s conjectures concerning extremal hexagonal chains. J. Syst. Sci. Math.Sci. 18(4), 460–465 (1998).

〔4〕I.Gutman, Topological properties of benzenoid systems,Theor.Chim.Acta. 45 (1977)307-315.

〔5〕H. Hosoya, I. Gutman, Kekulé structures of hexagonal chains -some unusual connections, Math. Chem. 44(2008) 559-68.

〔6〕S.L.Li, W.G.Yan,Kekulé structures of polyomino chains and the Hosoya index of caterpillar trees, Discrete Math. 312(2012) 2397-2400.