基于样本空间排序法的剩余寿命评估

顾华海，刘雨时，吕永佳

（第二炮兵工程学院陕西西安710025）

近些年，随着人们对于CBM维护的重视及智能预诊技术的发展，越来越多的方法被用于面向预诊的寿命预测，国内外常见的有基于时间序列的ARMA模型[1]、神经网络模型[2]、灰色理论模型[3]、马尔可夫模型[4]，贝叶斯网络（Bayesian Network）模型[5]等。ARMA模型只适用于平稳的时间序列，神经网络需要大量的历史数据进行训练，对样本量较小的数据不适用，GM（1，1）灰色理论模型预测效果在很大程度上取决于原始数据的特点，要求时间序列近似呈指数规律变化，或者说要求数据总体上呈单调较平缓变化，马尔可夫模型需要知道事物从一种状态变换到另一种状态的概率，Bayes方法的关键是必须确定有关参数的先验分布，并受先验偏差影响较大。

本文采用样本空间排序法[6]计算可靠性参数的置信限，并进一步建立剩余寿命评估模型。

1 基本概念

1.1 不同定时截尾数据

从某种产品中随机抽取n件进行检测，这n个子样投入贮存的时间不一定相同，观测截止时间也不一定相同。设n个子样从开始贮存至观测点的时间间隔分别是t1，…，tn，观测结果用z1，…，zn表示；当第i件产品在时刻ti观测时发现失效，结果记为zi=0；若发现未失效，结果记为zi=1。此数据称为不同定时截尾数据，表达式为：

1.2 指数分布

若随机变量X的分布函数F（t）满足：

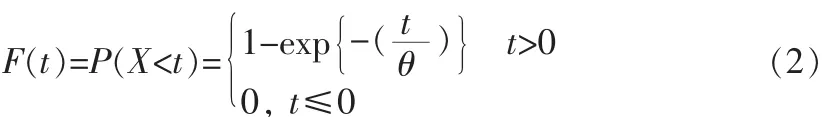
则称X服从指数分布。其中：θ是平均寿命，未知的正数。

1.3 威布尔分布

若随机变量X的分布函数F（t）满足：

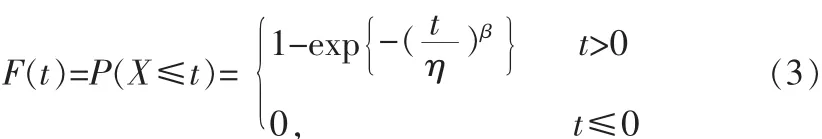
则称X服从威布尔分布。其中：β是形状参数，未知参数；η是刻度参数，未知参数。

2 样本空间排序法

1）在样本空间中，随机向量（z1，…，zn）所可能取的值组成集合E，E={（i1，…，in）:ik=0或1，k=1，2，…，n}，在E中定义次序如下：设x=（x1，x2，…，xn）∈E，y=（x1，y2，…，yn）∈E，若下列条件之一成立：

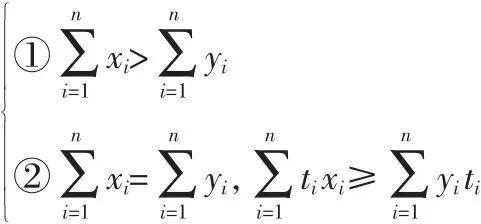
则称x≥y。令，

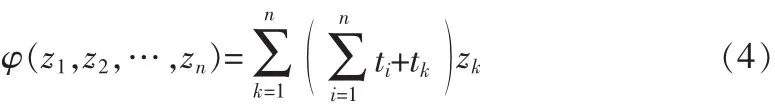
2）设g（θ）是Θ上任一实值函数，给定0＜α＜1，对任何的y∈E，令，

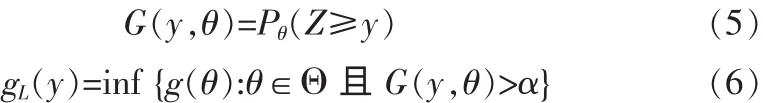
则gL（Z）是g（θ）的1-α置信水平下限，即：

3）gL（Z）是单调的，即若h（z）是g（θ）的任何1-α水平的单调的置信下限，则，

用G（z1，…，zn，θ）表示观测结果（y1，…，yn）不次于给定的（z1，…，zn）的概率。

3 贮存寿命评估模型

3.1 指数分布评估模型

设产品的贮存寿命服从指数分布，n个产品对应的数据（t1，z1），（t2，z2），…，（tn，zn）为不等定时截尾数据。则贮存可靠度为:

指数分布情形下产品的贮存寿命为：

式（10）中：R0是规定的贮存可靠度，θL是θ的估计值。显然求出未知的正数θL，即可得到产品贮存寿命。根据样本数据特征，分以下几种情况讨论：

1）有失效情形

由样本空间排序法理论知，Gn（z，θ）=Pθ（Z≥z），即：

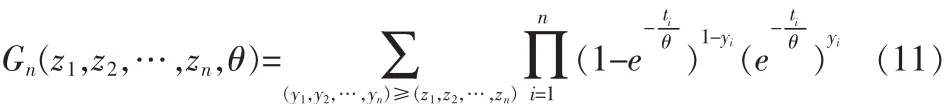
从数学上可以证明，对于一切z≠（0，0，0…），Gn是θ的严格增连续函数，且，

于是对于任何给定0＜α＜1，方程（12）

有唯一根。这个根就是θ的1-α水平置信下限θL。则由式（10）可得产品的贮存寿命TA。

2）零失效情形

当Zi=1时，由式（11）和（12）可得出：

从而有，

将θL代入公式（10）便得到1-α水平的贮存寿命。

3.2 威布尔分布评估理论模型

已知产品的贮存寿命服从威布尔分布，n个产品对应的数据（t1，z1），（t2，z2），…，（tn，zn）为不等定时截尾数据。则贮存可靠度为：

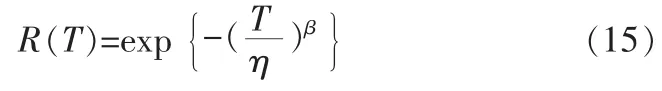
威布尔分布情形下产品的贮存寿命为：

式（16）中：R0是规定的贮存可靠

根据样本数据特征，可分以下几种情况讨论：

本文只讨论数据类型为有失效情形的情况，对于无失效情形这里不做考虑。当zi不恒为1，也不恒为0时，利用样本空间排序法理论可推出1-α水平贮存可靠度置信下限为:

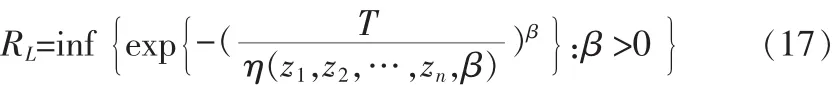
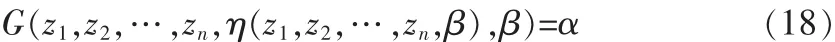
的唯一根。式中G（z1，z2，…，zn，η，β）是η的严格增连续函数。

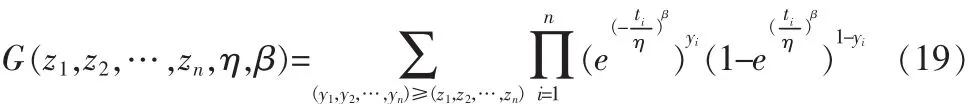
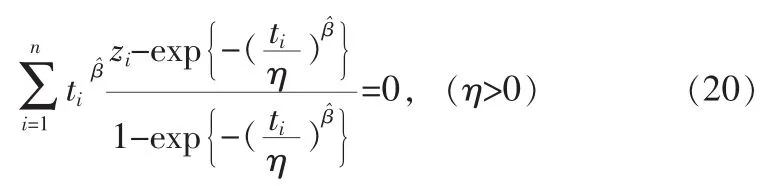
4 实例分析

下面应用样本空间排序法进行模拟计算。模拟数据如下：

表1 指数型产品寿命数据Tab.1Lifetime of one exponential component

采用蒙特卡罗方法仿真威布尔寿命型产品数据如表2所示。

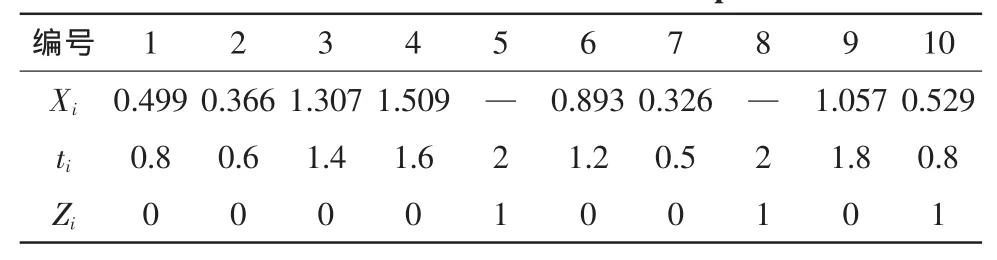
表2 威布尔型产品寿命数据Tab.2Lifetime of one weibull component

由这些数据，用样本空间排序法可计算出β的估计为β^=1.451，带入式（20）可得η^=1.325，则由式（16）得TA=0.471。

5 结论

由以上计算可知，运用样本空间排序法计算指数型和威布尔型产品寿命，计算方法较简洁，误差较小。特别在样本量较少的情况下，运用样本空间排序法也有较好的精度。

[1]YAN Ji-hong，LEE J.A hybrid method for on-line performance assessment and life prediction in drilling operations[C]//ProceedingoftheIEEEInternationalConferenceon Automation and Logistics，Jinan，China，2007:2501-2505.

[2]HUANG Run-qing，XI Li-feng.Residual life predictions for ballbearingsbasedonself-organizingmapandback propagation neural network methods[J].Mechanical Systems and Signal Processing，2007（21）:193-207.

[3]LIU Pan，GENG Gang-qiang.Life prediction on protective coating of steel bridge based on gray system theory[C]//Proceedings of 2007 IEEE International Conference on Grey SystemsandIntelligentServices，NanjingChina，2007:712-716.

[4]Rowatt J D，Spanos P D.Markov chain models for life prediction of composite laminates[J].Structural Safety，1998（20）:117-135.

[5]杨军，赵宇，李学京，等.复杂系统平均剩余寿命综合评估方法[J].航空学报，2007，28（6）:1351-1354.YANGJun，ZHAOYu，LIXue-jing，etal.Comprehensive evaluation of mean residual life of complex system[J].Acta Aeronautica Et Astronautica Sinica，2007，28（6）:1351-1354.

[6]李庆华.威布尔分布下不同定时截尾数据的可靠度的置信下限[J].西安邮电学院学报，2008，13（5）:158-161.LI Qing-hua.The lower confidence limit of reliability of the data with varying censored time under Weibull distribution[J].Journal of Xi’an University of Post and Telecommunications，2008，13（5）:158-161.