观测迭代的插值滤波算法

张卫华 陈茂树 刘邹 王国栋

1山东理工职业学院机电工程系 山东 272100

2中国矿业大学信息与电气工程学院 江苏 221000

3山东兖矿集团 山东 273500

0 前言

虽然卡尔曼滤波器(KF)能够很好的处理线性滤波问题。然而在现实世界中我们所面对的问题大多是非线性问题。为解决非线性滤波问题，众多学者进行了大量的研究并取得了不少的成果。在众多研究成果中较为典型的算法有扩展卡尔曼滤波器(Extended Kalman filter)，Unscented卡尔曼滤波(Unscented Kalman filter)，基于 Bayes理论的粒子滤波器(Particle filter)，和基于Stirling,s内插公式的插值滤波器(DDF)。

EKF简单容易实现特点使其被大量应用到现实工程中，但 EKF实现性差，估计精度差的缺点限制了其进一步的应用。PF算法虽然有着较高的跟踪精度但其庞大的计算量和粒子退化问题限制其在现实工程应用。2000年由 Magnus Nrgaard等人提出的DDF算法，该算法和EKF相类似：算法简单，容易实现。但与EKF相比DDF采用Stirling插值公式进行线性化处理，避免了求解微分应算过程，在非线性程度较高的系统中DDF的跟踪精度要好于EKF。

但标准 DDF算法被应用到初始化误差大或弱观测性条件下的非线性系统，常出现收敛速度慢，稳定性不足及跟踪精度低等问题。为此本文对一阶 DDF算法上进行改进。在一阶 DDF观测更新过程中加入迭代过程取代近似条件估计用于量测预测数据更新。仿真结果表明该算法在大噪声，及初始误差较大的情况下有着更优的跟踪精度和收敛速度。

1 插值滤波器

考虑如下非线性系统∑:

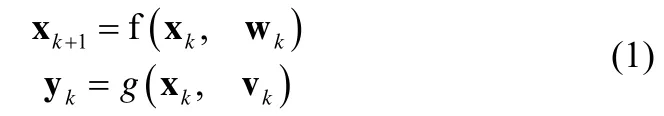
其中 xk∈ℜn为n×1状态向量， yk∈ℜm为m×1观测向量。 wk∈ℜq为q×1过程噪声，而 vk∈ℜr为r×1观测噪声。并假设噪声序列均为高斯白噪声其均值和方差为：

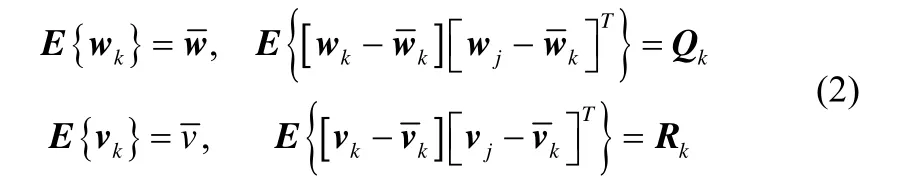
DDF算法和 EKF十分的相似，不同的是 DDF采用Stirling插值公式对系统进行线性化处理而非泰勒公式，从而避免了求解Jacobin矩阵，在状态数据更新上和EKF完全一样，只是在对协方差进行更新的时候可以采取更为简单的方法：通过更新协方差的平方Cholesky因子来完成。DDF算法如下描述：

计算平方Cholesky因子：

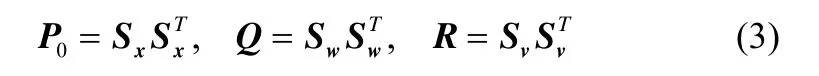
其中Sx为x的协方差P0的平方Cholesky因子，Sw为过程噪声w的协方差Q的平方Cholesky因子，Sv为量测噪声v的协方差R的平方Cholesky因子。

sx,p表示为Sx的第p列，相同的定义其他几个因子则有下面等式：

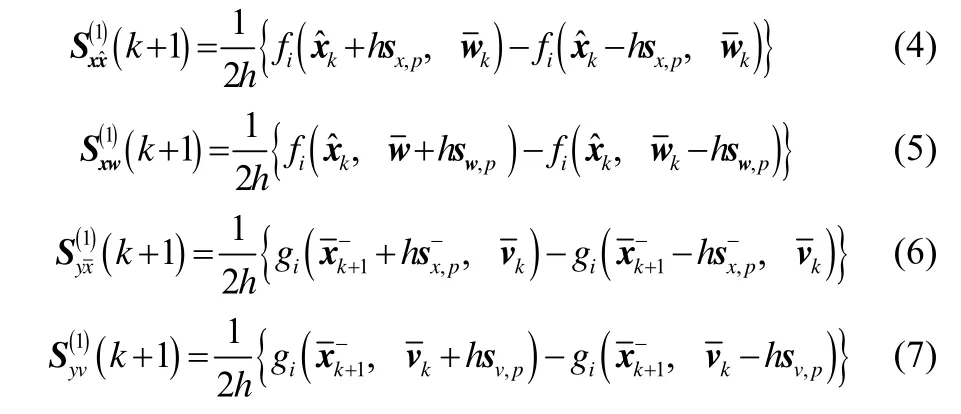
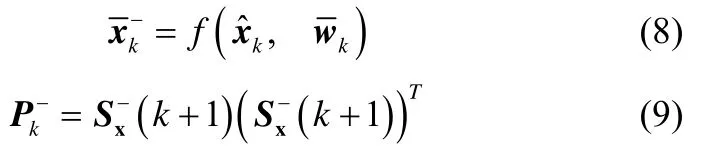
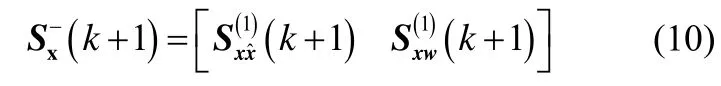
量测数据更新：

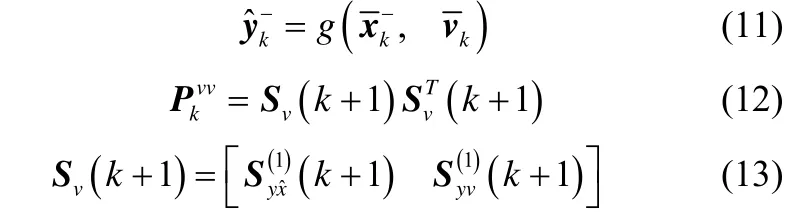
Sv(k+1)也需要进行通过Householder三角变换转换。则量测和状态的相关矩阵为：

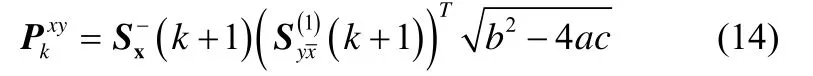
计算增益进行数据更新：

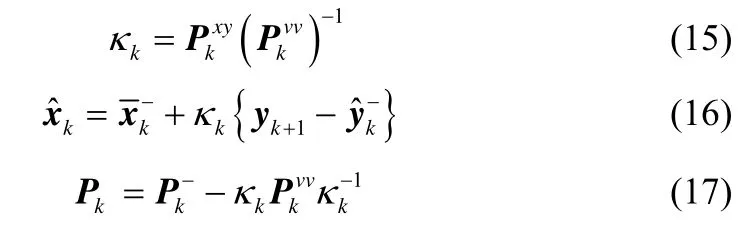
在对协方差更新上注意到式子(9)，(10)，(12)，(13)及(14)之间的关系则在协方差更新中有：

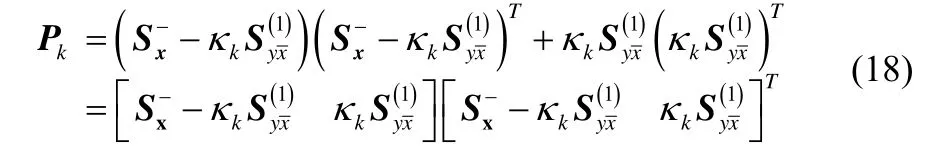
所以使用协方差的平方 Cholesky因子(可以由(19)通过Householder三角变换转换得到)更新来取代协方差进行更新可以简化计算。

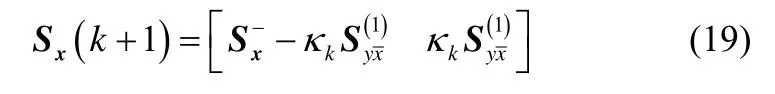
上述即为DDF算法，详细的推导过程可以参见文献。

2 迭代内插滤波器

2.1 观测迭代

为了解决上述问题，本文在观测中加入一个迭代过程来取代单纯的近似条件均值估计，用于代替 x (k)的通过迭代过程不断的逼近 x (k)减小量测预测更新过程的误差，提高算法的鲁棒性及跟踪性能。

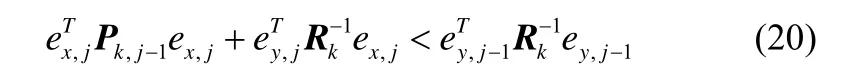
式子中的ey,j和ex,j有如下定义

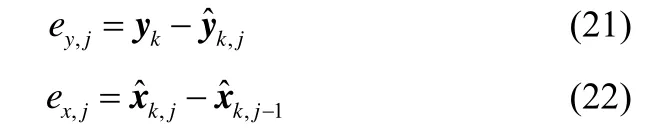
2.2 IDDF算法

本算法和 DDF算法的最大差别在于量测更新，本算法通过迭代环节减小了量测更新的误差具体如下：

假设系统方程为(1)则：

2.计算平方Cholesky因子：

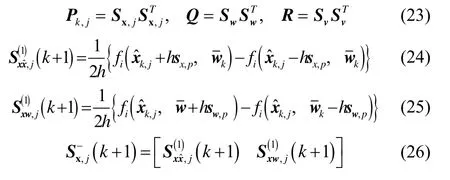
3.状态和协方差计算：

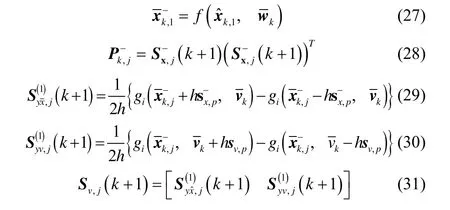
4.量测及相关协方差更新：

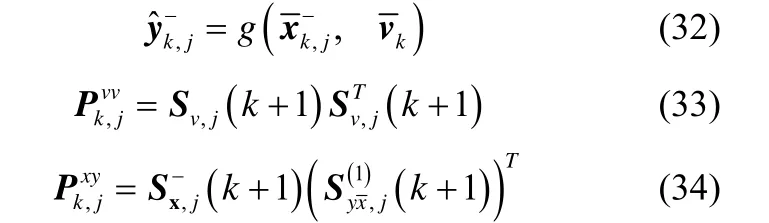
5.计算增益进行数据更新：

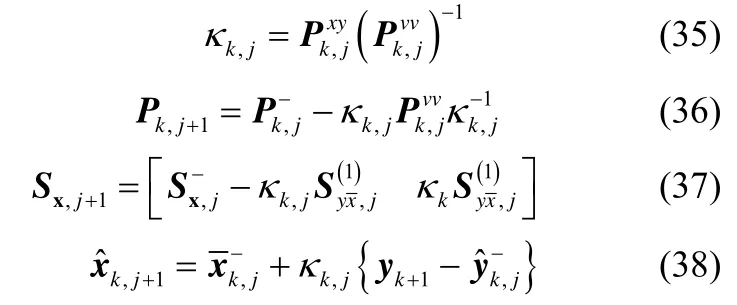
6.定义如下等式：

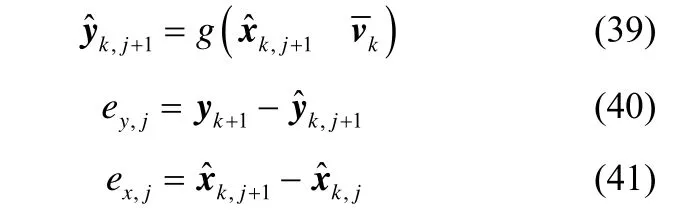
7.判断是否结束迭代：

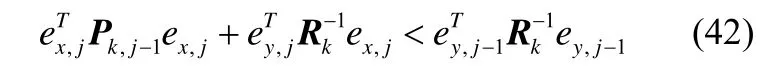
如果 j≤N下不等式成立，则使 j=j+1重复上述算法过程直至不等式不成立或j＞N。

8.数据更新：在上述不等式不成立

当不等式于j＞N依然成立时取：

上述即为 IDDF算法，要注意的是如 Sx,j+1等平方Cholesky因子必须要进行Householder三角变换转换。

2.3 IDDF收敛性

假设

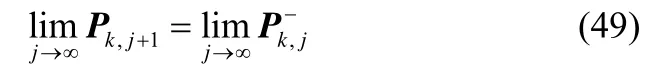
成立。则根据(36)，(48)及(49)可以得到：

成立。与(47)矛盾。所以可知假设(47)不成立(50)成立。

假设 κk,j→ 0当 j＞N时成立，则从(36)及(38)可以知道有：

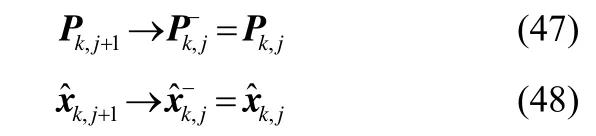
成立，即说明随着迭代过程，算法是收敛的。和标准 DDF算法比较，该算法通过修正量测提高对状态估计的精度，同时在初始化值和最优值相距较远时，算法自动校正状态及协方差矩阵以加快收敛速度。

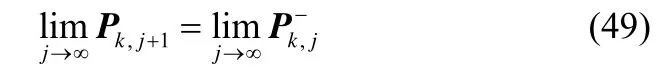
成立。则根据(36)，(48)及(49)可以得到：

成立。与(47)矛盾。所以可知假设(47)不成立(50)成立。

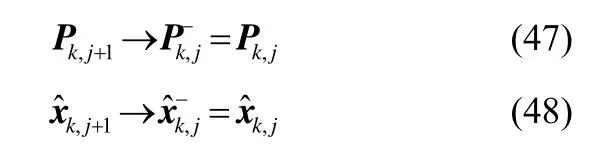
成立，即说明随着迭代过程，算法是收敛的。和标准 DDF算法比较，该算法通过修正量测提高对状态估计的精度，同时在初始化值和最优值相距较远时，算法自动校正状态及协方差矩阵以加快收敛速度。

3 仿真实验

假设如下非线性模型：

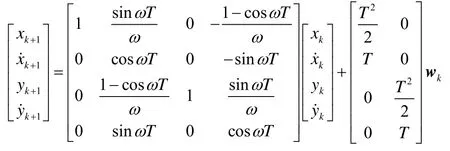
在上述模型中wk为高斯噪声其方差为时间间隔T=0.2s。中的变量分别表示为x方向的位移和速度，y方向的位移和速度。

其中量测包括方向角kθ及方向角变化率量测方程如下：

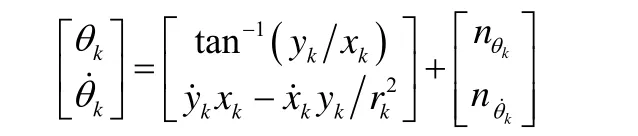
均方根误差为：

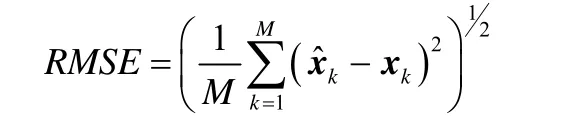
由下述仿真实验数据可以看出IDDF算法在精度和稳定性上的表现都要比DDF和EKF优秀。

4 结论

DDF算法在应对非线性程度高的滤波问题上的不仅在精度上而且在稳定性都要优于EKF。在DDF基础上的改进算法IDDF其精度，稳定性则要好于DDF。IDDF虽然提高了算法的精度及稳定性，但其增加的迭代过程，将加大算法的计算负担。同时对 DDF这中改进算法也只适用于高斯噪声的环境，在面对非高斯噪声环境也是无能为力。

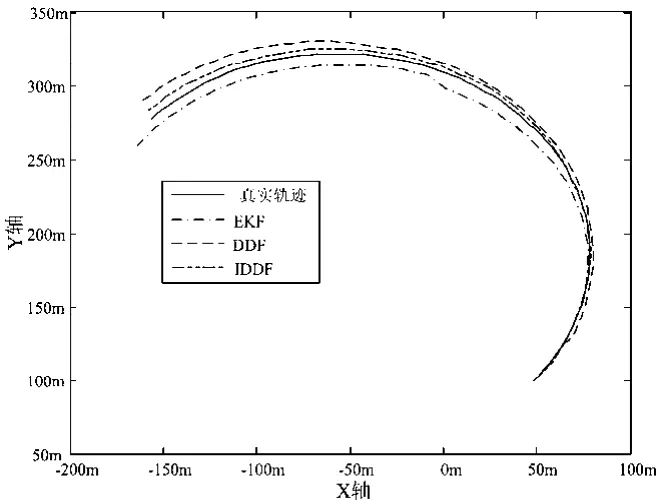
图1 不同非线性滤波算法一次独立仿真跟踪曲线

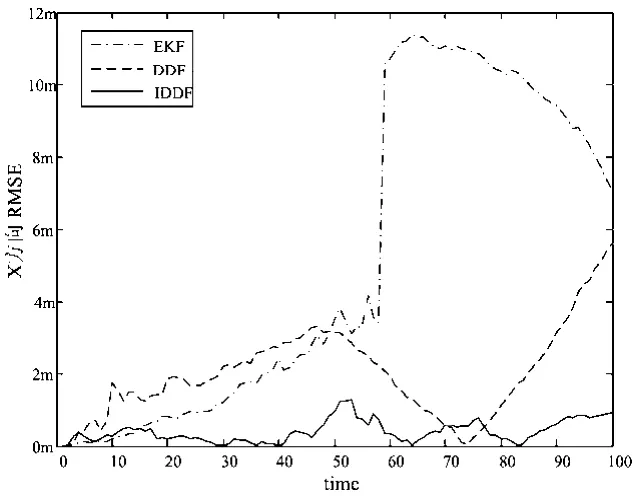
图2 不同滤波算法150次独立仿真x轴方向位移RMSE

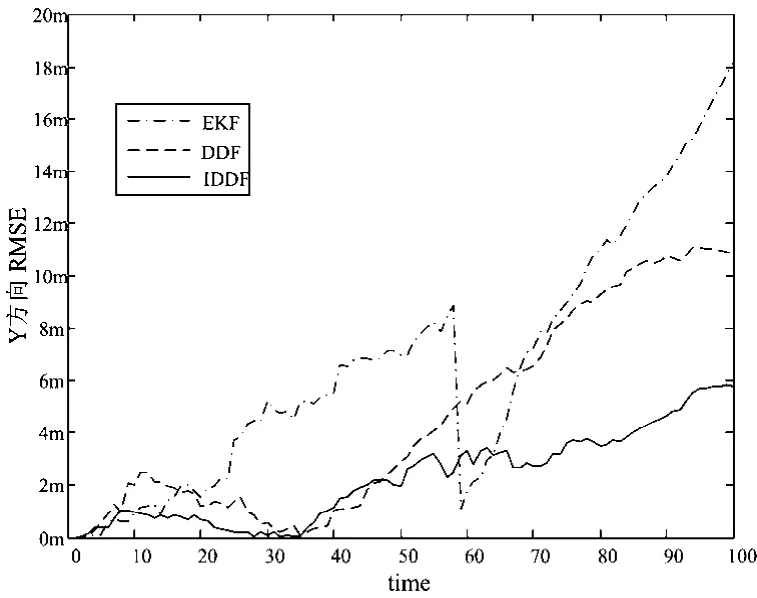
图3 不同滤波算法150次独立仿真y轴方向位移RMSE

[1]Kotecha, J. H, Djuric ,P .M, Gaussian Particle Filtering[J]. IEEE Transactions on Signal Processing.2003.

[2]Julier S J, Uhlmann J K. A New Method for The Nonlinear Transformation of Means and Covariances in Filters and Estimators[J]. IEEE Transactions on Automatic Control, 2000.

[3]Julier S J, Uhlmann J K. Unscented Filtering and Nonlinear Estimation [J]. Proceedings of the IEEE.2004.

[4]袁泽建,郑南宁,贾新春.高斯-厄米特粒子滤波器[J].电子学报.2003.

[5]Nøgarrd M,Poulsen N M, Ravn O.New Developments in State Estimation for Nonlinear System[J].Automatica.2000.

[6]Deok-Jin Lee. Nonlinear Bayesian Filtering with Applications to Estimation and Navigation[D]. Texas A&M University.2005.